Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 38
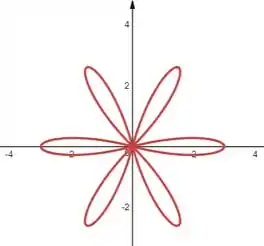
Esboce a curva com a equação dada.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar:
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Queremos esboçar esse gráfico.
Então como faremos isso???
Bom... Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido...
Então vamos colocar alguns valores para e substituir na equação a fim de analisarmos o seu comportamento!! 😉
Passo 2
Primeiramente calculamos valores de para alguns valores de :
Vamos calcular para :
Para :
Para :
Para :
Para :
Passo 3
Agora precisamos saber como a função se comporta entre esses ângulos, para isso vamos analisar a função .
Como o é só uma constante multiplicando, vamos analisar somente o e no gráfico triplicamos todos os valores.
A análise vai ser um pouco complicada, já que temos o como multiplicativo no argumento, teremos que fazer uma análise dando voltas no círculo trigonométrico, uma volta e meia no cosseno por quadrante do plano.
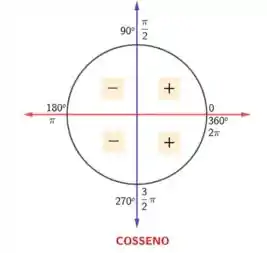
No primeiro quadrante o argumento do cosseno vai variar de a , e em cada quadrante vai ter uma amplitude de , ou seja uma volta e meia na função por quadrante.
Neste intervalo o valor do cosseno vai iniciar em diminuindo para e para , depois subindo para e para retornando ao e finalizando no .
Para o segundo quadrante o argumento vai variar de a e o valor do cosseno vai de ao , depois ao , logo após voltando ao e ao e por fim subindo novamente ao e ao
No terceito quadrante repete o comportamento do primeiro e no quarto repete o do segundo.
Passo 4
Lembrando que o não assume valores negativos, mas pra questão do gráfico podemos assumir os valores negativos de como uma distancia no sentido oposto, ou desconsiderar todos esses valores.
Depois de analisado os valores do cosseno em todo o intervalo, vamos ao plano tentar representar nosso pensamento.
Se nós considerarmos os valores negativos da função como uma distância no sentido oposto, teremos o seguinte gráfico:
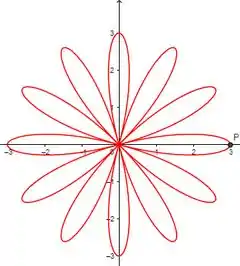
Se desconsiderarmos todos os valores negativos da função, teremos o seguinte gráfico:
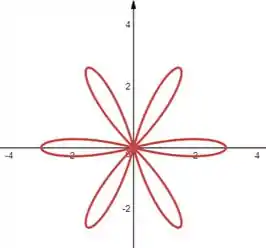
Resposta
