Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 41
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
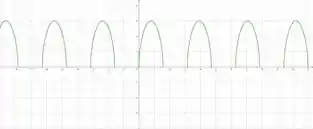
Já para encontrarmos os gráficos no plano polar e no plano cartesiano nós iremos criar uma tabela com diversos pontos para e seu respectivo valor de .
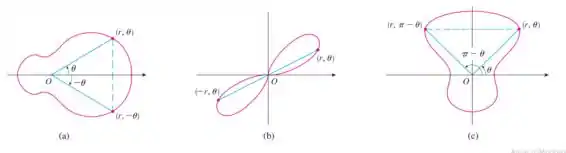
Quando esboçamos curvas polares, às vezes é útil aproveitar a simetria.
- Se uma equação polar não se altera quando é substituído por , a curva é simétrica em relação ao eixo polar.
- Se a equação não se altera quando é substituído por , ou quando é substituído por , a curva é simétrica em relação ao polo. (Isso significa que a curva permanece inalterada se a girarmos em torno da origem.)
- Se a equação não se altera quando é substituído por , a curva é simétrica em relação à linha vertical .
Passo 2
Vamos então a nossa tabela:
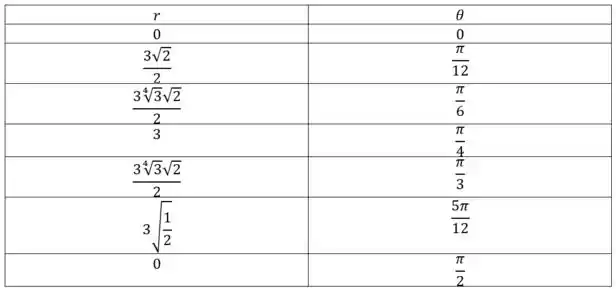
A gente vai ter então como nossa figura:
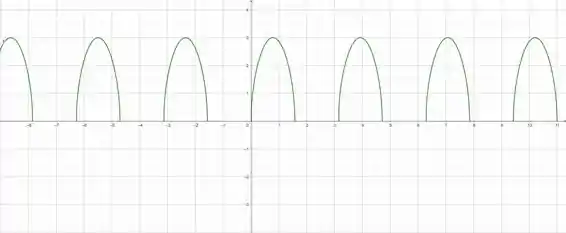
Passo 3
Com essa tabela em mãos vamos fazer os testes do passo 1:
Substituindo por :
Como a função seno ímpar, então o que temos é:
Então a nossa figura não é simétrica em torno do eixo polar.
Vamos para o teste :
Isso não altera o resultado, então nossa figura é simétrica em relação ao polo.
Agora vamos ao teste :
Utilizando a fórmula de subtração de seno de ângulos:
Sendo assim, nossa figura é apenas simétrica em relação ao polo. Abaixo vamos a seu esboço.
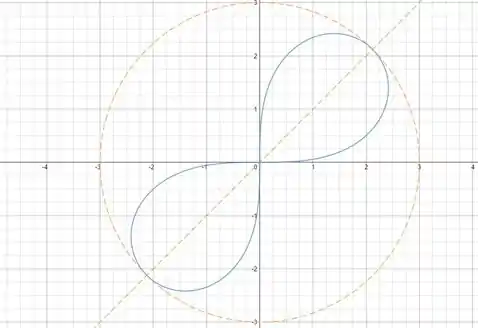
Resposta
