Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.7 - Ex. 22
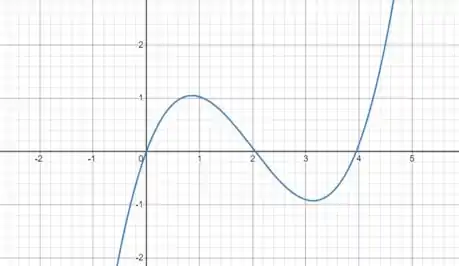
Esboce o gráfico de uma função para a qual
Passo 1
Opa, vamos fazer essa questão! Temos aqui um quebra cabeças. Devemos esboçar um gráfico pra sabendo que:
Vamos dividir esse problema em três partes, os pontos definidos, as derivadas e os limites!
- Na primeira parte a gente só precisa montar os pontos nos gráficos;
- Depois a gente vai pras derivadas, lembrando que é a inclinação da reta tangente da curva no ponto . Pra descobrir a equação das retas tangentes vamos usar a seguinte fórmula geral:
- Os limites eles são do infinito pro infinito, então eles vão servir pra a gente saber da onde a curva tá indo e pra onde ela vai.
Então a gente vai desenhar as retas tangentes pra começar a criar a “silhueta” do gráfico!
Passo 2
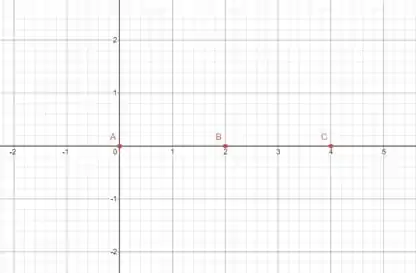
Primeiro vamos focar nos pontos definidos
Vamos então marcar os pontos de :
Passo 3
Temos que que é a inclinação da reta tangente em , o enunciado nos dá as seguintes derivadas:
Podemos tirar daí as equações das retas tangentes, sabendo que a equação de uma reta qualquer pode ser dada por:
Conhecemos , , ), , , ) então podemos substituir pro nosso caso:
Lembrando que :
Agora vamos pra lembrando que :
Finalmente temos e também é igual a zero:
Agora a gente vai desenhar essas retas no gráfico porque elas vão nos ajudar chegar no formato final!
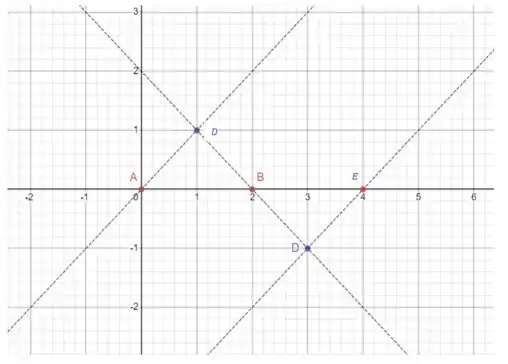
A gente pode perceber que quando a reta tangente tem uma inclinação positiva ela é crescente, portanto é crescente nesse ponto, se a inclinação é negativa será decrescente.
Então analisando o gráfico já podemos deduzir que no ponto a nossa curva vai passar crescendo e em ela vai passar decrescendo, então podemos esperar uma concavidade pra baixo em , onde ocorre a intersecção entre as duas retas tangentes.
Seguindo com o mesmo raciocínio podemos esperar uma concavidade voltada pra cima em .
Passo 4
Agora vamos analisar os limites:
Temos que a função quando tende a menos infinito ela decrescerá, e quando tende a mais infinito ela crescerá. Juntando isso com as reflexões que a gente fez no passo anterior podemos desenhar o seguinte gráfico:
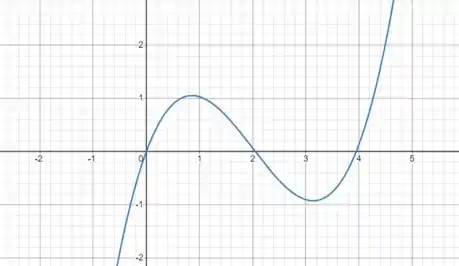
Prontinho!
Resposta
