Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 12
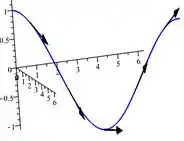
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.
Passo 1
Fala galera. Tudo belezinha?
Vamos começar a resolver a questão!
Primeiro iremos analisar o enunciado. E através da função iremos esboçar o gráfico e mostrar a direção que o parâmetro cresce.
A partir das derivadas iremos substituir diferentes valores de na função e analisar o seu comportamento.
Pois então, mão na massa!
Passo 2
A direção na qual o parâmetro cresce ao longo da curva definida por
podemos usar o conceito de derivadas e vetor tangente à curva. A tangente a uma curva em um ponto específico fornece a direção instantânea da curva naquele ponto.
Vou te mostrar como se faz!
Primeiro, calcule a derivada da função vetorial em relação a . A derivada nos dará o vetor tangente à curva em cada ponto.
Portanto,
Passo 3
Agora que temos a derivada vetorial , podemos usá-la para encontrar a tangente à curva em qualquer ponto específico. Vamos calcular a tangente em alguns pontos-chave:
Para :
Para :
Para :
Analisando as posições, temos que a curva é uma trajetória no espaço tridimensional que oscila em torno do eixo enquanto se move no plano .
A tangente à curva indica a direção instantânea da curva em diferentes pontos. Nas posições e , a tangente é na direção de , enquanto em , a tangente é na direção de .
Passo 4
O gráfico ficará:
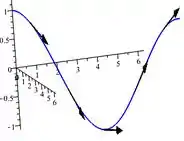
O comportamento do gráfico revela uma curva paramétrica que se estende linearmente nos planos , enquanto exibe oscilações periódicas na direção do eixo . Isso proporciona uma representação visual interessante da relação entre os parâmetros e a forma da curva no espaço tridimensional.
Resposta
