Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 25
- Escreva a integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado.
- Use sua calculadora para determinar a integral com precisão de cinco casas decimais.
em torno do eixo
Passo 1
Opaa! Temos as seguintes curvas:
em torno do eixo
E queremos a integral para o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo dado. Bora fazer um esboço pra ficar mais claro:
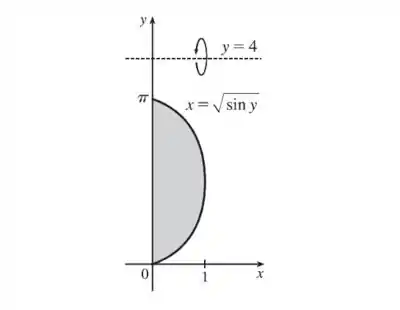
Passo 2
Para calcular o volume do sólido vamos usar a seguinte fórmula:
Onde:
Temos que a altura da curva é dada pela própria função:
Já a circunferência, como não iniciamos a rotação de zero, é dada por Sendo assim:
Passo 3
Agora vamos usar a calculadora para resolver a integral anterior, beleza ?
Resposta
Exercícios de Livros Relacionados
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y 2 = x ,x = 2 y
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo y da região limitada pelas curvas dadas. Esboce a região e uma casca típica. y = 1 x ,y = 0 ,x = 1 ,x = 2
Ache o volume do sólido gerado pela rotação, em torno da reta x = 3 , da região limitada por aquela reta, pelo eixo x e pelo gráfico y = 9 x - x 4 12 .
Use o teorema de Pappus para encontrar o volume de um cone circular reto com 2 m de raio da base 3 m de altura.
Use o teorema de Pappus para encontrar o volume da esfera de raio 4 m.