Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.1 - Ex. 3
Desenha a curva e visualmente estime o comprimento. Depois ache o seu comprimento exato.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui a atividade pede para a gente desenhar a curva e estimar o seu comprimento visualmente e após fazermos isso calcularmos o valor exato utilizando a formula de comprimento de curva.
Inicialmente vamos a curva:
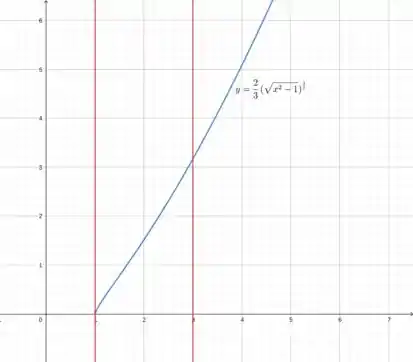
Passo 2
Vamos considerar que a curva seja uma reta e utilizar Pitágoras para estimar o valor:
Agora iremos utilizar a fórmula para encontrarmos o valor exato:
Resposta
Exercícios de Livros Relacionados
Um fabricante de telhados metálicos corrugados quer produzir painéis que tenham 60 cm de largura e 4 cm de espessura processando folhas planas de metal como mostrado na figura. O perfil do telhado tem
O Gateway Arch, em St. Louis, foi construído usando a equação y = 211,49 - 20,96 cosh 0,03291765 x para a curva central do arco, em que x e y estão medidos em metros e x91,20 . Escreve uma integral
Ache o comprimento da curva. y = ln ( 1 - x 2 ) , 0 ≤ x ≤ 1 / 2
Ache o comprimento da curva. 18 .y = ln e x + 1 e x - 1 ,a ≤ x ≤ b ,a0
Trace a curva e estime visualmente seu comprimento. A seguir, encontre seu comprimento exato. y = x 2 + x 3 ,1 ≤ x ≤ 2