Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 30
- Estime o valor de
Traçando o gráfico da função . Forneça sua resposta com precisão de duas casas decimais.
- Verifique sua resposta da parte (a), calculando para valores de que se aproximem de .
Traçando o gráfico da função . Forneça sua resposta com precisão de duas casas decimais.
Passo 1
E aí! como vai?
Nesse problema temos que estimar o valor de
Plotando o gráfico da função do limite e a partir de uma calculadora.
Tem ideia de como fazemos isso?
Essa questão está marcada com o simbolozinho de gráfico, então para resolve-la, vamos ter que recorrer a calculadoras gráficas.
Primeiro vamos plotar o gráfico de e visualizar o valor de .
Depois, com uma calculadora, vamos fazer tendendo a e verificar o valor que a função se aproxima.
Veja só!
Passo 2
Plotando o gráfico de , temos o resultado abaixo
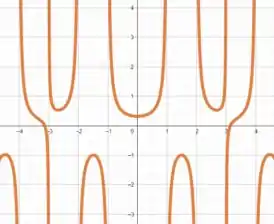
Dando um zoom nele, obtemos:
Logo, verfica-se que, pelo gráfico
Tranquilo até aqui?
Passo 3
Agora, para verificar o resultado obtido em (a), pegamos valores próximos de zero para e aplicamos na função com uma calculadora.
Obtemos assim o seguinte resultado tabelado abaixo:
Isso nos mostra que é válida a resposta obtida em (a) .
E aí! entendeu tudo? Responde Aí!