Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.7 - Ex. 16

Nos exercícios de 13 a 16 , ache a área de intersecção das regiões limitadas pelos gráficos das duas equações dadas.

r ² = 2 cos ⁡ θ r = 1

Passo 1

O enunciado nos da a equação de um gráfico e pede para determinarmos a área. Para isso, primeiro é ideal fazer o esboço do gráfico da equação dada para observar os pontos de intersecção das duas curvas bem como, quais são os limites de θ . Após fazer o esboço da equação , podemos utilizar o que foi mostrado ao longo da seção quando queremos saber a área de uma região dada em coordenadas polares, que nos diz que para calcular a mesma podemos utilizar que a área da região é : A = 1 2 . ∫ α β f θ 2 d θ .

Em muitos problemas também podemos utilizar o conceito de simetria.

Passo 2

Assim, o esboço do gráfico da equação dada é:

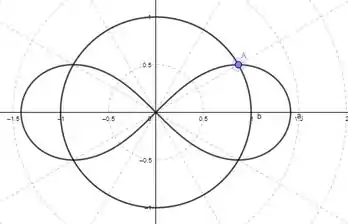
A Primeira região de intersecção é limitada por uma curva com θ indo de 0   a t é π 6 e por outra curva como θ indo de π 6   a t é   π 4 . Sendo assim, a área de intersecção pode ser calculada levando em conta essas variações do ângulo e multiplicada por 4, que é a quantidade de vezes que a região se repete.

Passo 3

Sendo assim, a área é:

A = 1 2 . ∫ α β f θ 2 d θ = 4 . [ 1 2 ∫ 0 π 6 1 2 d θ + 1 2 ∫ π 6 π 4 2 c o s 2 θ d θ ] =

2 ∫ 0 π 6 1 d θ + 4 ∫ π 6 π 4 cos ⁡ 2 θ d θ ] = 2 θ 0 π 6 + 4 1 2 s e n 2 θ π 6 π 4 = 2 π 6 + 2 1 - 3 2 = π 3 + 2 - 3

Resposta

A = π 3 + 2 - 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a equação polar r = a sen ⁡ θ + b cos ⁡ θ , para a qual a b ≠ 0 , representa um círculo e calcule seu centro e raio.
Mostre que as curvas r = a sen ⁡ θ e r = a cos ⁡ θ se interceptam com ângulos retos.
Se a e b forem números fixos, encontre equações paramétricas para a curva que consiste de todas as posições possíveis do ponto P na figura, usando o ângulo θ como parâmetro. Então elimite o parâmetro
Se a e b forem números fixos, encontre equações paramétricas para a curva que consiste de todas as posições possíveis do ponto P na figura, usando o ângulo θ como parâmetro. Então elimite o parâmetro
Encontre as equações paramétricas para o conjunto de todos os pontos P , como mostrado na figura, tais que O P = A B . Esboce a curva. (Essa curva é chamada cissoide de Diocles, em homenagem ao estudi