Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.3 - Ex. 19
Nos exercícios 18 a 23, encontre uma equação da superfície de revolução gerada pela rotação da curva plana dada em torno do eixo indicado. Faca um esboço da superfície
19.
No plano ZY, em torno do eixo z
Passo 1
Oiii a todos que estão ingressando no mundo do cálculo de várias variáveis. Quando aprendemos a fazer gráficos em cálculo 1, aprendemos vários truques. Inclusive, se você já está mais sagaz, de olhar para uma função e concluir “ah isso aqui, tem um jeito de círculo”, por exemplo, rs. Se você ainda não pegou essa sagacidade, relaxe! Isso vem apenas com o tempo e após vários exercícios.
Uma dica que dou é usar muito uma calculadora gráfica. Isso ajuda absurdamente na compreensão da geometria do seu sistema.
Passo 2
No nosso caso temos
Que é uma parábola no plano ZY ,
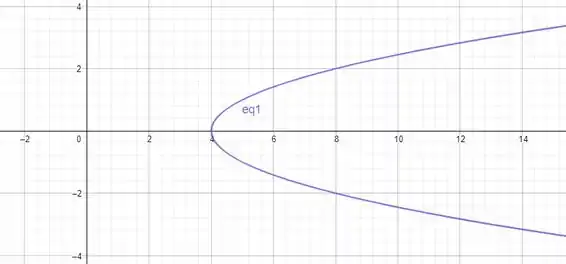
Agora precisamos fazer uma superfície de revolução, uma dica pratica é fazer o seguinte
O que no nosso caso temos essa equação em 2D
E podemos alterar para ter uma revolução em 3D
E se olharmos para o gráfico dessa função percebemos que acertamos
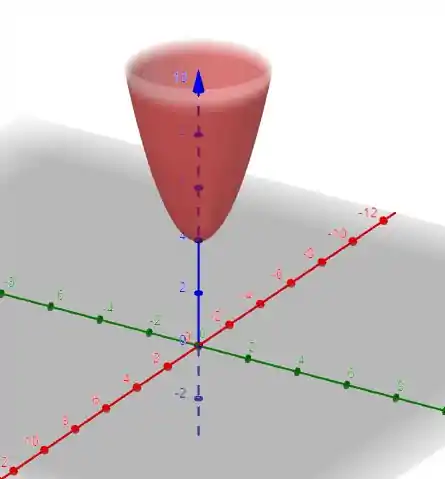
Terminamos por aqui. Te vejo na próxima resolução
: )