Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 26
Um fabricante, ao comprar caixas de embalagens retangulares exige que o comprimento de cada caixa seja e o volume . Para gastar a menor quantidade de material possível na fabricação de caixas, quais devem ser suas dimensões.
Passo 1
Pra começar, vamos fazer uma ilustração do que ele está nos dizendo. Olha só:
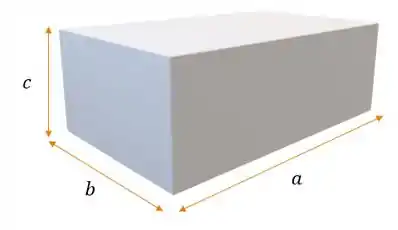
Como o volume da caixa é de :
Como o comprimento de cada caixa deve ser :
Voltando em :
Como queremos usar a menor quantidade de material, a ideia será minimizar a área total. Então vamos ver como fica
Passo 2
Agora vamos derivar e igualar a zero para ver quais são os pontos críticos.
Derivando,
Igualando a zero:
Assim,
Simplificando,
Opa, agora que já sabemos basta voltarmos em e acharmos .
Portanto,
Resposta
Exercícios de Livros Relacionados
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. f
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos exemplos 3 e 4 dessa seção. Faça um esboço do gráfico da função no intervalo. f x = x
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos exemplos 3 e 4 dessa seção. Faça um esboço do gráfico da função no intervalo. g x = x
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. h
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. g