Faça uma correspondente entre a equação e seu gráfico (identificado por -). Justifique sua escolha.
Passo 1
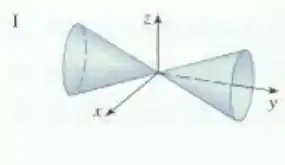
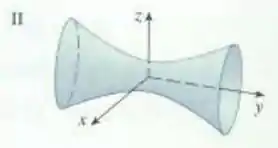
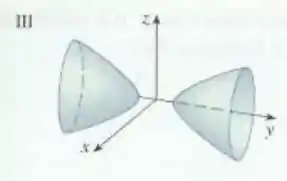
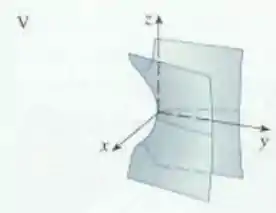
Beleza, pessoal? Perceba que a equação se parece com:
que seria a equação do hiperboloide de duas folhas. Porém, comparando,
vemos que a diferença entre as duas é que o sinal positivo passou a acompanhar , o que significa que o eixo do hiperboloide passa a ser o eixo , ok? Então o gráfico correspondente é:
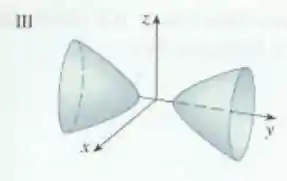
Resposta
Gráfico