Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 50

Faça um gráfico com vários membros das famílias de curvas x = s e n   t + s e n   n t , y = c o s   t + c o s   n t , onde n é um número inteiro positivo. Quais as características que essas curvas têm em comum? O que acontece quando n cresce?

Passo 1

Olá, meu nobre amigo. Vou te ajudar a resolver essa atividade.

A gente tem as famílias de curva parametrizadas:

x = s e n   t + s e n   n t

y = c o s   t + c o s   n t

E queremos entender o comportamento dessas curvas para diferentes valores de n .

Para resolvermos essa atividade, iremos utilizar um software gráfico, eu irei utilizar o GeoGebra, você pode me acompanhar nessa escolha ou pode utilizar o seu software gráfico favorito.

Para esboçarmos as curvas precisamos primeiramente da expressão geral para os membros das famílias das curvas. Vamos fazer isso relacionando x e y em apenas uma equação.

Passo 2

Essa expressão é dada por:

x 2 + y 2 = s e n   t + s e n   n t 2 + ( cos ⁡ t + cos ⁡ n t ) ²

Calculando os produtos notáveis:

x 2 + y 2 = s e n 2 t + 2   s e n   t ∙ s e n   n t + s e n 2 n t + c o s 2 t + 2 cos ⁡ t ∙ cos ⁡ n t + c o s ² n t

Podemos usar as seguintes relações trigonométricas:

s e n 2 A + c o s 2 A = 1

E

cos ⁡ A - B =   s e n   A ∙ s e n   B + cos ⁡ A ∙ cos ⁡ B

desta forma:

x 2 + y 2 = s e n 2 t + c o s 2 t + s e n 2 n t + c o s 2 n t + 2 (   s e n   t ∙ s e n   n t + cos ⁡ t ∙ cos ⁡ n t )

Simplificando utilizando as identidades trigonométricas:

sin 2 ⁡ t + cos 2 ⁡ t = 1

x 2 + y 2 = 1 + 1 + 2 cos ⁡ t - n t

x 2 + y 2 = 2 + 2 c o s ⁡ [ t 1 - n ]

Passo 3

Com a equação da curva em mãos, poderemos criar seus gráficos e entender o comportamento da figura:

Quando n = 1 , x 2 + y 2 = 4 :

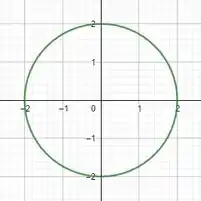
Quando n = 2 , x 2 + y 2 = 2 + 2 cos ⁡ ( - t ) :

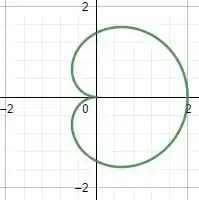
Quando n = 3 , x 2 + y 2 = 2 + 2 cos ⁡ ( - 2 t ) :

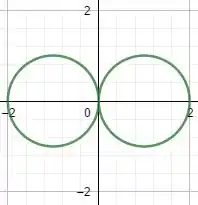
Quando n = 4 , x 2 + y 2 = 2 + 2 cos ⁡ ( - 3 t )

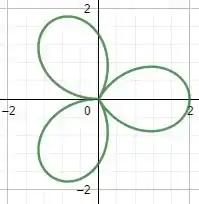
Passo 4

As características em comum das curvas são os loops e o mesmo intervalo de espaço no qual estes loops estão (uma quadrada 2 por 2), e conforme n cresce o número de loops aumenta.

Para sabermos quantos loops terá o gráfico podemos olhar o argumento do cosseno onde temos ( 1 - n ) .

Por exemplo se tivéssemos n=10, teríamos 9 loops.

Resposta

Quando n = 5 , existem 4 formas semelhantes a feijões. O número dessas formas parece ser n - 1 em geral.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a curva com a equação dada. r = 3 cos ⁡ 6 θ
A figura mostra o gráfico de r como uma função de θ em coordenadas cartesianas. Use-o para esboçar a curva polar correspondente.
A partir da Figura 19 parece que a limaçon perde sua covinha quando c = 1 2 . Demonstre isto.
A figura mostra o gráfico de r como uma função de θ em coordenadas cartesianas. Use-o para esboçar a curva polar correspondente.
No Exemplo 11 os gráficos sugerem que a limaçon r = 1 + c sen ⁡ θ tem um laço interno quando c1 . Demonstre que isso é verdadeiro e encontre os valores de θ que correspondam ao laço interno.