Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.6 - Ex. 66

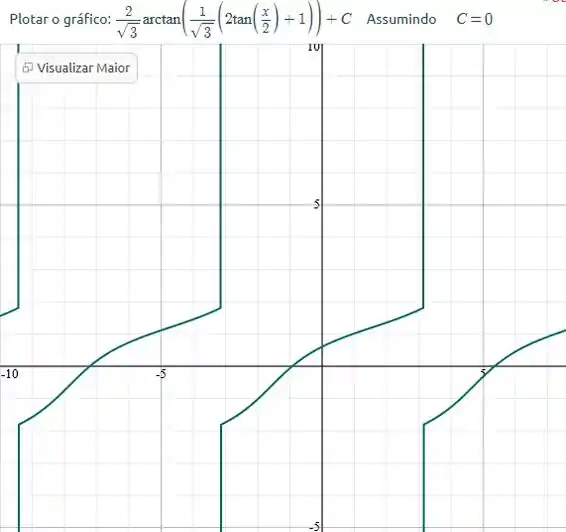
Faça uma substituição u dada por (5) para converter o integrando em uma função racional de u e, então, calcule a integral. (b) Se o leitor dispuser de um CAS, use-o para calcular a integral (sem usar substituições) e, então, confirme que o resultado é equivalente de (a).

∫ 1 2 + sen ⁡ x d x

Passo 1

Usaremos como substituição:

u = tg ⁡ x 2

sen ⁡ x   = 2 u 1 + u 2

d x = 2 1 + u 2 d u  

Portanto:

∫ 1 2 + sen ⁡ x d x = ∫ 2 1 + u 2 d u   2 + 2 u 1 + u 2 = ∫ 2 2 + 2 u 2 + 2 u d u = ∫ 1 1 + u 2 + u d u

Reescreveremos como:

∫ 1 2 + sen ⁡ x d x = ∫ 1 ( u 2 + u + 1 / 4 ) + 3 / 4   d u

Então:

∫ 1 2 + sen ⁡ x d x = ∫ 1 u + 1 2 2 + 3 2 2   d u

Podemos chamar :

t = u + 1 / 2

d t = d u

a = 3 2 2

Aplicando a substituição:

∫ 1 u + 1 2 2 + 3 2 2   d u = ∫ 1 t 2 + a 2   d t

Resolvendo:

∫ 1 t 2 + a 2   d t = 1 a arc tg ⁡ t a + C

Então:

∫ 1 u + 1 2 2 + 3 2 2   d u = 1 3 2 arc tg ⁡ u + 1 2 3 2 + C

Simplificando:

∫ 1 u + 1 2 2 + 3 2 2   d u = 2 3 arc tg ⁡ 2 3 u + 1 2 + C

Substituindo u = tg ⁡ x 2 :

∫ 1 2 + sen ⁡ x d x = 2 3 arc tg ⁡ 2 3 tg ⁡ x 2 + 1 2 + C

Passo 2

Utilizando um CAS:

Resposta

∫ 1 2 + sen ⁡ x d x = 2 3 arc   tg ⁡ 2 3 tg ⁡ x 2 + 1 2 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a integral indefinida geral. ∫ z 2 z 3 + 1 d z
Calcule a integral indefinida. ∫ 5 t sen ⁡ 5 t d t
Encontre a integral indefinida geral. ∫ cos 4 ⁡ θ sen ⁡ θd θ
Encontre a integral indefinida geral. ∫sec 2 ⁡ θ t g 3 θd θ
Encontre a integral indefinida geral. ∫ln ⁡ x2 x d x