Uma família de curvas é dada pelas equações
Onde é um número real e é um número inteiro positivo. Como o gráfico muda quando aumenta? Como ele muda quando varia? Ilustre traçando com uma ferramenta gráfica membros suficientes da família para justificar suas conclusões.
Passo 1
Como temos duas variáveis para controlar, vamos fixar uma enquanto a gente mexe na outra pra gente investigar o comportamento de uma de cada vez, beleza?
Primeiro vamos fixar e fazer variar.
- :
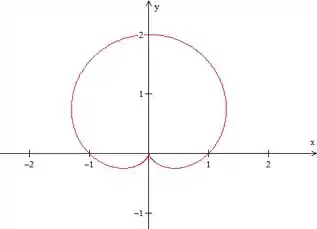
A curva parece que tá querendo dar um looping mas não deu ainda... vamos aumentar o .
- :
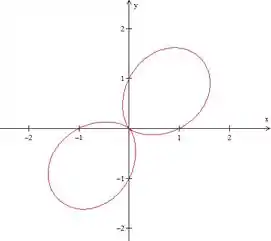
Opa, o que aconteceu foi que a curva se fechou alí no meio, dando um looping e meio que formando duas “pétalas”.
- :
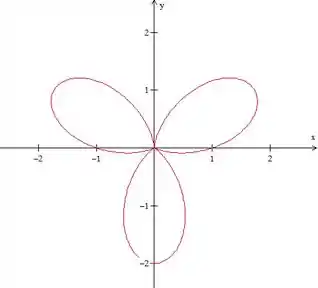
Mais um looping, mais uma “pétala”.
- :
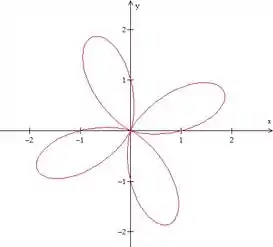
Outro looping, outra “pétala”. Agora parece uma florizinha!! Rsrs
Então quer dizer, parece que quando maior o valor de , mais loopings nossa curva dá.
Passo 2
Agora vamos investigar a influência do .
Para isso, vamos fixar , por exemplo.
Para , já sabemos a cara que a curva tem, pois já desenhamos aí em cima.
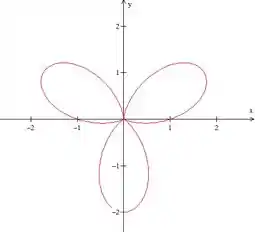
Agora vamos testar outros valores de , que é um número real e, portanto, pode ser negativo também.
- :
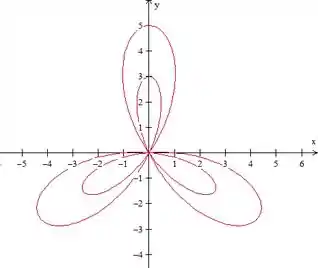
O que aconteceu foi que agora temos duas “flores” de três “pétalas” toda a curva aumentou de tamanho (repare que a escala desse gráfico é menor que quando ).
-
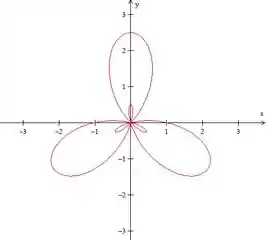
De novo, temos duas “flores” e nossa curva diminuiu de tamanho (essa escala é maior que a anterior), inclusive, o looping de dentro diminui mais que o de fora.
- :
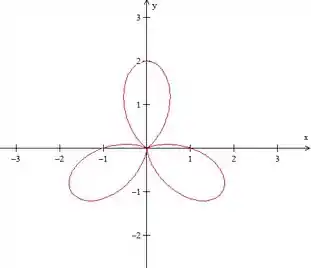
O mesmo comportamento continuou sendo observado: a curva como um todo diminuiu de tamanho e o looping de dentro diminuiu mais que o de fora, tanto que chegou a desaparecer.
Ou seja, para o comportamento da curva é esse de ela ir diminuindo a medida que aumenta, sendo que o looping de dentro diminui mais que o de fora.
Passo 3
Agora vamos ver o que acontece para outros valores de .
- :
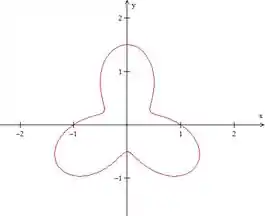
A curva passou a ser uma curva fechada, sem looping. E repare que ela ainda está diminuindo de tamanho.
- :
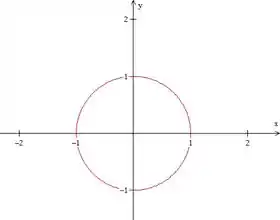
A curva também é fechada e é simplesmente uma circunferência de .
- :
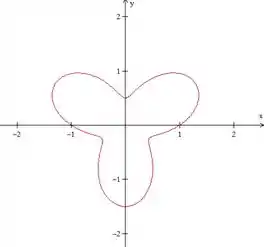
Curva fechada.
- :
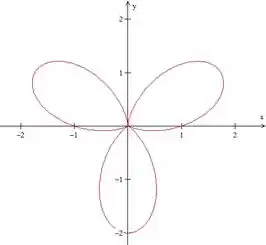
A curva fechou de novo e voltou a fazer loopings.
- :
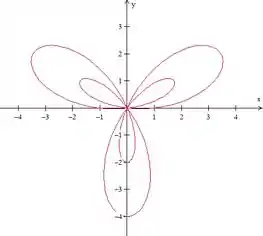
Ou seja, para observamos o mesmo comportamento que para , só que no sentido contrário. Se antes ela diminuía, agora, ela aumenta.
Resposta
Ei, a resposta está no passo a passo :)