Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.7 - Ex. 18
18. Um fazendeiro quer uma cerca em um lote retangular de terra adjacente á parede norte de seu celeiro. Nenhuma cerca é necessária ao longo do celeiro e a cerca ao longo do lado oeste do lote é compartilhada com um vizinho que vai dividir o custo daquela parte da cerca. Se a cerca custa $ 30 por metro linear para instalar e o fazendeiro não está disposto a gastar mais do que $ 1.800, encontre as dimensões do lote que englobaria a maior área.
Passo 1
Opa! Bora pra mais uma questão?! Aqui a gente tem um probleminha:
Um fazendeiro quer cercar um lote retangular adjacente à parede norte de seu celeiro. A cerca só é necessária nos lados leste e sul, pois o lado oeste é compartilhado com um vizinho. O custo de instalação da cerca é por metro linear e o fazendeiro tem um orçamento máximo de .
Sabendo disso a gente tem que encontrar as dimensões do lote que englobaria a maior área com o custo limite de !
Antes de qualquer coisa vamos desenhar pra ficar mais claro:
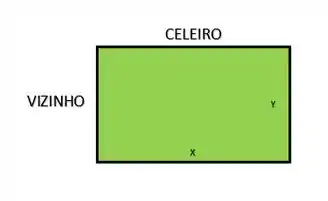
Precisamos de uma função que relacione os lados e a área do terreno com o custo de . Depois vamos usar derivada para calcular a área máxima!
Passo 2
Temos um orçamento de e o metro da cerca custa , vamos calcular quantos metros podemos comprar com o nosso orçamento:
Temos o comprimento de cerca que vamos comprar, então podemos dizer que:
A área do terreno pode ser dada por:
Substituindo:
Passo 3
Para achar a área máxima precisamos derivar a função que encontramos e igualala a zero:
Igualando a zero:
Substituindo na fórmula da área:
Agora só falta calcular o :