Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.5 - Ex. 90
Se for contínua em , demonstre que
Para o caso onde , faça um diagrama para interpretar geometricamente essa equação como uma igualdade de áreas.
Passo 1
Temos aqui um probleminha de demonstração! Temos que provar que:
Pra isso vamos partir da integral da esquerda e usar a substituição:
E vamos provar que com isso chegamos a integral da direita!
A Regra da Substituição nos ajuda a transformar a integral para uma forma mais conveniente, mudando a variável de integração e ajustando os limites de integração.
E seguimos como a substituição normal, calculamos , e depois também calculamos os novos limites devido a substituição.
Não vamos precisar calcular nenhuma integral de fato, apenas provar que ambas são iguais!
Agora vamos resolver!
Passo 2
Como conversamos no passo 1, vamos definir como:
Derivando para encontrar :
Precisamos alterar também os limites de integração:
Para :
Para :
Agora substituímos na nossa nova integral:
Temos que:
Então:
Eu sei que são variáveis diferentes, mas é só a forma com que a gente chama a variável! O valor não muda. Seria a mesma coisa da gente, por exemplo, ter as funções:
Uma é em função de e outra de , mas se substituirmos o mesmo valor nelas teremos o mesmo resultado final!
Passo 3
Agora a gente tem que fazer um diagrama, com , que mostre exatamente o que terminamos de falar. Ou seja:
Desenhando:
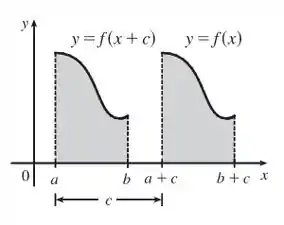
Pelo diagrama, vemos que a equidade se segue do fato de que nós estamos transladando o gráfico de , e os limites de integração, por uma distância .
Ou seja, quando somamos algo nos limites de integração estamos de fato transladando (fazendo a função andar) sobre o !
Resposta
Demonstração.