Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 12.5 - Ex. 11
11)
Passo 1
Analisando a integral, vemos que é interessante quebrar em frações parciais. Mas antes temos que dividir os polinômios para o grau do numerador ficar menor do que o do denominador!!
Fazendo a divisão, as coisas ficam assim:
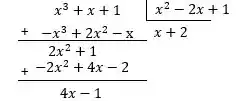
Logo,
Passo 2
Nossa integral era assim:
E vai ficar assim:
Resolvendo a primeira parcela:
Essa segunda é um pouco cascuda, então vamos com calma!
O termo que queremos integrar é o seguinte:
Nesse caso é um pouco diferente, pois temos um termo ao quadrado no denominador! A técnica é assim ó:
Deixando os denominadores iguais:
Fazendo as distributivas:
Voltando para ,
Agora é só comparar os coeficientes do numerador:
De :
Substituindo em :
Logo,
Passo 3
Vamos resolver a
Antes era assim:
E vai ficar assim:
Não esquece:
Agora pra acabar!!
Chama :
Voltando para :
Juntando tudo:
Juntando as constantes: