Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.8 - Ex. 1
Marque o ponto cujas coordenadas esféricas são dadas. A seguir, encontre as coordenadas retangulares do ponto.
(a)
(b)
Passo 1
E aí, turma! Beleza?
A questão quer que a gente marque, ou seja, localize um ponto em coordenadas esféricas e depois pede para encontrarmos o equivalente desse ponto em coordenadas retangulares:
As relações entre coordenadas esféricas e coordenadas retangulares são dadas da seguinte forma:
Então, vamos precisar usar as equações acima para transformar nosso ponto em um ponto de coordenadas retangulares. Depois que tivermos esse ponto em coordenadas retangulares, fica mais fácil localizar ele, já que já estamos acostumados a pensar nos eixos , e .
Vamos lá.
Passo 2
Show de bola, galera.... Pra resolver essa questão não tem mistério.
Basta nos lembrarmos do conceito de coordenadas esféricas para encontrarmos os pontos em coordenadas retangulares equivalentes.
Desta forma fica fácil, né? Os nossos pontos ficam da seguinte forma:
Para coordenadas retangulares, procuramos , ou seja:
Substituindo:
Substituindo pelos valores de cada variável pelo valor delas no ponto:
Fazendo esse cálculo:
Passo 3
Repetindo o mesmo processo para:
Substituindo:
Substituindo pelos valores de cada variável pelo valor delas no ponto:
Fazendo esse cálculo:
Passo 3
Como vimos no passo 1, é mais fácil localizarmos esses pontos usando seus valores em coordenadas retangulares. Esses pontos são localizados da seguinte forma:
(a) Como os valores de e são nulos, nosso ponto se encontra em cima do eixo :
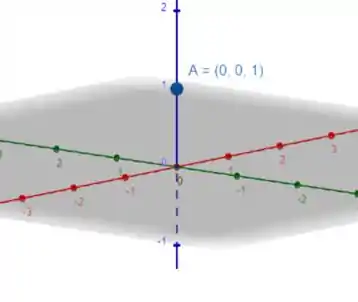
(b)
Plotando o ponto , temos:
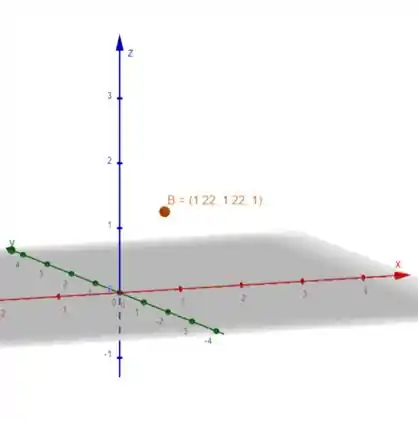
Resposta
(a)
(b)