Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 15
Um sólido está acima do cone e abaixo da esfera . Escreva uma descrição do sólido em termos de desigualdades envolvendo coordenadas esféricas.
Passo 1
Fala, galerinha! Tranquilidade?
Nossa questão quer que a gente descreva o sólido dado usando desigualdades de coordenadas esféricas. Esse sólido em questão é um cone com equação
Abaixo da esfera de equação
Quando falamos de coordenadas esféricas estamos falando de um sistema de 3 variáveis: e e funciona como esquematizado na imagem abaixo:
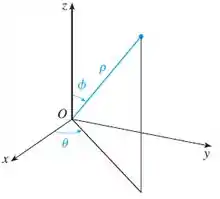
Esquema de representação de um ponto em coordenadas esféricas
A relação entre coordenadas retangulares e esféricas é dada por:
E também:
Então, o que precisamos fazer aqui é analisar nossa região e reescrevê-la usando essas variáveis, expressando em forma de desigualdade o intervalo que cada uma delas percorre.
Vem ver como fica!
Passo 2
Sabemos que o sólido satisfaz essa desigualdade
pois está acima do cone.
Elevando ao quadrado dos dois lados temos para eliminarmos essa raiz:
E aqui vai um truque sujo! Somando aos dois lados temos:
E olha só o que apareceu do lado direito! Das coordenadas esféricas, temos que:
Assim a desigualdade fica:
E como em coordenadas esféricas podemos substituir na desigualdade:
E tirando a raiz quadrada dos dois lados e racionalizando o lado direito vamos ter:
Ou seja! Como temos a parte de cima do cone, o ângulo vai variar de até !
Passo 3
Mas e Bom, ele deve satisfazer essa relação:
Pois o sólido está abaixo da esfera! Substituindo pela relação:
Temos:
Substituindo:
Ficamos com:
Simplificando:
Então, em coordenadas esféricas temos:
Por enquanto é isso pessoal, espero ter ajudado ;)