Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.6 - Ex. 2
Obtenha os gráficos de que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de e para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.
Passo 1
Fala meu querido!
Nessa questão temos a seguinte função:
E a partir dos gráficos de , e estimar os intervalos de crescimento, decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.
O gráfico da derivada , nos indica o crescimento da função de forma que:
Indica que a cresce e
Indica que a decresce.
indica que a função pode ter um valor extremo de forma que se a função crescia e depois decresce, esse ponto representa um máximo e se a função decrescia e depois cresce, esse ponto representa um mínimo.
O gráfico da segunda derivada , nos indica a concavidade da função de forma que:
Indica que a tem concavidade para cima e
Indica que a tem concavidade para baixo.
indica que a função possui um ponto de inflexão desde que nesse ponto a segunda derivada troque de sinal.
Para fazer essa questão vamos encontrar a derivada primeira e segunda dessa função e então plotar esses gráficos.
Para resolvermos este problema, é ideal que façamos primeiramente as derivações necessárias e encontremos os pontos de interseção com o eixo para em seguida, esboçarmos os gráficos, okay?
Passo 2
Nossa função é:
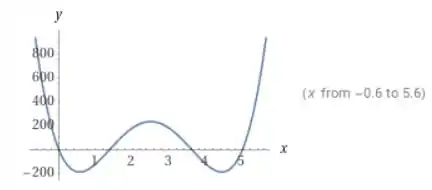
Seu gráfico é:
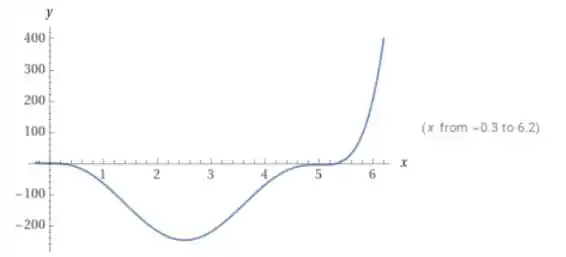
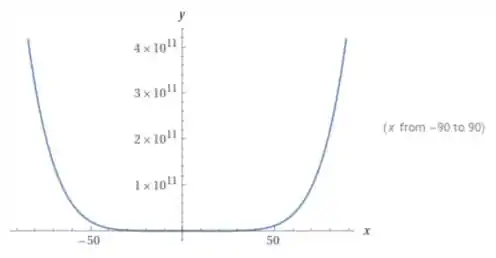
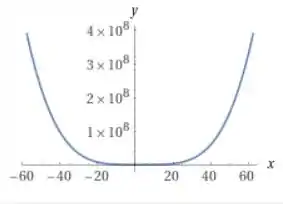
E com uma janela gráfica maior temos:
Fazendo a derivada primeira:
O gráfico da derivada é:
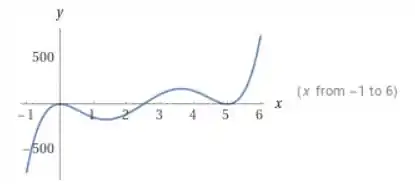
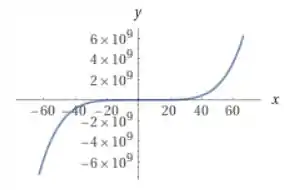
E com uma janela gráfica maior temos:
Por fim, a segunda derivada vale:
E o gráfico da segunda derivada é:
Com uma janela gráfica maior temos:
Passo 3
Fazendo as estimativas, temos que:
Para o gráfico , nós estimamos que e portanto é decrescente em temos que em ;
Portanto temos um mínimo local em .
Para o gráfico de , estimamos que e tem concavidade para cima em e e . E, e tem concavidade para baixo em e .
Os pontos de inflexão são localizados em , , e .
Finish!!
Resposta
Fazendo as estimativas, temos que:
Para o gráfico , nós estimamos que e portanto é decrescente em temos que em ;
Portanto temos um mínimo local em .
Para o gráfico de , estimamos que e tem concavidade para cima em e e . E, e tem concavidade para baixo em e .
Os pontos de inflexão são localizados em , , e .