em que a, b e c são parâmetros positivos, é conhecido como o sistema de Rössler. 20 É um sistema relativamente simples que consiste em duas equações lineares e uma terceira equação com uma única não linearidade quadrática. Nos problemas de 11 a 15, pedimos que você faça algumas investigações numéricas sobre esse sistema com o objetivo de explorar sua propriedade de duplicação de período. Para simplificar, faça , e deixe permanecer arbitrário.
11. (a) Mostre que não existem pontos críticos quando , existe um único ponto crítico quando e existem dois pontos críticos quando .
(b) Encontre o(s) ponto(s) crítico(s) e determine os autovalores correspondentes da matriz jacobiana quando e quando .
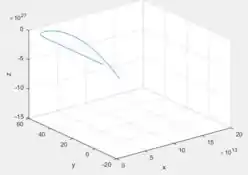
(c) Como você acha que será o comportamento das trajetórias do sistema para ? Desenhe a trajetória que começa na origem. Ela se comporta da maneira que você esperava?
(d) Escolha um ou dois outros pontos iniciais e desenhe as trajetórias correspondentes. Esses gráficos estão de acordo com suas expectativas?
Passo 1
A primeira coisa que devemos aqui é substituir as derivadas por , já que estamos buscando os valores dos pontos críticos:
Da segunda equação...
E da primeira equação, tiramos que...
Jogando esses dois últimos resultados na última equação...
Poxa! Uma equação do segundo grau:
Sabemos que ela só tem então solução real se for maior ou igual a :
Portanto...
Então se , implica no e, portanto não teremos ponto crítico nenhum. De fato com teremos um único valor para e, portanto, para e também, logo um único ponto crítico nesse caso.
Agora se , então teremos dois valores possíveis para , cada um gera um par de e , ou seja, teremos então dois pontos críticos!
Passo 2
PRIMEIRO PARA :
Sabemos que esse caso é o que nos gera um delta igual a :
Logo, o único valor real de será...
Então do passo anterior, podemos tirar as informações de e ...
O ponto crítico no caso será...
E quanto a matriz Jacobiana? De acordo com a nossa teoria podemos tirar essa informação da matriz:
Onde...
Calculando essas derivadas parciais então...
Logo, o valor do nosso Jacobiano será no nosso único ponto crítico no caso será...
Simplificando um pouquinho...
Para extrair as informações de autovalores dessa matriz, podemos usar o auxilio computacional, já que o problema nos permite tal acesso . Aqui, vou utilizar o WOLFRAMALPHA, afinal ele é uma plataforma muito simples e eficaz. Basta você escrever a nossa matriz lá na barrinha de fórmula do Site e dar um enter, ganhando:
Sacou? Então temos um autovalor nulo e outros dois imaginários!
Passo 3
PRIMEIRO PARA :
Refazendo as continhas agora para ...
Dessa vez obtivemos dois valores para , então é de se esperar dois valores diferentes para e ...
Os dois pontos críticos nesse caso então serão...
O jacobiano desse primeiro ponto será então...
Jogando no Wolfram para obter seus autovalores ganharemos...
MAS CALMA, meu Jovem! Temos um segundo ponto crítico e que certamente precisa ser avaliado também!
Calculando os seus autovalores por sua vez obteremos...
Passo 4
Bem, como no caso de , obtivemos dois pontos críticos diferentes, onde para um deles...
Tivemos autovalores imaginários com a parte real negativa e a outra parte real positiva, é de se esperar que pontos próximos deste ponto referenciado aí em cima sejam assintoticamente estáveis, enquanto para regiões mais próximas do outro ponto seja instável.
No caso da origem, por ela estar mais próximo de:
É esperado que ela entre em estabilidade assintótica!
De fato, usando o mesmo código que utilizamos no exercício 6, mas adaptando para este exercício dessa forma aqui:
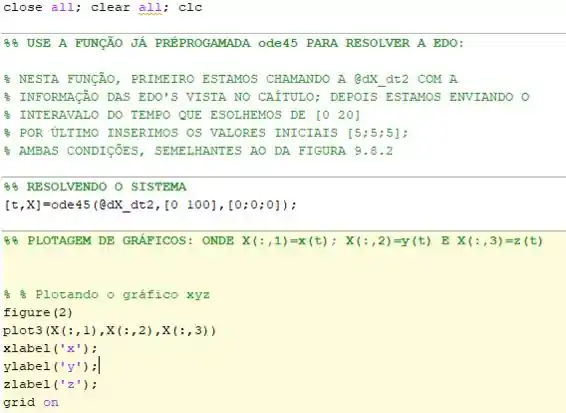
Onde a função de definição da EDO foi feita aqui separadamente:

Bem, mas plotando a solução para o ponto inicial de ...
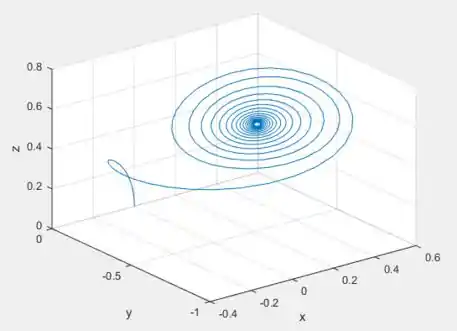
Viu só! De fato a nossa observação está certa! A solução tende a estabilidade ;)
Passo 5
Para um ponto inicial ...
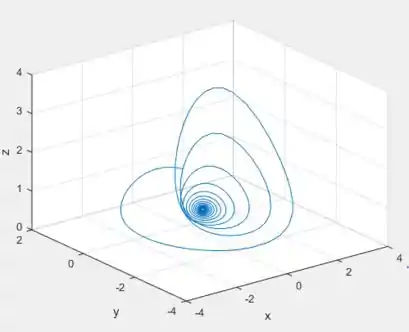
Temos a convergência.
Para um ponto ...
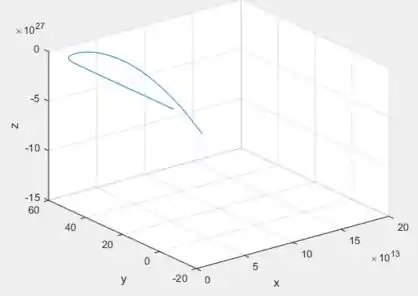
Temos uma divergência, bem como previmos!
Resposta
Letra A: Demonstração.
Letra B:
Letra C:
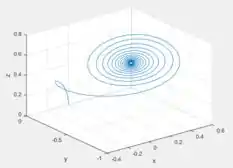
Letra D: Ponto :
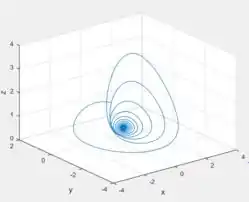
Ponto :