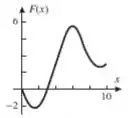
Seja , onde é a função do gráfico a seguir.
(a) Encontre , , , e .
(b) Em quais subintervalos de é crescente e em quais é decrescente?
(c) Onde toma seu valor máximo e onde toma seu valor mínimo?
(d) Esboce o gráfico de .
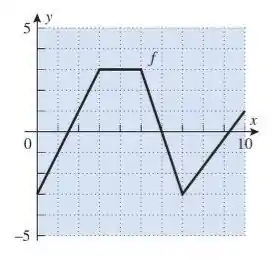
Passo 1
(a) Ok, para achar os valores de , precisamos apenas calcular os valores das áreas de nos intervalos da integral, já que é a área de em algum intervalo.
Para isso, vamos encontrar as retas que definem .
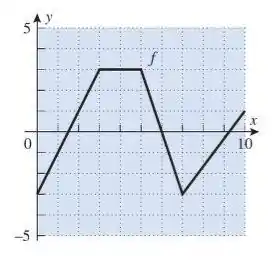
De até , é uma reta que passa pelos pontos e :
Então, de a :
De até , é uma reta que constante em .
De até , é uma reta que passa pelos pontos e :
e
Então, de a :
E de a , é uma reta que passa pelos pontos e :
e
Então, de a :
Então:
Passo 2
Para achar , vamos calcular:
Para achar , vamos calcular:
Para achar , vamos calcular:
Para achar , vamos calcular
Para achar , vamos calcular
Passo 3
(b) Para saber onde é crescente e decrescente, precisamos derivar essa função e ver onde a derivada é positiva e onde é negativa. Show! Então, vamos calcular a derivada disso aí:
Opa, então, o que vai mandar no sinal da derivada de é o próprio que achamos. Onde é positivo, é crescente, e onde é negativo, é decrescente.
Olhando para o gráfico de , vemos que:
é crescente em e
E
é decrescente em e
Passo 4
(c) Para saber os máximos e mínimos, temos que saber os pontos críticos, ou seja, onde . Temos, então:
E em , e .
Pela reposta do item anterior, vemos que decresce de até , depois cresce até . Ou seja, pode ser o nosso mínimo. Além dele, temos que decresce de até , depois cresce até . Ou seja, pode ser o nosso mínimo também. Só que se a gente calcula os valores de nesses pontos, vemos que:
E:
Com isso, é o ponto de mínimo e seu valor é .
E o único ponto que pode ser de máximo é em e seu valor é:
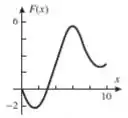
Passo 5
(d) Então, já temos os pontos de máximo e mínimo;
O intervalo que vamos esboçar a função;
Onde é crescente e decrescente.
Juntando todas essas informações e os valores em cada pono que discutimos anteriormente, chegamos nesse gráfico:
Resposta
(a) ; ; ; ; .
(b) é crescente em e e é decrescente em e .
(c) é o ponto de mínimo e seu valor é e é o ponto de máximo e seu valor é .
(d)