Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 4.5 - Ex. 37

Seja f x , y = x 2 + y 2 + 1 ,   s e   x 2 + y 2 < 1 0 ,   s e   x 2 + y 2 ≥ 1

a) Esboçar o gráfico de f .

b) Calcular, se existirem, ∂ f ∂ x ( 0 ,   1 ) , ∂ f ∂ y 1 ,   0 e ∂ f ∂ y ( 0 ,   0 ) .

Passo 1

Letra a)

Aplicando as funções em seus devidos intervalos em ferramentas gráficas obtemos o gráfico de f que se dá:

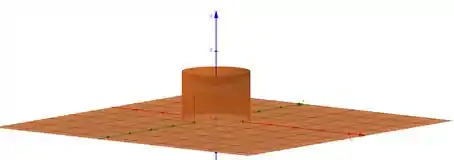
Passo 2

Letra b)

Primeiramente, devemos obter as derivadas parciais para x e y :

∂ f ∂ x = x x 2 + y 2 + 1

∂ f ∂ y = y x 2 + y 2 + 1

As derivadas parciais existem.

Agora, para finalizar, devemos aplicá-las os pontos dados:

∂ f ∂ x 0 ,   1 = 0 0 + 1 2 + 1 = 0

∂ f ∂ y 1 ,   0 = 0 1 2 + 0 + 1 = 0

∂ f ∂ y 0 ,   0 = 0 0 + 0 + 1 = 0

Resposta

a) Gráfico;

b) ∂ f ∂ x 0 ,   1 = 0 , ∂ f ∂ y 1 ,   0 = 0 e ∂ f ∂ y 0 ,   0 = 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as derivadas parciais de w x , y , z = x y z x + y + z
Calcule as derivadas parciais de f x , y , z = sin ⁡ x 2 + y 2 + z 2 .
Calcule as derivadas parciais de f x , y , z = x e x - y - z
Seja s = f x , y , z , w dada por s = e x y - z w . Verifique que x ∂ s ∂ x + y ∂ s ∂ y + z ∂ s ∂ z + w ∂ s ∂ w = 0
Calcule as derivadas parciais de w x , y , z = x 2 arcsin ⁡ y z