Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 2
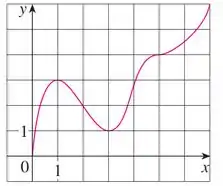
Usar o gráfico dado de f para encontrar o seguinte:
(a) Os intervalos abertos nos quais f é crescente.
(b) Os intervalos abertos nos quais f é decrescente.
(c) Os intervalos abertos nos quais f é côncava para cima.
(d) Os intervalos abertos nos quais f é côncava para baixo.
(e) As coordenadas dos pontos de inflexão.
Passo 1
- é crescente nos intervalos e .
- é decrescente no intervalo
- é côncava para cima (o “buraco” está voltado para cima, há um “formato de sorriso”) nos intervalos e .
- é côncava para baixo (o “buraco” está voltado para baixo, há um “formato de rosto triste”) no intervalo e .
- O ponto de inflexão é aquele onde a derivada troca de sinal, que no caso, são , e .
Passo 2
Passo 3
Passo 4
Passo
Resposta
- e .
- e .
- , e .
Exercícios de Livros Relacionados
Seja f t a temperatura no instante t onde você mora e suponha que no instante t = 3 você se sinta desconfortavelmente quente. Como você se sente em relação às informações dadas em cada caso?(a) f ' 3
Estime os intervalos da concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de f ' . f x = x 4 + x 3 + 1 x 2 + x + 1
Estime os intervalos da concavidade com precisão de uma casa decimal usando um sistema de computação algébrica para calcular e fazer o gráfico de f ' . f x = x 2 tg - 1 x 1 + x 3
(a) Use um gráfico de f para estimar aproximadamente os intervalos da concavidade e as coordenadas dos pontos de inflexão.(b) Use um gráfico de f ' ' para uma estimativa melhor. f x = x 3 x - 2 4
(a) Use um gráfico de f para estimar aproximadamente os intervalos da concavidade e as coordenadas dos pontos de inflexão.(b) Use um gráfico de f ' ' para uma estimativa melhor. f x = cos x + 1 2 co