Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 27

Use coordenadas polares para determinar o volume do sólido dado.

Dentro tanto do cilindro x 2 + y 2 = 4 e do elipsoide 4 x 2 + 4 y 2 + z 2 = 64 .

Passo 1

E aiiii turminha, tudo na paz? Partiu resolver!

Precisamos determinar o volume de um sólido em coordenadas polares. Sendo que esse solido, está limitado pelo cilindro x 2 + y 2 = 4 e o elipsoide 4 x 2 + 4 y 2 + z 2 = 64 .

Beleza, mas e agora! Como resolvo isso?

Vamos lembrar que o volume pode ser representado pela seguinte integral:

V = ∬ D z d A

Importante lembrar que temos duas regiões escritas em função de z , logo ao montar a integral ter cuidado de substituir o z pelo sólido elipsoide. Basta isolar o z .

Também precisamos definir os limites da região D para montar a integral iterada, que vai ficar com essa cara:

V = ∫ a b ∫ c d ( z ) d A

Nessa parte é importante fazer um esboço, para ajudar a interpretar.

Agora vamos escrever tudo em função de coordenadas polares:

x = r cos ⁡ θ ;                 y = r sen ⁡ θ

d A = r d r d θ

Sabemos que 0 ≤ θ ≤ 2 π , já para o intervalo do raio você vai ter que substituir a equação do cone dentro da equação da esfera tudo em coordenadas polares.

Agora, ficou tranquilo ein!! Vamos colocar mão na massa então!

Passo 2

Em coordenadas polares, temos que:

x = r cos ⁡ θ

y = r sen ⁡ θ

Sendo assim, quando nos é dada a condição de que:

x 2 + y 2 = 4

Sabemos que

x 2 + y 2 = r cos ⁡ θ 2 + r sen ⁡ θ 2 = r 2

Logo,

r 2 = 4

r = 2

Reescrevendo a equação do elipsoide, ou seja, isolando o z . Vamos ter:

z 2 = 64 - 4 x 2 + y 2

z 2 = 64 - 4 r 2

z = ± 64 - 4 r 2

z = ± 2 16 - r 2

Observe o gráfico para auxiliar.

Devido a simetria do elipsoide vamos ter duas regiões para integração, uma delas no eixo z positivo e outra no eixo z negativo.

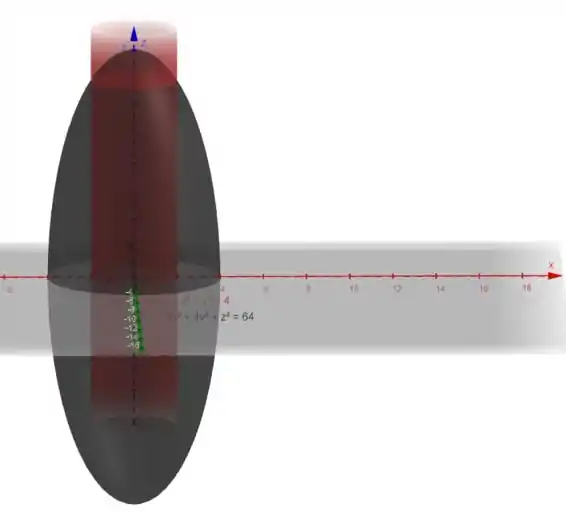
Por simetria, podemos dizer que:

z = 4 16 - r 2

Sabemos que o volume do sólido é dado por:

∬ D z d A

Onde D será a região delimitada por:

0 ≤ r ≤ 2 ,     0 ≤ θ ≤ 2 π

Passo 3

Agora é só montar nossa integral.

Como:

V = ∫ a b ∫ c d ( z ) d A

Onde:

d A = r d r d θ

0 ≤ r ≤ 2 ,     0 ≤ θ �� 2 π

E,

z = 4 16 - r 2

Vamos ficar com a seguinte integral,

V = ∫ 0 2 π ∫ 0 2 4 16 - r 2 r d r d θ

V = ∫ 0 2 π ∫ 0 2 4 r 16 - r 2 d r d θ

Resolvendo a integral de dentro, temos que aplicar a regra da substituição. Seja:

u = 16 - r 2

d u = - 2 r d r ∴   - d u 2 = r d r

Analisando os intervalos, temos que:

r = 0 → u = 16

r = 2 → u = 12

Substituindo, temos:

V = ∫ 0 2 π ∫ 16 12 4 u - d u 2 d θ

V = ∫ 0 2 π ∫ 16 12 - 2 u d u d θ

Integrando em du:

V = ∫ 0 2 π - 2 2 3 u 3 / 2 16 12 d θ

Aplicando o limite de integração:

V = ∫ 0 2 π - 4 3 12 3 / 2 - 16 3 / 2 d θ

Temos que:

V = ∫ 0 2 π 4 3 64 - 24 3 d θ

Passo 4

Agora, temos uma integral simples em d θ :

V = ∫ 0 2 π 4 3 64 - 24 3 d θ

Integrando, temos:

V = 4 3 64 - 24 3 θ 0 2 π

Aplicando os limites de integração:

V = 4 3 64 - 24 3 2 π

Portanto o volume vale:

V = 8 π 3 64 - 24 3

Resposta

V = 8 π 3 64 - 24 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando coordenadas polares, calcular:f) int_0^(sqrt(2)) int_y^(sqrt(4 - y^2)) x d x d y
Calcular ∬_R^() sqrt(x^2 + y^2) d x d y , sendo R a região delimitada por x^2 + y^2 = 1 e x^2 + y^2 = 9 .
Calcular ∬_R^() x d x d y , sendo R a região delimitada por x^2 + y^2 - 4 x = 0 .
Usando coordenadas polares, calcular:g) int_0^2 int_0^y x d x d y
Calcular ∬ R ( x 2 + y 2 ) d x d y , sendo R é dada por:a) Círculo centrado na origem de raio a .