Use o gráfico da função
Para dizer o valor de cada limite, se existir. Se não existir, explique por quê.
Passo 1
Olá, meu querido estudante. Vamos para essa resolução?
A gente tem aqui a função:
E dado o gráfico dessa função, iremos dizer se os limites nas letras a,b e c, existem ou não.
Esboçando o gráfico da função com o auxílio do GeoGebra, ficamos com
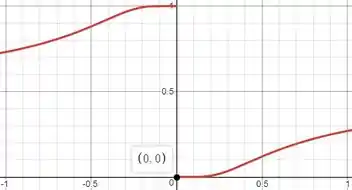
Para que calcularmos os limites laterais, devemos caminhar até o valor pela esquerda para valores e pela direita para valores mas sem chegarmos ao valor de fato, e sim infinitesimalmente menor que ele para e infinitesimalmente maior para .
Caso os valores dos limites laterais sejam iguais, nosso limite para existe, caso esses valores sejam diferentes, ele não existe.
Passo 2
Pelo gráfico, podemos ver que
- Ao nos deslocarmos pelo gráfico ao encontro de pela esquerda, estando infinitesimamente perto de porém para valores menores que , nossa função nos leva para , sendo assim:
- Ao nos deslocarmos pelo gráfico ao encontro de pela direita, estando infinitesimamente perto de porém para valores maiores que , nossa função nos leva para , sendo assim:
- não existe, pois os limites das letras (a) e (b) são diferentes
Resposta
- não existe, pois os limites das letras (a) e (b) são diferentes