Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.1 - Ex. 42
(a) Use o recurso de traçar gráficos implícitos de um CAS para esboçar o gráfico da curva cuja equação é .
(b) Use o gráfico de (a) para dar um palpite sobre a coordenada de um ponto do primeiro quadrante que está em e no qual a reta tangente a é paralela à reta.
(c) Use derivação implícita para verificar a conjectura em (b).
Passo 1
(a) Vamos usar aqui a calculadora CAS do Geogebra (dá para acessar pelo navegador) para esboçar esse gráfico aí.
Colocando a equação do enunciado lá, temos esse gráfico aqui:
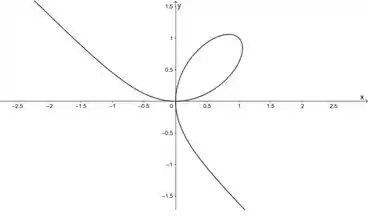
Passo 2
(b) Escolher um ponto onde a reta tangente é paralela à reta é o mesmo que escolher um ponto onde o gráfico da nossa função está a aproximadamente a no sentido horário.
A gente pode escolher esse ponto aqui:
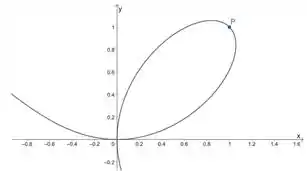
Onde:
Nossa estimativa é:
Passo 3
(c) Para verificar a nossa consejctura temos que ver se no ponto o coeficiente angular da nossa reta tangente é igual ao coeficiente de , que é . Isso demonstra que nesse ponto, elas são paralelas.
Já que:
Vamos ter que derivar a nossa equação implicitamente.
Vamos lá!
Passo 4
Derivando nossa equação dos dois lados:
Como é uma função de , em temos um produto de funções e em temos uma função composta, por isso a gente precisa usar a regra do produto e a regra da cadeia:
Agora isolamos para achar :
Passo 5
Vamos substituir o ponto para verificar se o nosso chute foi bom:
Deu igual ao coeficiente angular de , então nossa conjectura estava certinha. 😊
Resposta
- Conjectura estava certa. Verificação nos passos.