(a) Use seis retângulos para achar estimativas de cada tipo para a área sob o gráfico dado de de até .
(i) (pontos amostrais estão nas extremidades esquerdas)
(ii) (pontos amostrais estão nas extremidades direitas)
(iii) (pontos amostrais estão nos pontos médios)
(b) é uma subestimativa ou superestimativa em relação à área verdadeira?
(c) é uma subestimativa ou superestimativa em relação à área verdadeira?
(d) Entre os números , ou , qual fornece a melhor estimativa? Explique.
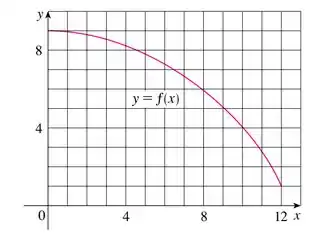
Passo 1
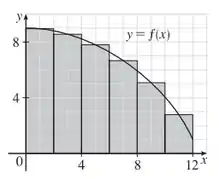
Nessa questão temos a seguinte curva
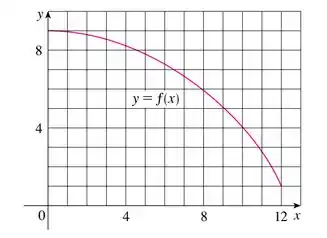
E vamos usar retângulos para encontrar sua área, bora lá?
Passo 2
(i) Primeiro encontraremos a estimativa superior com 6 retângulos, que podemos visualizar no seguinte gráfico:
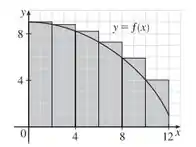
Nosso é:
Logo, é:
Passo 3
Encontraremos agora a estimativa inferior, que podemos visualizar no seguinte gráfico:
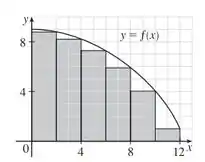
(Somamos o retângulo mais à direita, que não é utilizando em , e subtraímos o retângulo mais à esquerda, que é utilizando em mas não em ).
Passo 4
Fazendo a estimativa com os pontos médios temos o seguinte gráfico:
Passo 5
Como está decrescendo, nós obtemos uma superestimativa usando os pontos extremos esquerdos, que representa.
Passo 6
Como está decrescendo, nós obtemos uma subestimativa usando os pontos extremos direitos, que representa.
Passo 7
dá uma melhor estimativa, porque a área de cada retângulo aparenta ser mais próxima da verdadeira área que os retângulos subestimados e superestimados de e .
Resposta
(i)
(ii)
(iii)
Superestimativa
Subestimativa