Quando estudam a formação de cordilheiras, os geólogos estimam a quantidade de trabalho requerida para levantar uma montanha do nível do mar. Considere uma montanha que tem essencialmente o formato de um cone reto circular. Suponha que a densidade de peso do material na vizinhança de um ponto é e a altura é .
- Determine a integral que representa o trabalho total exercido para formar a montanha.
- Assuma que o monte Fuji no Japão tem o formato de um cone circular reto com raio de 62.000 pés, altura de 12.400 pés e densidade constante de 200 lb/pé3. Quanto trabalho teria sido exercido para formar o monte Fuji se a terra estivesse inicialmente no mar?
Passo 1
Oi, galera! Tudo bom?
A questão tem duas partes. A primeira quer a integral que representa o trabalho total exercido para formar a montanha. Para isso, precisamos primeiro entender como expressar esse trabalho para um volume muito pequeno e através da integral, que é uma soma de todos esses volumes pequenos, considerar o volume total da montanha.
Já a parte (b) pede o trabalho exercido para formar o monte Fuji se ele estivesse ao nível do mar.
Bem, então usaremos a integral que encontrarmos na parte (a) para calcular esse caso específico, usando coordenadas cilíndricas, que vão facilitar a descrição da região cônica. Achamos os limites de integração e poderemos finalmente calcular nossa integral tripla e achar esse trabalho.
Vem!
Passo 2
- Quando consideramos o trabalho para levantar um volume pequeno de material com densidade e altura , podemos escrever esse trabalho como:
- Vamos entender nossa região para termos os limites de integração. é uma região sólida de um cone circular reto, com raio , altura densidade lb/pé3. Podemos usar coordenadas cilíndricas para descrever nosso sólido:
Somando para a montanha inteira, temos:
Onde é a região cônica sólida que compreende a montanha.
Passo 3
- Podemos considerar o eixo do cone em , o cone varia de 0 até a altura total do sólido, então:
- A projeção de um cone circular no plano será uma circunferência de raio variável de acordo com a variação de , ou seja, na ponta do cone a circunferência é menor e vai aumentando conforme vamos em direção a base, por isso vamos expressas em função de .
- Como estamos tratando de circunferências, nosso ângulo terá variação de:
Passo 4
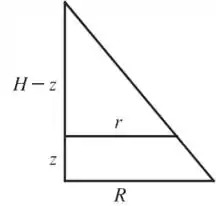
Meia seção transversal do cone
Temos por semelhança de triângulos:
Fazendo a subtração de frações, ficamos com:
Então podemos isolar :
Pronto, agora já sabemos que a variação do raio é:
Para coordenadas cilíndricas também temos:
Passo 5
Montando nossa integral, deixando a integral de “pra dentro” já que ela tem função nos limites de integração, ficamos com:
Substituindo as funções, sabemos que a densidade é constante e foi dada no enunciado. A altura podemos deixar em função de , então:
Vamos começar a integrar em , tratando como constante:
Aplicando os limites de integração:
tirando a constante para fora da integral e abrindo a fatoração dentro da integral:
Integrando em , tratando as outras variáveis como constantes
Realizando a integral em :
Ficamos com:
Integrando em :
Substituindo os limites:
Simplificando, temos afinal:
Passo 6
Agora é só usarmos a expressão que acabamos de encontrar substituindo para os nossos valores do Monte Fuji. Dos dados do enunciado:
lb-pé
Resposta
- lb-pé