Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 5
Você está planejando construir uma caixa retangular aberta com uma folha de papelão de , recortando quadrados congruentes dos vértices da folha e dobrando suas bordas para cima. Quais são as dimensões da caixa de maior volume que você pode fazer dessa maneira? Qual é o maior volume?
Passo 1
Vamos primeiro entender como é a situação. Ele pegou uma folha e cortou quadrados nas pontas. Se chamarmos de o lado desse quadrado, podemos ver na figura abaixo como fica representado esse corte:
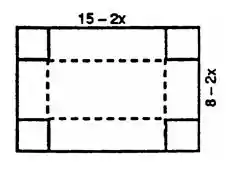
Peeeeera, mas o que é aquele e o ?
Repare que a caixa tem medida de , quando tiramos um quadrado de cada canto, vamos tirar de medida em cada canto também. Então, a nossa caixa tem medidas:
E seu volume vai ser o produto dessas medidas.
Passo 2
Vamos ter que a fórmula do volume vai ser
Abrindo essa conta, vamos ter:
Só um pequeno detalhe, aquele tem um intervalo que ele vale. Isso porque ele é uma medida, então precisa ser positiva.
Além disso, os dois lados da caixa precisam ser positivos, fazendo com que:
E
Assim, vamos ter
Assim, devemos ter:
Passo 3
Para achar o maior possível, temos que achar o ponto de máximo de .
Para isso, temos que ver se existe algum ponto de máximo ou mínimo no intervalo de e comparar com os valores extremos do intervalo de
Vamos começar achando a derivada:
Ela vai ser em:
Vamos começar dividindo todo mundo por
Aplicando Bhaskaras:
Teremos:
Ou
Apenas o segundo valor está no intervalo de que queremos, então vamos focar só nele como ponto crítico.
Passo 4
Achamos o nosso ponto crítico. Vamos usar o teste da segunda derivada para conferir se ele é máximo ou mínimo ou nada rs
Vamos ver o valor da segunda derivada em .
Como a derivada deu negativa, pelo teste da segunda derivada, é valor de máximo local.
Passo 5
Vamos comparar agora os valores de em , que são os extremos do intervalo e o máximo local. Vamos usar a fórmula antes de fazer a distribuitiva porque é mais fácil de fazer conta:
Então vamos ter que a área máxima é .
Vamos achar as dimensões do retângulo.
Fazendo