Função Quadrática
Teoria
Introdução
Aqui vamos ver as funções de segundo grau. Como o nome diz, são funções em que aparece o termo:
Mas, não é somente isso. Esse termo precisa ser aquele de maior grau na função, ou seja, são funções de segundo grau:
Mas não é:
Pois o termo de maior grau é o . Tudo bem? A partir disso, podemos representar uma forma geral para a função de segundo grau, como fizemos para a função afim:
Onde , e são números reais. Aqui temos um detalhe importante: aquele valor junto ao precisa ser diferente de , caso contrário o não ia aparecer e não teríamos uma função de segundo grau.
Domínio
O domínio da função é bem tranquilo de achar. Como ela é:
E não temos nenhuma restrição para nenhum valor de , assim o domínio vai ser qualquer valor real de , e vamos ter:
Não vamos nos preocupar por enquanto com a imagem da função de grau. Vamos ver agora como é o se gráfico e entender seus componentes.
Gráfico da função de 2º grau
A primeira coisa é saber como é o gráfico desse tipo de função. Esse gráfico vai ser uma parábola, e saber como é essa parábola no eixo cartesiano é que é o grande detalhe dessa parte de gráfico. Primeiramente, você sabe como é uma parábola em geral? Ela é algo parecido com um arco:
Essa é uma parábola qualquer, só para você ver como é o desenho dela, puxa aí na sua mente... Não lembra bastante uma antena parabólica (Claro que a antena é 3D, aqui estamos falando de coisas planas) ou a trajetória que uma bola basquete faz ao ser arremessada na sexta?
Para desenhar a parábola precisamos de duas coisas:
- Raízes da função de segundo grau
- Concavidade da função de segundo grau
A primeira coisa a fazer é sempre achar as raízes dessa função de grau. Para isso fazemos:
Isso nada mais é, neste caso, que a equação:
Ou seja, para a achar as raízes da função de segundo grau, basta calcular as raízes da equação de segundo grau correspondente! Conforme vimos no tipo de equações de segundo grau, as raízes serão dadas pela fórmula de Bhaskara!
Considerando:
Escrevemos a solução como sendo:
Dependendo do valor de , temos:
- Se , temos raízes reais iguais.
- Se , temos raízes complexas distintas.
- Se , temos raízes reais distintas.
Em termos gráficos, isso implica em:
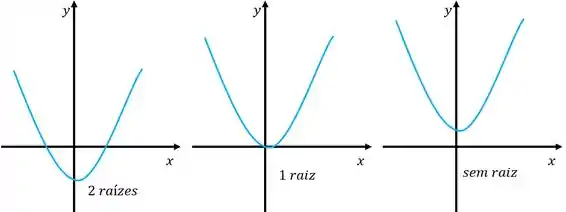
Ou seja, quando , temos a primeira situação, onde o gráfico cruza o eixo duas vezes. Para , temos a segunda, onde a parábola apenas tocará o eixo . Finalmente, quando , a função não tem raiz real e, portanto, nunca encontrará o eixo (triste).
Beleza, entendemos como achar as raízes e ver se são duas ou uma só e como isso afeta a posição da parábola. Agora temos que analisar a concavidade dessa parábola. Mas, você deve se perguntar: o que é essa tal de concavidade? Ela nada mais é para onde a parábola está virada - ou para cima ou para baixo. Os dois casos ficam assim:
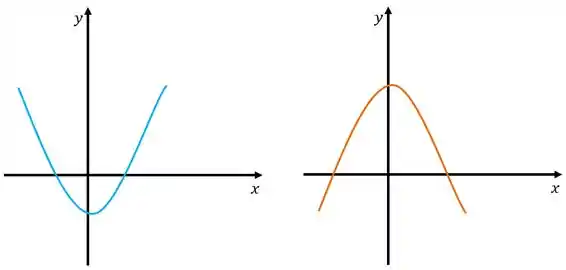
Nessa primeira em azul, a parábola está com a “barriguinha” virada para baixo, assim ela é côncava para cima. Enquanto a marrom (ou laranja dependendo do seu monitor) está com a “barriguinha” virada para cima, assim ela é côncava para baixo.
Outra forma de ver isso é fazendo uma setinha malandra na nossa parábola, vamos pegar o início da seta na parte que a parábola faz a curva, e depois apontar para o outro lado da parábola, ficando assim:
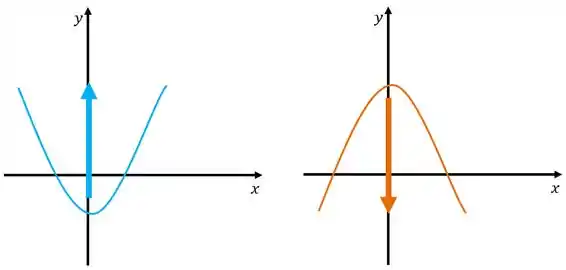
Assim, aquela que a seta aponta para cima é côncava para cima, a que a seta aponta para baixo é côncava para baixo.
Algebricamente, podemos saber essa concavidade pelo coeficiente da equação, que é aquele que multiplica o
- Se , o gráfico da função tem concavidade para cima;
- Se , o gráfico da função tem concavidade para baixo.
Vamos deixar aqui todas as situações possíveis de concavidade e quantidade de raízes só para você se familiarizar com isso de boa
Côncava para cima
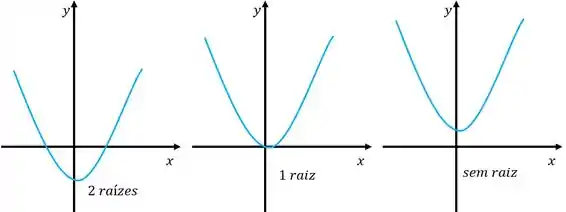
Todas essas três são côncavas para cima, o que muda aqui são as raízes.
Côncava para baixo
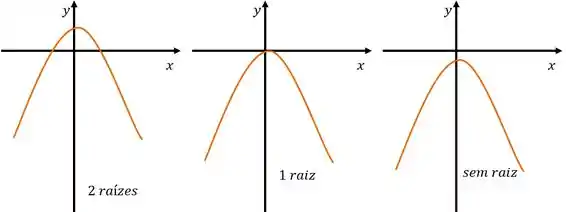
A ideia é exatamente a mesma para a outra concavidade. Agora que entendemos as duas partes principais, vamos um exemplo.
Determine o gráfico da
Vamos começar achando as raízes:
Podemos resolver por Bhaskara ou, neste caso, isolando o :
E temos as nossas duas raízes, que são diferentes. Além disso o valor de é , que é maior que , então ela é côncava para cima. O seu gráfico vai ficar
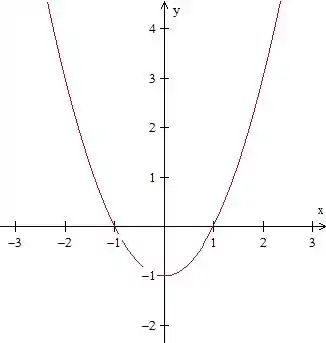
Vértice da parábola
Falta mais uma última coisa para ficar lindo. O último componente dessa parte de fazer o gráfico da função de grau é o seu extremo. Repara que a parábola, independente da concavidade, possui um ponto que faz a curva. Esse ponto é o extremo dessa parábola e também chamado de vértice. O valor do vértice é fácil de achar e determinado por:
Já o do vértice ou é determinado por:
Por exemplo, para temos:
Ou seja, o nosso vértice tem coordenadas
Para temos:
Vamos observar isso no gráfico?
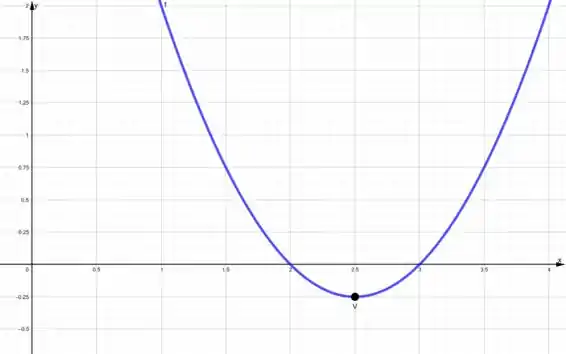
Imagem
A imagem da função de segundo grau está intimamente ligada ao seu vértice. Quando a função é côncava para cima, o seu vértice será o ponto de mínimo da parábola, e, portanto, a imagem será todos os valores iguais ou maiores que o ponto.
Já quando a função é côncava para baixo, o seu vértice será o ponto de máximo e a imagem, portanto, será todos os valores iguais ou menores que esse ponto.
No exemplo do , temos que:
Também, temos , ou seja, a função é côncava para cima e o valor do indica o ponto mínimo da função. Dessa forma, a imagem será:
#PartiuExercícios!!!
Gráfico da função de 2º grau
Vértice da parábola
Imagem
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Faça o esboço da seguinte função de grau
Passo 1
Essa questão é bem de boa né? Ele quer o esboço da função, para isso lembra quais as duas primeiras coisas a fazer? Essa é uma função de grau, então precisamos:
- Achar as raízes dessa função
- Achar a concavidade dessa função
Vamos começar com a raiz, que vai ser
Então
Assim vamos ter
Passo 2
Agora vamos para o segundo passo, que é achar a concavidade dessa função, repara que temos
Assim, como , essa função é côncava para baixo
Passo 3
Beleza, agora que sabemos essas duas informações podemos fazer o esboço do gráfico, mas antes de continuarmos vamos fazer umas contas a mais, só para deixar o nosso gráfico mais completo.
Vamos achar mais dois pontos, o extremo da parábola, e o ponto que ela corta o eixo .
O extremo, que é chamado de vértice vai ser
E
Agora vamos achar o ponto que ela corta o eixo , que vai ser quando
Assim
Passo 4
Vamos repassar as informações que achamos:
Agora é só fazer a nossa parábola
Eu marquei de diferentes cores os principais pontos que usamos só para você conseguir se localizar,
Resposta
Exercício Resolvido #2
Elaboração Própria
Ache as raízes de , obtenha e classifique como máximo ou mínimo o vértice e estude o sinal da função:
Passo 1
Beleza, vamos passo-a-passo. A raiz da função será quando:
Ou seja:
Agora é só fazer por Bháskara:
Assim:
Passo 2
Agora o jovem pediu para a gente classificar o vértice da parábola como máximo ou mínimo. Não pediu para calcular, só classificar como máximo ou mínimo. Para isso temos que ver a concavidade da função.
Como temos , e, portanto, a função é côncava para baixa.
Como é côncava para baixo, seu vértice será um ponto de máximo (sim, o contrário da concavidade).
Passo 3
Finalmente, temos que fazer o estudo do sinal da função, que é basicamente verificar quando é positiva ou negativa.
A função só muda de sinal quando passa pela raiz, então vamos verificar o sinal em cada intervalo formado pelas raízes.
Nesse caos, as raízes são:
Então, elas formarão intervalos:
Beleza, agora é só pegar algum valor dentro de cada intervalo (escolhemos sempre o mais conveniente) e esse valor terá o mesmo sinal que todo o intervalo, já que só muda de sinal quando passa pela raiz e os intervalos são limitados por elas. Para o primeiro filhote, podemos escolher:
Para o segundo, temos um valor bem bonito a nossa espera:
Para o terceiro:
Portanto, a função será positiva para:
E negativa para:
Onde esse significa união, ou junção desses intervalos.
Resposta
Raízes:
Vertíce é ponto de máximo.
Positiva para:
Negativa para:
Exercício Resolvido #3
AV1 Estácio de Sá
Complete as afirmativas (I), (II) e (III) abaixo. Da análise do discriminante da equação do 2º grau, podemos afirmar:
- Que se ______0, a equação terá duas raízes reais distintas.
- Que se ______0, a equação não terá raízes reais.
- Que se ______0, a equação terá uma única raiz real.
Passo 1
Escreva a equação de Bhaskara.
Analise o discriminante dentro da função raiz. Momentaneamente, esqueceremos o resto da equação, pois são números reais maiores que zero.
Passo 2
Agora escreva o domínio da função raiz, que contém o discriminate , sendo um numero real, temos:
,
Esse símbolo () lê-se “não existe”. No conjunto dos Reais, não existe raiz quadrada de um número negativo.
Resposta
- , duas raízes reais distintas
- , não existe raiz real.
- , apenas uma raiz real
Exercício Resolvido #4
UVA - Adriana Tostes - Lista 1 - 17
Uma bala é atirada de um canhão e descreve uma parábola de equação , onde é a distância e é altura atingida pela bala do canhão. Determine:
- A altura máxima atingida pela bala;
- O alcance do disparo.
Passo 1
Repare no gráfico. A altura máxima da parábola está localizada em seu vértice, que será:
Passo 2
Olhe novamente para o gráfico. A bola saí do chão , ou seja, saí da primeira raiz. Também atinge o chão em , na segunda raiz. Dessa maneira, alcance será:
Portanto, as raízes são:
Resposta
Exercício Resolvido #5
UVA - Fernando Marinho - Lista 1 - 5
Uma área retangular deve ser dividida ao meio, como indica a figura. Se você puder dispor de m de cerca, qual é a área máxima que consegue delimitar?
Passo 1
Vamos considerar a altura como e o comprimento como . Beleza. O perímetro será:
Pegando os três pedações verticais () e os dois horizontais () da figura.
Passo 2
A área do retângulo, por sua vez, será sempre base vezes altura, ou seja:
A partir da primeira equação, podemos substituir um dos valores. Isolando o :
Substituindo agora na equação da área:
Oh não! É uma parábola!!!!
Passo 3
Lembra que a gente está buscando área máxima que conseguimos delimitar? Então dentro da nossa função, a gente vai ter que buscar o máximo da parábola. E onde ela fica? No ponto de vértice:
Sabe o que aconteceu em ? Os Aliados invadiram a Normandia como parte da Operação (Dia D) para libertar a França dos Alemães. O que isso tem a ver com a questão? Nada!
Resposta
Exercício Resolvido #6
UVA - Adriana Tostes - Lista 1 – 22
Na figura temos os gráficos das funções e . Se , então calcule :
Passo 1
Aqui, temos dois pontos que sabemos que pertencem a reta da função . O primeiro é:
E:
Conforme o gráfico.
Passo 2
Com esses dois pontos, fica fácil determinar a reta , que terá o formato:
No segundo ponto:
Substituindo e colocando no primeiro ponto:
Portanto, a reta será simplesmente:
Passo 3
No ponto , teremos: