Série de Fourier apenas em senos ou cossenos
Produzido por Carolina SabaTeoria
Calcular todas aquelas integrais da série de Fourier é bem chato né? Vou te mostrar um macete que vai facilitar sua vida. Antes, deixa eu te mostrar uns detalhes técnicos aqui.
Lá na primeira teoria, eu te lembrei o que era uma função par e função ímpar. Agora, vamos ver como fica o produto entre funções?
- O produto entre duas funções pares é uma função par (pensa que (+)(+)=(+));
- O produto entre duas funções ímpares é uma função par (pensa que (-)(-)=(+));
- O produto entre uma função ímpar e uma par é ímpar (pensa que (+)(-)=(-))
E vou te contar mais um detalhezinho sobre as funções pares e ímpares. Se a função for par:
Se a função for ímpar, temos:
Fórmula de Euler- Fourier para funções pares e ímpares
Agora vamos aplicar essas ideias para as nossas fórmulas de Fourier (lembra que o seno é ímpar e o cosseno é par).
Lembrando que :
Onde é o período da nossa função
Funções pares
Se é par, então:
Logo, se é par, sua Série de Fourier apresenta apenas os ’s, sendo uma série de cossenos.
Onde
Ou seja, você não precisa calcular ! Pois ele sempre será zero.
Funções ímpares
Se é ímpar, então:
Logo, se é ímpar, sua Série de Fourier apresenta apenas os ’s, sendo uma série de senos.
Onde:
Ou seja, você não precisa calcular ! Pois ele sempre será zero.
Uma dica para decorar: como o cosseno é par, se é par ela será uma série de cossenos (logo ). Como o seno é ímpar, se é ímpar ela será uma série de senos (logo ).
Claro que sem se lembrar disso você ainda consegue resolver a questão, mas acaba fazendo contas desnecessárias e perdendo tempo! E o pior: você ainda pode errar alguma coisa no meio dessas contas! Então é uma boa gravar essas propriedades de funções pares e ímpares e saber reconhecer essas funções, ok?
Fórmula de Euler- Fourier para funções pares e ímpares
Exercícios Resolvidos
Exercício Resolvido #1
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 321. Exercício 15
Encontre a série de Fourier para a função dada e esboce o gráfico da função para a qual a série converge em um intervalo de três períodos.
Série em cossenos, período .
Passo 1
Vamos começar fazendo o gráfico, para a gente poder visualizar melhor a questão, ok? Primeiro, vamos desenhar os dados do enunciado:
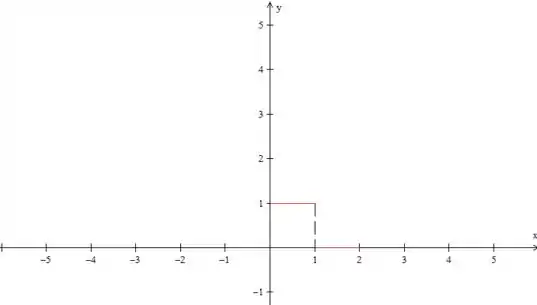
Até aqui nada demais, né? Como a questão pede uma série de cossenos, temos que fazer uma extensão par dessa função. Então, o próximo passo é espelhar isso que desenhamos do eixo , dessa forma:
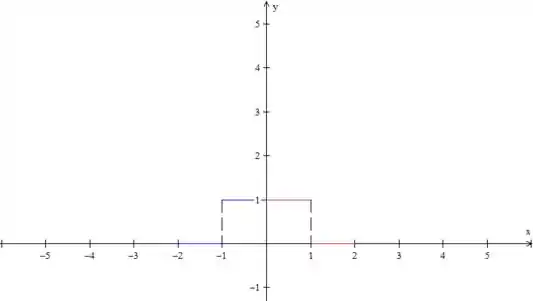
Bom, a função tem que ser periódica, né? Então vamos repetir esse padrão, para a esquerda e para a direita.
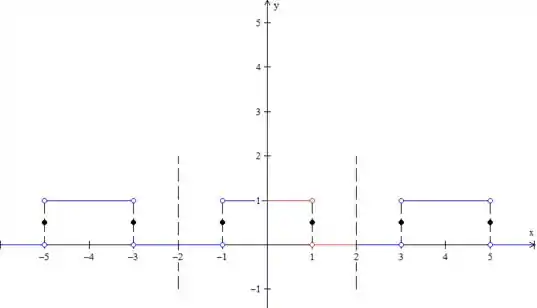
Pronto, temos então três períodos da função, como pede o enunciado. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de salto, a função vale a média dos limites laterais. Nesse caso:
Nós colocamos então as bolinhas cheias em (repare que todas as retas tem bolinhas vazias nas suas extremidades).
Passo 2
Beleza, agora temos que representar a função em série de Fourier. Como temos uma série de cossenos:
Como o problema pede (e podemos ver no gráfico), o período da função é . Logo
Assim
Passo 3
Agora vamos calcular
Fazendo na expressão de e , temos:
Agora temos que dividir essa integral em duas, pois vale em e vale em , temos então
Logo
Passo 4
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral em duas, como fizemos com :
Agora vamos analisar esse seno com calma.
Se é par, ou seja, se
Logo
Agora vamos analisar os ’s ímpares, fazendo , temos:
Logo, para ímpar, sendo
Então, podemos dizer que
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Vamos substituir agora o coeficiente . Repare que para , se anula, então só estamos interessados nos ’s ímpares, quando . Vamos então substituir isso na série.
Fazendo :
Para temos , portanto a série deve começar em .Temos então
Resposta
Exercício Resolvido #2
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 321. Exercício 16
Encontre a série de Fourier para a função dada e esboce o gráfico da função para a qual a série converge em um intervalo de três períodos.
Série de senos, período .
Passo 1
Vamos começar fazendo o gráfico, para a gente poder visualizar melhor a questão, ok? Primeiro, vamos desenhar os dados do enunciado:
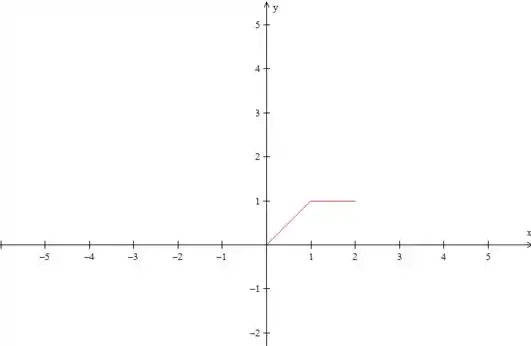
Até aqui nada demais, né? Como a questão pede uma série de senos, temos que fazer uma extensão ímpar dessa função. Então, o próximo passo é espelhar isso que desenhamos do eixo , dessa forma:
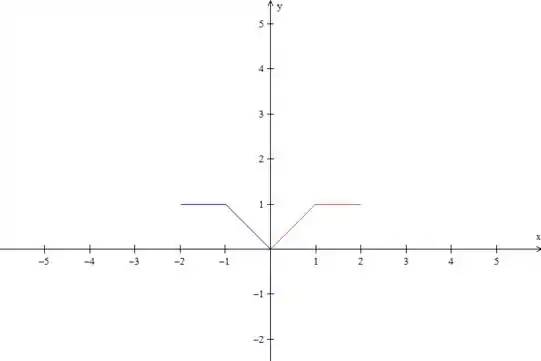
Mas isso seria uma extensão par, não é? Pra fazermos uma extensão ímpar temos que rebater essa parte azul no eixo , ou seja, jogar ela para baixo:
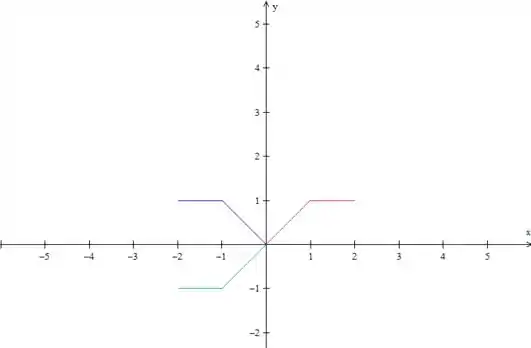
Certo, o período da função que queremos é então essa parte verde mais a vermelha! Como esse é o padrão que se repete, vamos copiá-lo, tanto para a esquerda como para a direita, olha só:
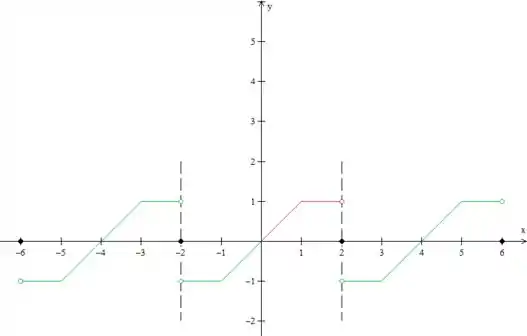
Pronto, temos então três períodos da função, como pede o enunciado. É bom você sempre desenhar esse tracejado grande para marcar o período da função, para não se perder!
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de salto, a função vale a média dos limites laterais. Nesse caso:
Nós colocamos então as bolinhas cheias em repare que todas as retas tem bolinhas vazias nas suas extremidades). Não poderia ser diferente, né? Uma extensão periódica ímpar sempre apresenta:
Como a gente já viu.
Passo 2
Beleza, agora vamos montar o problema. Como a função é ímpar, temos o seguinte:
Como o período da função é como o enunciado pediu, temos:
Passo 3
Vamos calcular os ’s. Temos que:
Como temos mais de uma expressão para em , precisamos dividir essa integral em duas:
Agora vamos fazer a integração por partes:
Como essa expressão é um pouco complexa (já que envolve seno e cosseno), não vamos fazer aquela análise para ’s pares e ímpares ok? Vamos deixar assim mesmo.
Passo 4
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Resposta
Exercício Resolvido #3
Séries de Fourier – funções pares e ímpares
Seja uma função de período tal que para todo .
- Sabendo que é uma função ímpar, determine a expressão de no intervalo .
- Determine a série de Fourier da função .
- Usando o item (b), calcule a soma da série numérica . Justifique sua resposta.
Passo 1
Letra a)
Vamos fazer um desenho dessa expansão de , ok?
Essa é a definição de que o problema deu de a :
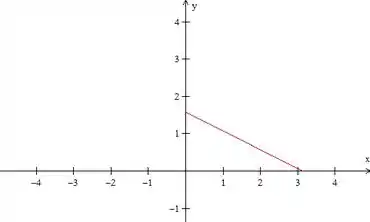
Vamos fazer a extensão ímpar dessa função, porque o problema pede uma série de senos. Primeiro nós espelhamos ela em relação ao eixo
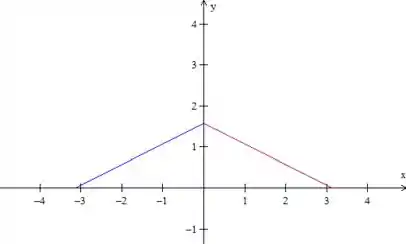
Espelhamos essa reta azul no eixo :
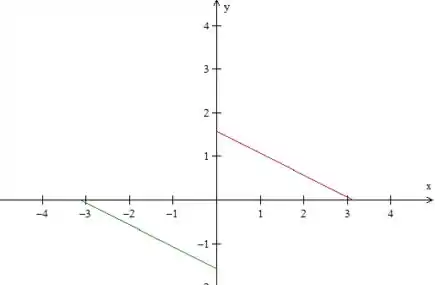
O período de é então essa parte verde mais a vermelha, para termos uma função em série de senos temos que ter ímpar como já vimos, para isso devemos pegar a função entre e , fazendo essa marotagem que fizemos ali de espelhar no eixo e depois no eixo , isso garante que nossa função seja ímpar, mas para isso tudo dar certo temos que pegar de à fazendo o período ser
Passo 2
Tá, mas o que o problema pede é a expressão de para . Nós sabemos que
para todo .
Como a função é ímpar, sabemos que
Logo, a expressão de para o intervalo que o problema quer é dada por:
Passo 3
Letra b)
Beleza, agora vamos montar o problema. Como a função é ímpar, temos o seguinte:
Como o período da função é , temos:
Passo 4
Vamos calcular os ’s. Temos que:
Agora vamos substituir a expressão de :
Agora vamos fazer a integração por partes:
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Passo 6
Letra c)
Como é seccinalmente contínua, temos que
Em todo ponto de continuidade de . E, como é contínua em , temos:
Resposta
Exercício Resolvido #4
UNICAMP - Cálculo 3 - Exame 2013 - 5
Seja a função ímpar, periódica de período e tal que se .
Encontre a série de Fourier de .
Mostre que
Passo 1
Para calcular a série de Fourier, primeiro identificamos o período . Portanto, .
Assim, a série é dada por:
Passo 2
Beleza, mas qual é a extensão ímpar da função?
É a seguinte:
Já dá pra ter uma ideia que é uma função dente de serra né... ok, vamos as contas agora!
Passo 3
Para calcular os coeficientes da Série de Fourier, lembremos que a função é ímpar. Ou seja, só sobram os termos em seno.
Como e são ímpares, seu produto é par. Assim,
Passo 4
Para o segundo termo, vamos usar integração por partes:
Substituindo:
Passo 5
Então, nós obtemos que
Passo 6
Para mostrar que
vamos fazer o seguinte: vamos tomar (você vai ver que os senos serão fáceis de calcular assim!).
Pela série de Fourier, temos:
Mas, da expressão de , sabemos que . Assim, podemos afirmar
Passo 7
Perfeito, agora vamos olhar pro somatório: se for ímpar, o seno dá ; se for par, o seno dá . Então vamos escrever :
Se for ímpar, o seno dá ; se for par, o seno dá . Pronto, isso é .
E, finalmente:
Agora, se você troca por (o que dá na mesma), obtemos a relação desejada!
Resposta
Exercício Resolvido #5
USP - Cálculo 4 - P2 2012 - 2b
Seja
a)Determine a série de Fourier de senos de
b)Mostre que a série de Fourier de senos de converge para uma função e esboce o gráfico da função em
c)Determine
Passo 1
a)Calma galera, você pode estar pensando, mas cara, essa função é par!!! Como fazer ela como uma série de Fourier de seno se essa série só existe pra função ímpar? Mas opa, ele só definiu a função de , se a gente definir em , pronto esse moleque é ímpar!
Bem bem, a série de Fourier de seno é:
]
:
A segunda integral vamos resolver de forma indeterminada primeiro, ela é maiorzinha:
Vamos fazer uma integração por partes:
Assim fica:
Agora para resolver essa outra integral, novamente outra integração por partes:
Então simbora:
Desenvolvendo:
Então vimos que:
Substituindo:
Mas:
Assim finalmente:
]
E com isso a série de Fourier de seno fica definida:
Passo 2
b)A extensão dessa função é seccionalmente contínua, e seccionalmente de classe , logo pelo teorema de convergência da série de Fourier, esta série converge a toda extensão em , exceto nos pontos de descontinuidade!
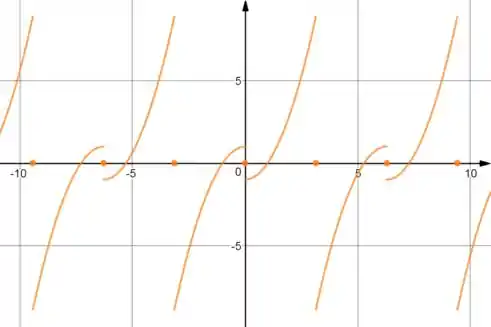
Então a função fica assim:
E é só repetir o período que não tem erro!
O gráfico ficou:
Passo 3
c)
Ae tu fica, “É clã, soldado morreu na trincheira” Mas calma, lembra que isso é uma função periódica e uma função ímpar, a cada 1 período a área necessariamente tem que dar zero!, vamos reescrever isso:
Para facilitar mais ainda, podemos tirar mais coisa:
Mas opa, a gente viu que dentro de a função que rege isso é:
Logo:
Resposta
a)
b) A extensão dessa função é seccionalmente contínua, e seccionalmente de classe , logo pelo teorema de convergência da série de Fourier, esta série converge a toda extensão em , exceto nos pontos de descontinuidade
c)
Exercício Resolvido #6
USP - Cálculo 4 - P2 2011 - 2b
Determine , de modo que
Seja mínimo.
Passo 1
b)
Galera, pensa comigo, pra minimizar aquela integral que ele quer, basta minimizar o cara ao quadrado
Repara que o período da integral é de a , isso nos dá uma ideia de que queremos uma extensão da função na verdade, isso porque ela só está definida naquele intervalo que ele deu.
𝐴 gente pode pensar no seguinte, a gente usa série de Fourier para aproximar funções, certo?
E se fizemos essa função que esta subtraindo de tender a ela mesma, opa, então esse cara vai tender a ser cada vez menor, estamos minimizando!
Então vamos calcular os coeficientes da série de Fourier da extensão de e eles serão e !
O primeiro detalhe é, mas qual a extensão que vamos tomar, a par ou a ímpar? Como queremos que apareça só seno ali vamos pegar a extensão ímpar daquela função.
Mas cuidado, estamos fazendo isso porque o termo que tá dentro da integral está a cara da série de Fourier, mas perceba que são os termos do somatório em e .
Assim
Sempre que ele pedir para minimizar essa parada é só fazer desse jeito.
Passo 2
A primeira coisa a fazer é a extensão ímpar daquela função, vamos chamar essa extensão ímpar.
Nesse caso só queremos os coeficientes da série de Fourier, então não vamos nos preocupar em achar o gráfico dessa extensão nem nada. Lembrando que quando pegamos uma extensão ímpar de vamos ter
E
A grande questão é, qual o limite dessa parada? Repara que eu falei de uma extensão ímpar daquela função que está no intervalo de à , então o nosso período vai ser , isso nos diz que
E
Então
Passo 3
Vamos agora achar e , começando com
Podemos escrever essa integral assim
Lembrando que
Vamos ter
Passo 4
Vamos agora achar
Podemos escrever essa integral assim
Lembrando que
Vamos ter
Passo 5
Então vamos ter
Resposta
Exercício Resolvido #7
UFRJ - Cálculo 4 - P2 2015.1 – 2a
- Determine a série de Fourier em cossenos da função:
Passo 1
Letra a)
Vamos começar fazendo o gráfico dessa função. Como o problema pede uma série de cossenos, sabemos que queremos uma extensão par de , certo?
Então, desenhamos em (em vermelho), espelhamos esse desenho em relação a (em azul) e repetimos esse período (em verde):
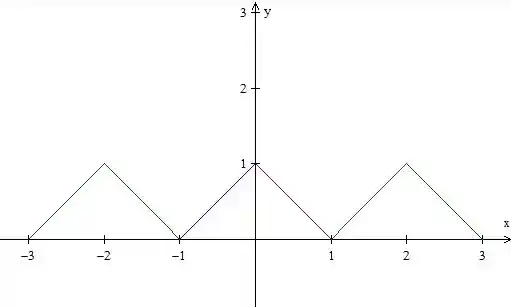
Passo 2
Beleza, agora vamos montar o problema. Como a função é par, temos o seguinte:
Como o período dessa função é , temos ,esse é intervalo em que ela se repete. Lembra que a função representada por Série de Fourier tem que ser periódica? Então
Passo 3
Agora vamos calcular
Fazendo na expressão de e , temos:
Como em , temos:
Logo
Passo 4
Agora vamos calcular os outros ’s. Temos que:
O que nos dá
Agora vamos fazer a integração por partes:
Como
Podemos escrever então
Guarde isso!
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
O que nos dá
Deixamos o por último que é mais chatinho.
Não podemos escrever direto no somatório porque isso só vale para ímpar! Vamos definir então , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em . Temos então
Você pode poderia ter definido , porém, nesse caso, o somatório iria começar em .