Considere um servomecanismo baseado num motor CC controlado pela armadura com função de transferência:
Projete um compensador de avanço de modo que o fator de amortecimento permaneça constante (), porém com tempo de acomodação para tolerância de de .
Passo 1
Precisamos determinar , e da função de transferência do compensador que satisfaça os critérios do enunciado.
O primeiro passo é definir o polo dominante, e para isso precisamos de e . O valor de já foi dado no enuciado e podemos calcular como abaixo:
O polo dominante pode ser encontrado pela fórmula:
Portanto:
Passo 2
Vamos representar os polos da função de transferência em malha aberta e os polos dominantes no diagrama de lugar das raízes
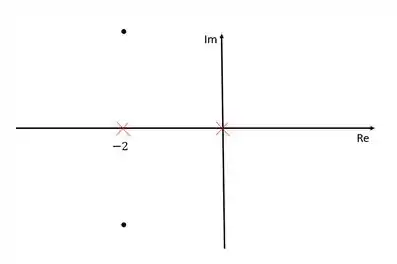
Os dois polos da função de transferência estão representados com um “xis” vermelho e os polos dominantes estão representados pelos pontos. Agora precisamos determinar o polo e o zero do compensador que faça com que o os polos dominantes façam parte do local das raízes. Existem infinitas combinações para esse polo e zero. Sendo assim, vamos arbitrar um valor para o zero e calcular o polo depois a partir desse valor de arbitrado do zero.
Uma tática é colocar o zero sobre o eixo dos reais com o mesmo valor do polo dominante. Nesse caso, o zero do compensador coincidiria com o polo da função de transferência que já existe em . Sendo assim, vamos arbitrar o zero um pouco para a esquerda, em .
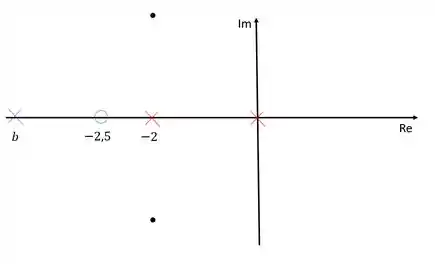
Passo 3
Devemos agora determinar o valor de . Para isso vamos ligar todos os polos e zeros ao polo dominante e calcular o ângulo formado:
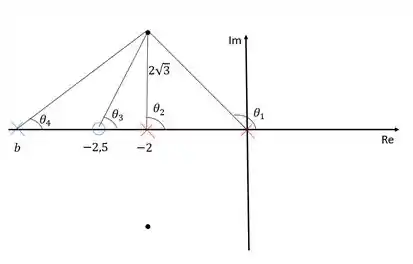
Para conseguir o ângulo , precisamos calcular os ângulos , e . Podemos calcular esses três ângulos utilizando o arcotangentes deles. Então vamos lá:
O ângulo é visto que está na mesma linha horizontal que o polo dominante.
A soma de todos os ângulos dos zeros e polos deve ser um múltiplo ímpar de , então:
Lembrando que os polos contribuem com ângulos negativos e os zeros comângulos positivos, então:
Sabendo o ângulo é possível calcular a localização do polo:
Como é a distância do polo até , o polo se encontrará em .
Passo 4
Por enquanto a função de transferência do compensador está assim:
Só resta então calcular o valor do ganho .
Para calular o ganho, devemos satisfazer a segunte condição:
O módulo dos polos e zeros pode ser obtido calculando-se a distância entre eles e os polo dominante:
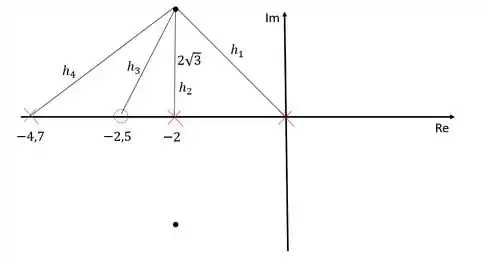
Dessa forma:
Portanto: