Uma partícula deslocando-se em uma dimensão (o eixo ) é descrita pela função de onda
Onde , , e o sentido positivo do eixo aponta para a direita.
- Determine de modo que a função de onda seja normalizada.
- Faça o gráfico da função de onda.
- Calcule a probabilidade de se encontrar essa partícula em cada uma das seguintes regiões.
- Até da origem
- Do lado esquerdo da origem (você pode adivinhar a resposta olhando para o gráfico da função de onda?).
- Entre e .
Passo 1
a) Determine de modo que a função de onda seja normalizada.
Para que a função de onda seja normalizada, ela deve obedecer à condição de normalização, dada por:
Passo 2
Onde:
;
Logo:
Passo 3
b) Faça o gráfico da função de onda.
A função de onda vai ser algo do tipo:
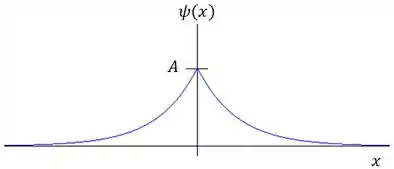
Passo 4
c) Calcule a probabilidade de se encontrar essa partícula em cada uma das seguintes regiões.
A probabilidade de se encontrar um elétron entre os pontos e , por sua vez, é dada por:
Passo 5
- Até da origem:
Como o problema fala de da origem, vamos calcular a probabilidade de se encontrar uma partícula entre e .
Para , e para , . Logo:
Onde:
;
;
Logo:
Passo 6
Do lado esquerdo da origem (você pode adivinhar a resposta olhando para o gráfico da função de onda?):
Do lado esquerdo da origem representa todos os valores negativos de e, de acordo com o gráfico, exatamente a metade do gráfico da função de onda .
Logo, a probabilidade de se encontrar uma partícula nessa região é .
Passo 7
Caso não dê pra identificar isso visualmente, podemos calcular a probabilidade com variando de até .
Para , . Logo:
Onde:
;
;
Logo:
Passo 8
Entre e .
Como estamos calculando a probabilidade em um intervalo onde , . Logo:
Onde:
;
;
Logo:
Resposta
a)
b)
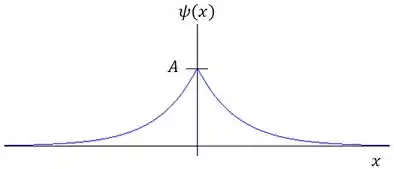
c)
(i):
(ii):
(iii):