Exercícios de Parâmetros Adimensionais - Lista de Exercícios Resolvida

Resultados experimentais para a transferência de calor sobre uma placa plana com superfície extremamente rugosa puderam ser correlacionados por uma expressão com a forma

Onde é o valor local do número de Nusselt na posição , medida a partir da aresta frontal da placa.

Obtenha uma expressão para a razão entre os coeficientes de transferência de calor médio e local .

(Adaptada) Foram efetuados experimentos para determinar coeficientes de transferência de calor locais para o escoamento perpendicular a uma longa barra isotérmica de seção transversal retangular. A barra tem largura , paralela ao escoamento, e altura , normal ao escoamento.

Para números de Reynolds na faixa de , os números de Nusselt médios nas superfícies são correlacionados por uma expressão na forma

Os valores de e para a face frontal, faces laterais e face posterior da barra retangular foram determinados e são mostrados a seguir:

Determine o valor do coeficiente de transferência de calor de cada face da superfície exposta em um barra retangular com e .

A barra está exposta ao escoamento cruzado de ar com e .

Ar forçado a e é usado para resfriar elementos eletrônicos em uma placa de circuito. Um desses elementos é um chip, que mede por , localizado a da aresta frontal da placa.

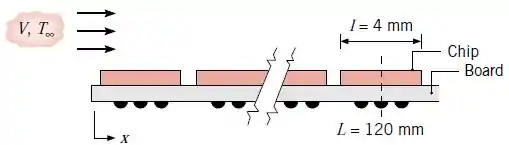
Experimentos revelaram que o escoamento sobre a placa é perturbado pelos elementos e que a transferência de calor por convecção é relacionada por uma expressão com a forma

Estime a temperatura superficial do chip se ele estiver dissipando .

O desembaçador de pára-brisa de carros funciona jogando ar quente na superfície interna do pára-brisa. Para evitar a condensação de vapor d’água nesta superfície, a temperatura do ar e o coeficiente convectivo na superfície devem ser grandes o suficiente para manter uma temperatura na superfície , que seja, pelo menos, superior ao ponto de orvalho .

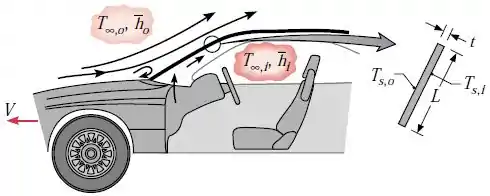
Considere um pára-brisa com comprimento e espessura , e condições de direção nas quais o carro se desloca a uma velocidade em um ambiente a .

Com base em experimentos de laboratório efetuados em um modelo do carro, sabe-se que o coeficiente de convecção médio na superfície externa do pára-brisa é correlacionado por uma expressão com a forma

, onde .

As propriedades do ar ambiente podem ser aproximadas por , e . Se e , qual é o menor valor de requerido para evitar a condensação na superfície interna?

(Adaptada) Considere o escoamento de ar sobre uma placa plana com comprimento , sob condições nas quais a transição ocorre em baseada em um número de Reynolds críticos de .

Calculando as propriedades termofísicas do ar a , determine a velocidade do ar.

Nas regiões laminar e turbulenta, os coeficientes convectivos locais são, respectivamente,

Onde, em , , e possui unidade de .

Desenvolva uma expressão para o coeficiente convectivo médio, , como uma função da distância da aresta frontal, , para a região laminar, .

Desenvolva uma expressão para o coeficiente convectivo médio, , como uma função da distância da aresta frontal, , para a região turbulenta, .