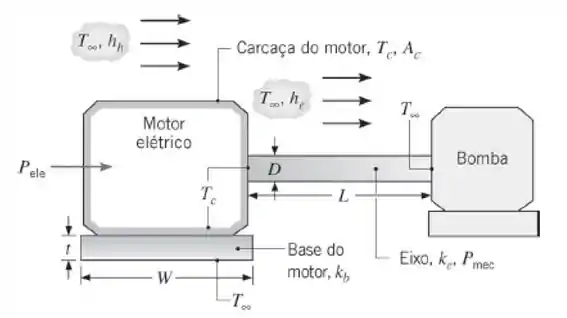
Um motor recebe potência elétrica de uma linha de força e transmite potência mecânica para uma bomba através de um eixo rotativo de cobre com condutividade térmica , comprimento L e diâmetro D. O motor está montado sobre uma base quadrada com lado de comprimento W, espessura t e condutividade térmica . A superfície da carcaça do motor,

exposta ao ar ambiente a , possui uma área e o coeficiente convectivo correspondente é . As extremidades opostas do eixo estão a temperaturas de e , e a transferência de calor do eixo para o ar ambiente é caracterizada por um coeficiente convectivo . A superfície inferior da base do motor está a .

1. Expressando o seu resultado em termos de , , , L, D, W, t, ,, e , obtenha uma expressão para ( – ).
2. Qual o valor de se ,

Animados para seguir?

Então boora lá !!

Sabemos que a potência elétrica está gerando potência mecânica e liberando calor. Este calor será transmitido para o ar por convecção, para a base do motor por condução, e por fim para a aleta,

Quando nós fazemos o balanço de energia teremos:

Agora nós precisamos achar cada um dos termos, ok?

A primeira coisa que devemos fazer aqui é escrever a equação de Fourier para a condução que ocorre a uma distância x:

Para a base:

A transferência de calor por convecção pode ser dada como:

E a última que precisamos achar é a transferência de calor para aleta, que neste caso será:

Quando o comprimento é L a temperatura é , então:

Por isso:

Os valores de M e m nós já conhecemos, certo?

Colocando tudo isso no balanço:

Isolando

E é isso galerinha, achamos nossa letra (a)!!

Mas ainda precisamos da letra (b), certo?