Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 49

Seja uma aleta unidimensional, com área de seção transversal uniforme, isolada na sua extremidade, x = L . A temperatura na base da aleta T b e a do fluido vizinho T ∞ , bem como o coeficiente de transferência de calor h e a condutividade térmica k , são conhecidas.

(a) Deduza a equação de diferenças finitas para qualquer nó interior m .

(b) Deduza a equação de diferenças finitas para um nó n localizado na extremidade isolada.

Passo 1

Vamos começar desenhando as duas situações, começando com o nó interior m :

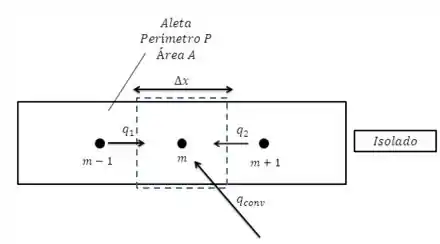
O balanço de energia em regime estacionário para o item (a) fica:

E ˙ e n t - E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q 2 + q c o n v = 0

Para o item (b) nosso volume de controle é:

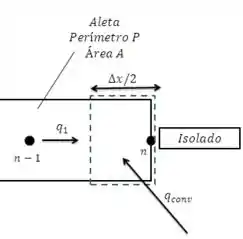
Para o item (b) o balanço de energia fica:

E ˙ e n t - E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q c o n v = 0

Vamos agora descrever cada taxa de transferência de calor para os dois itens separadamente.

Passo 2

Para o item (a):

q 1 = q m - 1 → m

q 1 = k A 1 L 1 ∆ T 1

q 1 = k A ∆ x T m - 1 - T m

q 2 = q m + 1 → m

q 2 = k A 2 L 2 ∆ T 2

q 2 = k A ∆ x T m + 1 - T m

q c o n v = h A c o n v ∆ T c o n v

q c o n v = h P ∆ x T ∞ - T m

Substituindo no balanço de energia:

k A ∆ x T m - 1 - T m + k A ∆ x T m + 1 - T m + h P ∆ x T ∞ - T m = 0

T m - 1 - T m + T m + 1 - T m + h P ∆ x 2 k A T ∞ - T m = 0

T m - 1 + T m + 1 + h P ∆ x 2 k A T ∞ - 2 + h P ∆ x 2 k A T m = 0

Passo 3

Agora para a situação de um ponto n localizado na extremidade isolada:

q 1 = q n - 1 → n

q 1 = k A 1 L 1 ∆ T 1

q 1 = k A ∆ x T n - 1 - T n

q c o n v = h A c o n v ∆ T c o n v

q c o n v = h P ∆ x 2 T ∞ - T n

Aplicando no balanço de energia do item (b):

k A ∆ x T n - 1 - T n + h P ∆ x 2 T ∞ - T n = 0

T n - 1 - T n + h P ∆ x 2 2 k A T ∞ - T n = 0

T n - 1 + h P ∆ x 2 2 k A T ∞ - 1 + h P ∆ x 2 2 k A T n = 0

Resposta

(a) T m - 1 + T m + 1 + h P ∆ x 2 k A T ∞ - 2 + h P ∆ x 2 k A T m = 0 .

(b) T n - 1 + h P ∆ x 2 2 k A T ∞ - 1 + h P ∆ x 2 2 k A T n = 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco circular delgado está sujeito ao aquecimento por indução a partir de uma bobina, cujo efeito é o de propiciar uma geração uniforme de calor no interior de uma seção anular, conforme mostrado
Um cabo elétrico, que experimenta uma geração volumétrica de calor a uma taxa uniforme q , encontra-se semienterrado em um material isolante, enquanto a sua superfície superior está exposta a um proce
Um bastão de tantálio, com 3m m de diâmetro e comprimento de 120m m , é sustentado por dois eletrodos no interior de um grande recipiente onde há vácuo. Inicialmente, o bastão está em equilíbrio com o
Placas de circuito impresso são empilhadas e tratadas pelo aquecimento sob alta pressão, como ilustrado no Problema 5.45 e descrito posteriormente no Problema 5.46. Busca-se uma solução pelo método de
Um bastão de sustentação ( k = 15W / ( m · K ) , α = 4,0 × 10 - 6m 2 / s ), com diâmetro D = 15m m e comprimento L = 100m m , atravessa um canal cujas paredes são mantidas a uma temperatura de T b = 3