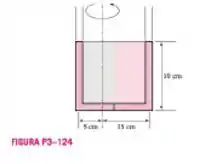
Um tubo em U contém água no braço direito e outro líquido no braço esquerdo. Observa-se que, quando o tubo em U gira a em torno do eixo que está a do braço direito e do braço esquerdo, os níveis de líquido em ambos os braços se igualam. Determine a densidade do fluido no braço esquerdo.

Começamos estabelecendo que a diferença de pressão entre dois pontos 1 e 2 é:

Calculando a velocidade angular, temos:

Tendo o seguinte diagrama:

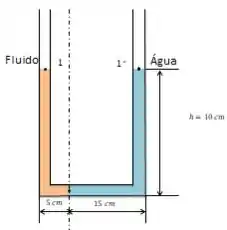
Concluimos que a pressão no ponto é igual para os dois fluidos, da mesma forma que as pressões nos pontos e , portanto, é o mesmo.

A diferença entre e nos dá , assim, para a água temos:

E, para o fluido que não conhecemos:

Igualando as duas expressões, temos:

Assim, substituindo os dados:

Prontinho!!