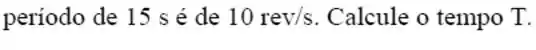Exercícios de Movimento Circular Acelerado - Lista de Exercícios Resolvida
Questão 1
O gráfico a seguir representa a velocidade angular, em função do tempo, de uma polia que gira ao redor de um eixo.
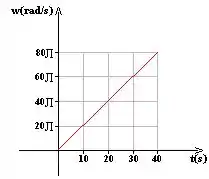
Com base nas informações contidas no gráfico, determine a aceleração angular desta polia e a quantidade de volta que ela dá no intervalo de tempo entre 0 e 40s.
Ver solução completaQuestão 2
A posição angular de um ponto da borda de uma roda que gira em torno de seu centro é dada por , onde está em radianos e em segundos.
Quantas voltas tal ponto dá em torno do centro da trajetória circular entre os instantes e ?
Questão 3
A aceleração de um corpo faz um ângulo de com a tangente do movimento, como mostrado na figura abaixo. Determine a equação que relaciona a velocidade angular e a aceleração angular.
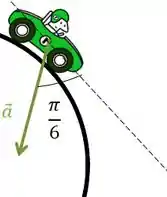
Questão 4
Um DJ, ao preparar seu equipamento, esquece uma caixa de fósforos sobre o disco de vinil, em um toca-discos desligado. A caixa se encontra a 10 cm do centro do disco. Quando o toca-discos é ligado, no instante t = 0, ele passa a girar com aceleração angular constante α = 1,1 rad/, até que o disco atinja a frequência final f = 33 rpm que permanece constante. O coeficiente de atrito estático entre a caixa de fósforos e o disco é μe = 0,09. Determine:a) a velocidade angular final do disco, , em rad/sb) o instante em que o disco atinge a velocidade angular c) a velocidade angular do disco no instante em que a caixa de fósforos passa a se deslocar em relação ao mesmoNote e adote:Aceleração da gravidade local g =10 m/s2.π = 3
Ver solução completaQuestão 5
A figura mostra dois discos que podem girar em torno de seus centros independentemente. No instante , as retas de referência dos dois discos têm a mesma orientação (como mostrado no desenho); o disco já está girando com uma velocidade angular constante e o disco parte do repouso com uma aceleração angular constante de.
a) Em que instante as duas retas de referência têm o mesmo deslocamento angular ?
b) Qual será o primeiro instante , após , para o qual as duas retas de referência estão paralelas com a linha que une o centro dos dois discos?
c) Considere agora que o deslocamento angular do disco varia no tempo com , onde está em radianos. Em qual instante a velocidade angular de é igual à velocidade angular de ?
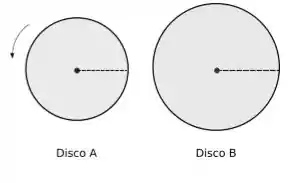
Questão 6
A roda-gigante da figura abaixo, gira no sentido contrário ao dos ponteiros de um relógio. Em dado instante, um passageiro na periferia da roda e passando no ponto mais baixo do movimento circular se move a e está ganhando velocidade com uma taxa de . a) Determine o módulo, a direção e o sentido da aceleração do passageiro nesse instante. b) Faça um desenho do passageiro e da roda-gigante mostrando o vetor velocidade e o vetor aceleração.
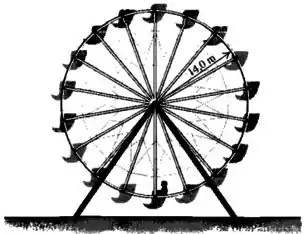
Questão 7
Um volante circular como raio 0,4 metros gira, partindo do repouso, com aceleração angular igual a 2rad/s².
a) Qual será a sua velocidade angular depois de 10 segundos?
b) Qual será o ângulo descrito neste tempo?
c) Qual será o módulo vetor aceleração resultante?
Ver solução completaQuestão 8
No instante , uma partícula parte com velocidade angular de em trajetória circular de raio e sofre uma desaceleração de até parar. Determine:
- O número de voltas que ela realiza;
- O tempo de movimento;
- A aceleração tangencial.
Questão 9
Um corpo rígido gira em torno de um eixo fixo com velocidade angular constante quando, a partir do instante , passa a ter uma aceleração angular constante de módulo e sentido oposto ao da velocidade angular. Denotando por o tempo gasto pelo corpo para sua velocidade angular atingir o valor nulo e por o seu deslocamento angular do instante até o instante , podemos afirmar que
- e ;
- e ;
- e ;
- e ;
- e ;
Questão 10
Dois carros percorrem uma pista de corrida circular no mesmo sentido. O carro A viaja com rapidez constante de . O carro B parte do repouso e sua rapidez cresce a uma taxa constante até atingir . Quando o carro B tem a mesma rapidez que o carro A, é sempre verdade que:
(A) o carro B está ultrapassando o carro A.
(B) o carro B tem mesma aceleração tangencial que o carro A.
(C) o carro B tem mesma aceleração radial que o carro A.
(D) o carro B tem mesma aceleração que o carro A.
(E) o carro B percorreu uma distância maior do que A.
Ver solução completaQuestão 11
Um volante de raio igual a parte do repouso e se acelera com aceleração angular constante
de . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante
a) no início;
Ver solução completaQuestão 12
Um volante de raio igual a parte do repouso e se acelera com aceleração angular constante
de . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante
b) depois de ele ter girado um ângulo de ;
Ver solução completaQuestão 13
Um foguete é lançado de um ângulo do topo de uma torre com altura . Devido ao design das engrenagens, suas coordenadas são da forma e onde e são constantes. Além disso, a aceleração do foguete após o lançamento é . Use a origem do eixo de coordenadas como a base da torre.
(d) Qual é o vetor posição do foguete após o seu lançamento?
Ver solução completaQuestão 14
Um disco horizontal roda em torno de um eixo vertical que passa pelo seu centro. O disco está inicialmente rodando a uma velocidade angular de e tem uma aceleração angular constante de . Quantas voltas o disco dá até estar momentaneamente em repouso?
Questão 16
Um disco que gira com velocidade angular é freado uniformemente com desaceleração angular até atingir o repouso. Durante a frenagem ele executa uma revolução. Outro disco, idêntico ao primeiro, tem velocidade angular é freado com uma desaceleração . O número de revoluções que ele executa até atingir o repouso é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 17
Uma roda de raio 0,5 metros rola sem deslizar sobre uma superfície horizontal, como mostrado na figuraabaixo. Começando a partir de repouso, a roda se move com aceleração angular constante de .
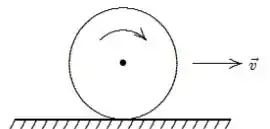
A distância percorrida pelo centro da roda no intervalo de tempo de t = 0 a t = 2s é:
- Zero
- Nenhuma destas.
Questão 18
Um disco que gira com velocidade angular é freado uniformemente até atingir o repouso. Durante afrenagem ele executa uma revolução. Outro disco, idêntico ao primeiro, tem velocidade angular é freado com mesma desaceleração que o primeiro. O número de revoluções que ele executa até atingir orepouso é:
Questão 19
A hélices de sustentaçãoo de um helicóptero, quando em movimento, descrevem uma área circular de . Supondo-se que começam a girar a partir do repouso e em atingem a velocidade de , o valor da velocidade angular da hélice e o da velocidade tangencial de um ponto na sua extremidade serão, respectivamente,
e
e
e
e
e
Ver solução completaQuestão 21
Considere a seguinte expressão para o vetor aceleração linear de uma partícula de um corpo rígido em rotação em torno de um eixo fixo: , onde é vetor posição da partícula com relação ao eixo de rotação, é o vetor velocidade linear da partícula, é o vetor velocidade angular de rotação, e é o vetor aceleração angular. Tendo em mente o movimento e a trajetória da partícula, marque a alternativa incorreta ( significa módulo de ):
A. Na expressão da aceleração, o termo é ortogonal ao termo .
B. O termo do vetor aceleração é responsável por fazer variar .
C. O termo do vetor aceleração é responsável por fazer variar .
D. O termo do vetor aceleração é responsável por alterar a direção do vetor .
E. O termo do vetor aceleração é responsável por alterar a direção do vetor .
Ver solução completaQuestão 22
Dois pontos estão localizados sobre uma roda rígida que está girando com uma velocidade angular decrescente em torno de um eixo fixo perpendicular aos raios da roda e que passa pelo centro de massa. O ponto está localizado no aro da roda e o ponto está localizado a meio caminho entre o eixo e o ponto . Qual das seguintes afirmações referentes a esta situação é necessariamente verdadeira?
a) Ambos os pontos têm a mesma aceleração centrípeta
b) Ambos os pontos têm a mesma aceleração tangencial
c) Ambos os pontos possuem a mesma velocidade angular instantânea
d) A cada segundo, o ponto gira de um ângulo maior que o ponto , na trajetória de cada um
e) Ambos os pontos possuem a mesma velocidade linear instantânea
Ver solução completaQuestão 25
Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:
onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .
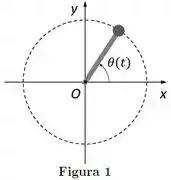
Qual é a aceleração centrípeta da partícula no instante inicial , sabendo que o raio da circunferência que ela descreve é ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 26
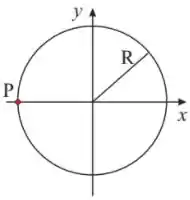
Q - Uma partícula percorre, em sentido horário, uma trajetória circular de raio , como na figura ao lado. Ao passar pelo ponto , mostrado na figura, o vetor aceleração total da partícula, em unidades do sistema internacional, é dado por
.
Considerando que a componente tangencial do vetor aceleração total seja constante, o módulo da velocidade da partícula segundo após ela passar pelo ponto P é:
Questão 27
Um disco de massa m e raio r, inicialmente parado, alcança uma velocidade após completar duas revoluções com uma aceleração angular constante. Qual sua aceleração angular?
a)
b)
c)
d)
e)
Ver solução completaQuestão 28
Uma partícula descreve um movimento de trajetória circular de raio . A aceleração dessa partícula é dada por , onde é uma constante positiva, a velocidade angular varia com o tempo e os vetores e são os unitários nas direções radial e tangencial ao movimento. Qual a única incorreta das frases a seguir?
(a) O módulo da velocidade linear é constante durante o movimento.
(b) O vetor velocidade é sempre perpendicular ao vetor posição.
(c) A partícula leva cada vez menos tempo para dar uma volta completa no círculo definido pela sua trajetória.
(d) O vetor velocidade não é perpendicular ao vetor aceleração.
Ver solução completaQuestão 29
Um carretel gira em torno de seu eixo central com velocidade angular . Existe atrito com o eixo, que produz uma aceleração angular .
a) Obtenha o instante de tempo no qual o carretel para de girar.
b) No instante inicial encontre o módulo da aceleração total de um ponto na borda do carretel cuja distância ao eixo é .
Ver solução completaQuestão 30
Um corpo rígido gira em torno de um eixo fixo com uma aceleração angular constante. Quais das seguintes afirmações é verdadeira a respeito da aceleração tangencial de qualquer ponto do corpo?
(A) ela é igual à aceleração centrípeta;
(B) seu módulo é zero ;
(C) ela depende da velocidade angular;
(D) ela depende da variação da velocidade angular;
(E) ela é constante em módulo e direção;
Ver solução completaQuestão 31
Para que uma amostra de sangue em uma centrífuga com de raio seja submetida a uma aceleração centrípeta de , a centrífuga deve atingir uma velocidade de:
A.
B.
C.
D.
E.
Ver solução completaQuestão 32
6 - Encontre a aceleração resultante instantânea de uma partícula se movendo em um círculo de raio , se a velocidade angular instantânea for de e a aceleração tangencial for de . Expresse o ângulo do vetor aceleração resultante em relação ao vetor de velocidade tangencial.
- a
- a
- a
- a
- a
Questão 33
A posição angular de um ponto da borda de uma roda que gira em torno de seu centro é dada por , onde está em radianos e em segundos.
Quantas voltas tal ponto dá em torno do centro da trajetória circular entre os instantes e ?
Questão 34
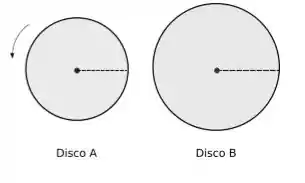
A figura mostra dois discos que podem girar em torno de seus centros independentemente. No instante , as retas de referência dos dois discos têm a mesma orientação (como mostrado no desenho); o disco já está girando com uma velocidade angular constante e o disco parte do repouso com uma aceleração angular constante de.
(a) Em que instante as duas retas de referência têm o mesmo deslocamento angular ?
(b) Qual será o primeiro instante , após , para o qual as duas retas de referência estão paralelas com a linha que une o centro dos dois discos?
(c) Considere agora que o deslocamento angular do disco varia no tempo com , onde está em radianos. Em qual instante a velocidade angular de é igual à velocidade angular de ?
Questão 35
Um volante de raio igual a parte do repouso e se acelera com aceleração angular constante
de . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante
c) depois de ele ter girado um ângulo de .
Ver solução completaQuestão 36
Um disco que girava em torno de seu eixo de simetria com velocidade angular constante começa a ser freado com desaceleração angular uniforme até atingir o repouso. No processo em que ele é freado ele completa exatamente uma volta de seu movimento.
Um outro disco, idêntico ao primeiro, mas que possui velocidade angular inicial começa a ser freado com mesma desaceleração angular que o primeiro. Quantas voltas completas em torno de seu eixo esse segundo disco dá até atingir o repouso?
(a) 25
(b) 10
(c) 5
(d) 2
(e) 1
Ver solução completaQuestão 37
Um toca-discos com um prato de diâmetro é posto em rotação por meio de uma correia ligada ao eixo de um motor de diâmetro . Veja a ilustração abaixo. Partindo do repouso, o prato alcança a velocidade angular final (rotações por minuto) em um intervalo de tempo Considere a correia como sendo inextensível e suponha as acelerações constantes. Resolva o problema literalmente para só no final substituir os valores numéricos.
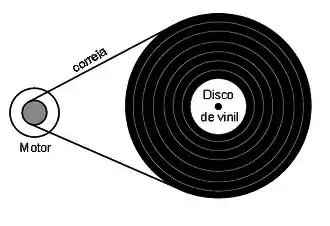
(a) Determine as acelerações angulares do motor e do prato do toca-discos.
(b) Determine quantas rotações o prato faz até atingir sua velocidade final.
(c) Determine os módulos das acelerações radial ar e tangencial at de um ponto na borda do prato após ele atingir a velocidade final.
Ver solução completaQuestão 38
Um corpo inicialmente em repouso, é acelerado em uma trajetória circular de raio , segundo a equação . Sabe-se que a partícula passa pela posição em . Determinar:
(b) A posição angular do corpo em função do tempo;
Ver solução completaQuestão 39
O ponto P na figura indica a posição de um corpo que se move com rapidez decrescente em sentido horário em uma trajetória circular. Qual vetor melhor representa a direção da aceleração do corpo no ponto P?
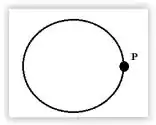

Questão 40
O motor de uma centrífuga de raio é acionado no instante de tempo , conferindo à extremidade da centrífuga uma aceleração cuja componente tangencial é constante e igual à . Supondo que em a centrífuga esteja em repouso, qual é o intervalo de tempo que o motor deve permanecer acionado para que a centrífuga adquira uma velocidade angular de rev?
(Dica: revrad. Use essa transformação para encontrar a sua resposta!)
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 41
Um corpo se desloca ao longo de uma pista curva de tal modo que o módulo de sua velocidade é maior quanto mais baixo ele se encontra, como representado na figura ().
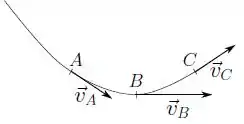
Escolha a opção que melhor representa o vetor aceleração instantânea nos pontos A, B, C.
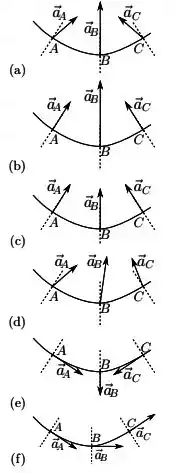
Questão 42
(Cap 4 – Ex 56) Um viciado em aceleração centrípeta executa um movimento circular uniforme de período e raio . No instante , a aceleração é Quais são, nesse instante, os valores de
(a) e
(b) ?
Ver solução completaQuestão 43
O disco A, de 10 cm de raio, é acoplado por uma correia ao disco B, cujo raio vale 25 cm. O disco A aumenta sua velocidade angular, a partir do repouso, a uma taxa uniforme de 1,6 rad/ . Supondo que a correia não deslize, qual das seguintes afirmações não é verdadeira?

A) A aceleração tangencial na borda de A é igual a aceleração tangencial na borda de B.
B) A aceleração centrípeta na borda de A é diferente da aceleração centrípeta na borda de B. C) A velocidade angular de A é diferente da velocidade angular de B.
D) A rapidez na borda de A é igual a rapidez na parte reta da correia.
E) O módulo do vetor aceleração em um ponto na borda de A é igual ao módulo da aceleração em um ponto na borda de B.
Ver solução completaQuestão 44
Uma caixa encontra-se sobre um carrossel, a uma distância do eixo de rotação. Inicialmente todo o sistema encontra-se em repouso. No instante o motor do carrossel é ligado e sua velocidade angular aumenta linearmente com o tempo, até atingir um valor máximo no instante , conforme mostrado na figura. Depois disso, a velocidade angular permanece constante neste valor máximo. Suponha que a caixa não escorregue em nenhum momento.
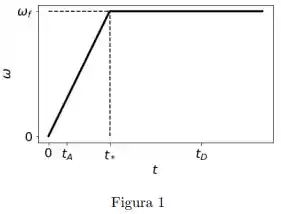
Considere os instantes de tempo e mostrados na figura e analise as seguintes afirmações:
() A aceleração tangencial da caixa em é não nula.
() A aceleração centrípeta da caixa em é não nula.
() A aceleração tangencial da caixa em é não nula.
Das afirmações acima, são verdadeiras apenas:
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 45
Questão 2
A órbita elíptica de um pequeno satélite orbitando um planeta esférico é mostrada na figura. Em que ponto sobre a órbita a velocidade linear do satélite é máxima?

Questão 46
41. Uma bola homogênea de raio rola sem deslizar, a partir do repouso, desde o topo de um domo hemisférico de raio .
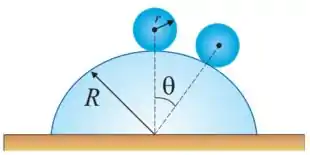
(a) Depois de percorrer que ângulo em relação à vertical a bola deixará a superfície?
Ver solução completaQuestão 47
Um carro, considerável como uma partícula, sobre uma lombada circular de centro de curvatura em , como indica a figura. O módulo da velocidade do carro vai diminuindo à medida que ele sobe a lombada. Dadas as setas identificadas pelos números , , , e da figura, a que pode representar a aceleração do carro o ponto da subida indicado é a número
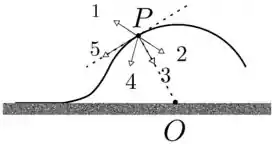
Questão 48
43. Para um disco de massa e raio , que rola sem delizar, o que é maior, sua energia cinética translacional ou sua energia cinética de rotação em relação ao centro de massa?
(a) A energia cinética de rotação em relação ao centro de massa é maior.
(b) A resposta depende da massa do disco.
(c) As duas energias são iguais
(d) A resposta depende do raio do disco.
(e) A energia cinética translacional é maior.
Ver solução completaQuestão 49
Em um treinamento, um veículo é colocado em uma pista circular e percorre a cada . sabendo que o diâmetro da pista é , podemos afirmar que o módulo da aceleração centrípeta do veículo, em , é igual a
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 50
Q - Uma partícula desloca-se sobre um círculo de raio com vetor velocidade que varia com o tempo segundo a equação onde . Podemos afirmar que quando a partícula encontra-se na posição angular , o módulo do vetor aceleração, em , é:
Ver solução completaQuestão 51
Um disco de raio executa um movimento circular, cuja velocidade angular decresce uniformemente. Considere dois pontos e , o ponto sendo localizado na borda do disco, e o ponto sendo localizado a uma distância do centro do disco. Assinale a opção INCORRETA
(a) A aceleração centrípeta do ponto é igual ao triplo da do ponto .
(b) As frequências dos pontos e são iguais.
(c) O módulo da aceleração tangencial do ponto é o triplo da do ponto .
(d) A velocidade linear do ponto é o triplo da do ponto
(e) A velocidade angular instantânea dos pontos e são iguais.
Ver solução completaQuestão 52
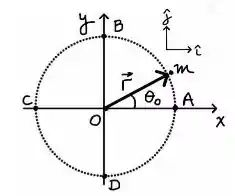
Uma partícula de massa está na ponta de uma haste fina que pode girar em torno de um eixo fixo perpendicular ao plano , passando por sua origem. A partícula pode descrever um movimento circular (linha pontilhada) descrito pelo ângulo com o eixo , orientado positivamente no sentido anti-horário. No instante , a partícula encontra-se parada em (vide figura), quando a haste começa a se mover com aceleração angular constante
Seja o vetor aceleração de , onde e são os vetores unitários nas direções , respectivamente. Quando a partícula passa pelo ponto A pela primeira vez e satisfazem:
- e
- e
- e
- e
- e
- e
- e
- e
- e
Questão 53
A partir do gráfico da figura abaixo, da velocidade angular em função do tempo, qual das seguintes afirmações é verdadeira à respeito da aceleração angular e do deslocamento angular em cada segmento?
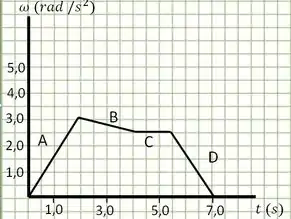
I. No segmento A; ,
II. No segmento B; ,
III. No segmento C; ,
IV. No segmento D; ,
A. Somente IV;
B. Somente I;
C. Somente I e IV;
D. Somente I e III;
E. Somente II e III;
Ver solução completaQuestão 55
[ENUNCIADO COMUM ÀS QUESTÕES 1 E 2]
Uma roda de raio está inicialmente em repouso. Partindo do instante a roda é acelerada a até atingir uma velocidade angular de num tempo . Em a aceleração cessa.
[QUESTÃO 1]
Sejam e respectivamente as acelerações tangencial e radial de um ponto na borda da roda imediatamente após . Podemos afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 56
[ENUNCIADO COMUM ÀS QUESTÕES 1 E 2]
Uma roda de raio está inicialmente em repouso. Partindo do instante a roda é acelerada a até atingir uma velocidade angular de num tempo . Em a aceleração cessa.
[QUESTÃO 2]
A distância percorrida por um ponto da borda do disco durante a aceleração é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 57
Na figura podemos observar o movimento de três partículas, num certo instante . Todas elas deslocam-se no sentido anti-horário sobre círculos de raio , com velocidades variáveis (direção e/ou módulo). Nestes instantes aparecem, indicados nas figuras, também os vetores aceleração e seus módulos. Em cada um dos instantes assinalados na figura, achar os vetores velocidade e aceleração.