Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Gráficos do Movimento Retilíneo

Ver Todos os Exercícios

Teoria

Uma parte importante na cinemática é a análise de gráficos, são bem comuns as questões abrangendo esse tipo de conhecimento.

Tudo que faremos a seguir parte das seguintes afirmações:

  • A função posição de um corpo é a integral da função velocidade;
  • A função velocidade é a derivada da função posição e também é a integral da função aceleração
  • A função aceleração é a derivada da função velocidade

Derivada?? Integral? Vou ter que usar isso? Isso é Cálculo!

Calma meu caro Watson! Não vamos ter que estudar nem usar isso, não nesse tópico de física. Essas informações que coloquei são apenas para você saber que tudo que vou falar a partir de agora tem uma base, não é mágica ou porque eu quero que seja haha.

Pela primeira afirmação, vamos poder dizer que a variação da posição é igual a área sob o gráfico da v   x   t .

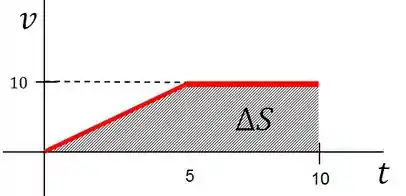
Fazendo a área sob o gráfico acima, vamos obter a variação da posição do objeto entre t = 0   a t = 10   s

Pela segunda afirmação, como a velocidade é a integral da aceleração, similar a posição, podemos descobrir a variação da velocidade fazendo a área sob o gráfico a   x   t

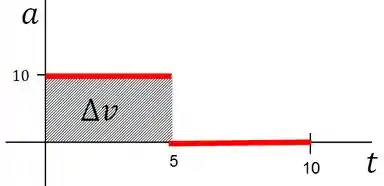
O gráfico mostra que a variação da velocidade entre t = 0   a t = 5   s é igual entre t = 0   a t = 10   s , pois a área sob o gráfico é a mesma nos dois intervalos. O que confirma com tudo que aprendemos até agora, porque a aceleração é zero entre t = 5   s   e t = 10   s se aceleração é zero, a velocidade não varia e por isso a variação de 0   a   5   s é igual de 0   a   10   s .

Ainda pela segunda afirmação, podemos relacionar o gráfico da posição no tempo com a velocidade da seguinte forma:

A velocidade é a tangente do gráfico S   x   t , um detalhe importante é que se fizermos a tangente de um ponto obtemos a velocidade instantânea naquele instante.

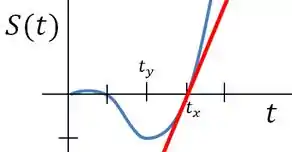
A reta vermelha representa a reta tangente do ponto 0 ; t x . A tangente dessa reta é igual a velocidade instantânea no instante t = t x

Agora, se pegarmos dois pontos e traçarmos uma reta entre eles e fizermos a tangente dessa reta, obteremos a velocidade média do objeto no trajeto de um ponto ao outro.

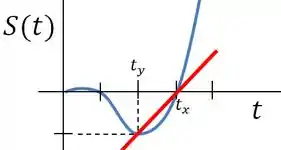
Neste caso estamos calculando a velocidade média entre os instantes t = t y a t = t x

Lembrete: dificilmente acharemos o ângulos que a reta forma com o eixo t , vamos usar a relação

T g θ = c a t e t o   o p o s t o c a t e t o   A d j a c e n t e

Vamos estudar a última afirmação agora, devido a ela podemos dizer que a aceleração é a tangente do gráfico v   x   t

Do mesmo modo que acabamos de fazer para a velocidade, se fizermos a tangente de um ponto no gráfico v   x   t obteremos a a aceleração instantânea do objeto.

Se traçarmos uma reta por dois pontos e calcularmos a tangente dessa reta estamos calculando a aceleração média do objeto.

Pronto, é isso que temos que saber analisar nos gráficos de cinemática, sem Cálculo, apenas áreas e tangentes. Vamos treinar então!

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 32-04

A figura mostra a aceleração a t de um chihuahua que persegue um pastor alemão sobre um eixo. Em qual dos períodos de tempo indicados o chihuahua se move com velocidade constante?

Passo 1

Para descobrirmos o momento que o cachorro está com velocidade constante basta, vermos no gráfico o período de tempo onde a aceleração é zero, pois como a aceleração é a tangente da velocidade, sempre que a velocidade for constante a reta tangente estará na horizontal e por isso a aceleração será zero.

Assim, no instante de tempo E   temos o momento de velocidade constante, caracterizando um movimento retilíneo uniforme.

Observe que os períodos C   e G   que poderiam causar dúvidas, pois a aceleração é constante representa o movimento retilíneo uniformemente variado, já que a aceleração é constante e diferente de zero.

Resposta

Intervalo E

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 32-03

A figura mostra a velocidade de uma partícula que se move em um eixo x . Determine a o sentido inicial e b o sentido final do movimento. c A velocidade da partícula se anula em algum instante? d A aceleração é positiva ou negativa? e A aceleração é constante ou variável?

Passo 1

Precisamos analisar o gráfico v   x   t   para obter as informações pedidas, nos itens a e b   ele quer o sentido e para isso vamos analisar a equação da velocidade

v = Δ S Δ t

Como Δ t   é sempre positivo, temos que o sinal da velocidade está diretamente relacionado com o sentido do movimento e por isso no item a a velocidade inicial é negativa, temos que o objeto move-se no sentido negativo e no item b a velocidade final é positiva, então o objeto move-se no sentido positivo.

Passo 2

c   A velocidade vai ser zero, se em algum instante a linha do gráfico cruzar o eixo do tempo, olhando o gráfico vemos que existe um momento em que a linha cruza o eixo do tempo e por isso: sim, a velocidade será zero em algum instante de tempo.

Passo 3

d Temos que aceleração é a tangente do gráfico v   x   t , sendo assim como o ângulo θ (ângulo entre a reta e o eixo do tempo) no gráfico acima é menor que 90 ° temos que a tangente desse ângulo é positiva, assim a aceleração é positiva.

Passo 4

e Seguindo o raciocínio do item anterior, vemos que o ângulo θ não muda ao longo do gráfico o que nos garante que a aceleração é constante. Podiamos pensar também que como a velocidade varia uniformemente ( varia de forma linear –uma reta- ) o movimento é uniformemente variado e por isso a aceleração é constante.

Resposta

a Sentido negativo

b Sentido Positivo

c Sim.

d Positiva

e   Constante

Exercício Resolvido #3

UFPE 2004

O gráfico da velocidade em função do tempo de um ciclista, que se move ao longo de uma pista retilínea, é mostrado a seguir. Considerando que ele mantém a mesma aceleração entre os instantes t = 0 e t = 7 segundos, determine a aceleração e a distancia percorrida neste intervalo de tempo. Expresse sua resposta no SI

Passo 1

Bom, a questão pelo gráfico nos deu a Velocidade Final, a Velocidade Inicial e o tempo! Com isso já podemos calcular a aceleração né? É só lembrar que

a = ∆ V ∆ t = V - V 0 ∆ t = 12 - 4 4 = 8 4 = 2 m / s 2

a = 2 m / s 2

Show!

Passo 2

E agora que a gente tem a aceleração fica MUUUITO fácil de calcular a distância, né? É só usarmos a formulinha do sorvetão! Como a quetão quer em t=7, simbora:

∆ S = V 0 t + a t 2 2

∆ S = 4.7 + 2 . 7 2 2

∆ S = 77 m

Lindíssimo!

Resposta

a = 2 m / s 2 e ∆ S = 77 m

Exercício Resolvido #4

UFPE 2005

A figura mostra um gráfico da velocidade em função do tempo para um veículo que realiza um movimento composto de movimentos retilíneos uniformes. Sabendo-se que em t = 0 a posição do veículo é   x 0 = +50 km, calcule a posição do veículo no instante t = 4,0h em km.

Passo 1

A gente tem o gráfico da velocidade pelo tempo e a questão quer o delocamento em 4 horas. Puts... E agora? Já pensou? ISSO, a área do gráfico da velocidade em função do tempo dá o deslocamento! Show demaisss!

Então vamos por partes:

De 0 a 1h: Temos um retângulo, com área de 15km

De 1h a 2h: Temos um deslocamento nulo

De 2h a 4h: Temos um retângulo, com área de -40km

Então nosso deslocamento total vai ser a soma disso tudo!

∆ S = 15 + 0 - 40 = - 25 k m

Mas nossa posição inicial, como a questão nos diz, era 50km, então estamos em:

50 - 25 = 25 k m

Showwww!

Resposta

25 k m

Exercício Resolvido #5

UNESP 2005

O gráfico na figura descreve o movimento de um caminhão de coleta de lixo em uma rua reta e plana, durante 15s de trabalho.

a) Calcule o deslocamento neste intervalo de tempo.

b) Calcule a velocidade média do veículo

Passo 1

A questão pede pra gente calcular o deslocamento no intervalo de tempo mostrado, e para isso basta a gente calcular a área embaixo da curva. Mas calma aí, não precisa sair integrando nada não, aqui vamos usar um método mais simples.

Vamos olhar cada figura do gráfico e calcular as áreas usando geometria simples, no fim somando-se todas as áreas teremos o deslocamento no intervalo de 15s.

Passo 2

Vamos seguindo com o nosso plano, o primeiro ponto é analisar o gráfico.

Aqui teremos 3 áreas.

A 1 t r i â n g u l o   d a   e s q u e r d a = b . h 2

Repara que cada quadradinho conta como uma unidade, sendo assim onde não houver marcações conte quadradinhos.

A 1 = 3.8 2 = 12 m

Pra área do meio temos um trapézio.

A 2 t r a p é z i o = B + b . h 2

Lendo o gráfico tiramos os valores e calculamos a segunda área:

A 2 = 4 + 2 . 12 2 = 36 m

Por ultimo terceira área:

A 3 t r i â n g u l o   d a   d i r e i t a = b . h 2

A 3 = 2.12 2 = 12 m

Por fim:

S = ∑ A = 12 + 36 + 12 = 60 m

Passo 3

Agora só falta encontrarmos a velocidade média e para isso é só dividir o espaço calculado pelo intervalo de tempo, faremos isso então senhoras e senhores.

V = ∆ S ∆ t = 60 15 = 4 m / s

Mais um exercício pra conta!

Resposta

  1. 60m
  2. 4m/s

Exercício Resolvido #6

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 38-69

Quando uma bola de futebol é chutada na direção de um jogador e o jogador a desvia de cabeça, a aceleração da cabeça durante a colisão pode ser relativamente grande. A figura mostra a aceleração a t   da cabeça de um jogador de futebol sem e com capacete, a partir do repouso. No instante t = 7,0   m s , qual é a diferença entre as velocidades da cabeça sem e com capacete ?

Passo 1

O problema quer a diferença entre as velocidades no tempo t = 7   m s , sabemos qua ambas as analises avelocidade inicial é v 0 = 0   , assim se fizermos a variação de velocidade entre t = 0   e t = 7   m s vamos obter a velocidade em t = 7   m s já que a velocidade inicial é zero.

Passo 2

Então primeiro vamos obter a variação da velocidade entre t = 0   e t = 7   m s quando o jogador não está usando capacete. Para isso vamos calcular a área sob o gráfico.

Δ v = á r e a = A 0 - 2   + A 2 - 4   + A 4 - 6   + A 6 - 7  

Δ v = 120.2 2 + 140 + 120 . 2 2 +   200 + 140 . 2 2 + 200.1 2 . 10 - 3

Δ v = 120 + 260 + 340 + 100 . 10 - 3

v 7 - v 0 = 0,820   m / s  

v 7 = 0,820   m / s    

Passo 3

Agora vamos calcular a área sob o gráfico para o jogador que está usando o capacete

Δ v = 40.3 2 + 40.1 + 80 + 40 . 2 2 + 80.1 2 . 10 - 3  

v 7 - v 0 = 60 + 40 + 120 + 40 . 10 - 3

v 7 = 0,260   m / s  

Passo 4

Agora temos que fazer a diferença entre a velocidade da cabeça do jogador com e sem capacete.

Δ v = 0,820 - 0,260

Δ v =   0,560   m / s    

Resposta

Δ v = 0,56   m / s

Exercício Resolvido #7

UNESP 1999

O gráfico na figura mostra a posição x de um objeto, em movimento sobre uma trajetória retilínea, em função do tempo t. A partir desse gráfico, é possível concluir que a velocidade instantânea do objeto anulou-se somente

a) no instante 0 segundo.

b) nos instantes 9 e 14 segundos.

c) nos instantes 2 e 7 segundos.

d) nos instantes 5 e 11 segundos.

e) nos instantes 2,5,7 e 11 segundos.

Passo 1

Temos um gráfico de espaço, certo?. Entao para termos a velocidade do objeto temos que derivar isso, lembra? Uma coisa que a gente aprende lá em calculo 1 é que os pontos em que a derivada (que é o mesmo que a velocidade nesse caso) é 0 são os pontos extremos ou picos do gráfico, porque a inclinação da reta tangente é nula! E temos isso nos intantes 2, 5, 7 e 11, sacou? :D

Resposta

e) nos instantes 2,5,7 e 11 segundos.

Exercício Resolvido #8

UFRJ-2015.1-1ª prova- Física 1

Uma partícula descreve um movimento retilíneo. No gráfico, está representada a componente da velocidade desta partícula ao longo da trajetória como função do tempo. No instante t = 0   s , a partícula está na posição x = 0   c m . Assinale a afirmativa correta:

a A velocidade da partícula no instante t = 0   s vale v x = 0   c m / s ;

b A aceleração da partícula no instante t = 2,5   s vale a x = - 1   c m / s 2 ;

c O deslocamento da partícula no intervalo entre t = 0   e t = 2   s vale Δ x = 2   c m ;

d A posição da partícula no instante t = 2   s é x = 0   c m ;

e Nenhuma das respostas anteriores é correta.

Passo 1

Vamos ver alternativa por alternativa!

Alternativa a :

Essa já podemos eliminar de cara! Podemos ver no gráfico que, no instante t = 0   s , a velocidade é v x = 1   c m / s .

Passo 2

Alternativa b :

Agora ele falou da aceleração da partícula no instante t = 2,5   s .

Repare que do tempo t = 2   s ao tempo t = 3   s , a velocidade da partícula é constante ( v x = - 1   c m / s ), logo nesse espaço de tempo a aceleração é nula!

Então no instante t = 2,5   s , a aceleração é a x = 0 ≠ - 1   c m / s 2 .

Logo, a alternativa está errada.

Passo 3

Alternativa c :

Vamos ver qual é a posição da partícula no tempo t = 2   s .

No espaço de tempo entre t = 0 e t = 2   s , a velocidade diminui de v x = 1 pra v x = - 1   c m / s . Então a aceleração média é:

a m = Δ v Δ t = - 1 - 1 2 - 0 = - 2 2 = - 1   c m / s 2

E o gráfico é uma linha reta nesse espaço de tempo, então a aceleração é constante! Logo, nesse espaço de tempo a partícula segue um MRUV, com a = - 1   c m / s 2 .

Passo 4

Num MRUV, a posição da partícula em função do tempo é dada por:

x t = x ( 0 ) + v 0 t + a t 2 2

Aqui temos x 0 = 0   c m ,   v 0 = 1   c m / s e a = - 1   c m / s 2 , então

x t = 0 + t - t 2 2

⇒ x 2 = 2 - 4 2 = 2 - 2 = 0   c m

Ou seja, no tempo t = 2 , a partícula volta pra onde estava no começo:

Δ x = 2 - 2 = 0 ≠ 2   c m

Logo, a alternativa c está errada.

Passo 5

Alternativa d :

Como acabamos de ver, em t = 2   s   a posição da partícula é 0   c m .

Então a alternativa é verdadeira.

Então alternativa e é falsa, já que a d   é a verdadeira :)

Resposta

Alternativa d

Exercícios de Livros Relacionados

Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b