Movimento Retilíneo Uniformemente Variado
Produzido por Ludovic BeghinTeoria
O movimento retilíneo uniformemente variado, para os íntimos MRUV, é um movimento no qual a aceleração
O MRUV recebe esse nome porque sua velocidade vai variar linearmente com o tempo, então a aceleração que vamos usar aqui vai ser a aceleração média:
Esse movimento pode ocorrer de duas formas:
- Movimento Acelerado: Ocorre quando a aceleração tem mesma direção e sentido da velocidade e assim a velocidade sempre aumenta com o tempo.
- Movimento Retardado: Ocorre quando a aceleração tem direção e sentido contrários da velocidade, fazendo com que a velocidade diminua com o tempo.
Agora vamos ao que interessa! As fórmulas o MRUV! 😉
Fórmulas do Movimento Retilíneo Uniformemente Variado (MRUV)
Existem três fórmulas principais no movimento retilíneo uniformemente variado, o que vai determinar a escolha da fórmula são as informações que o enunciado te dá!
Função horária da velocidade
Essa é a equação mais básica do MRUV, na prática ela é a equação da aceleração média com a velocidade em evidência:
Onde:
é a velocidade final do objeto; é a velocidade inicial; é a aceleração, e; é o tempo.
É muito importante a gente entender também o gráfico de
A equação que descreve
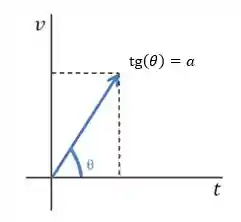
Função horária da posição
Essa equação descreve a posição do objeto em função do tempo:
Onde:
é a posição final do objeto, e; é a posição inicial
A função horária da posição vai ser útil quando você não tiver a velocidade inicial!
Equação de Torricelli
A equação de Torricelli é uma equação que relaciona a velocidade com a variação da posição, sem depender do tempo, o que é bem importante, pois em muitos problemas o tempo não será informado e você deverá usar esta equação para resolvê-los:
Onde,
MRUV: Vídeo Aula
Agora se liga nesse vídeozinho super completo que o Responde Aí preparou pra você sobre Movimento Retilíneo Uniformemente Variado 👇
Prontinho... agora é só praticar bastante com os exercícios 😉