Movimento Bidimensional Relativo
Teoria
Fala aí, seja muito bem vindo ao Responde Aí! Hoje a gente vai bater um papo sobre movimento bidimensional relativo!
-Como assim, bidimensional relativo? 😖
Sempre que estamos estudando o movimento de um corpo consideramos um referencial, por exemplo, na imagem abaixo o carro
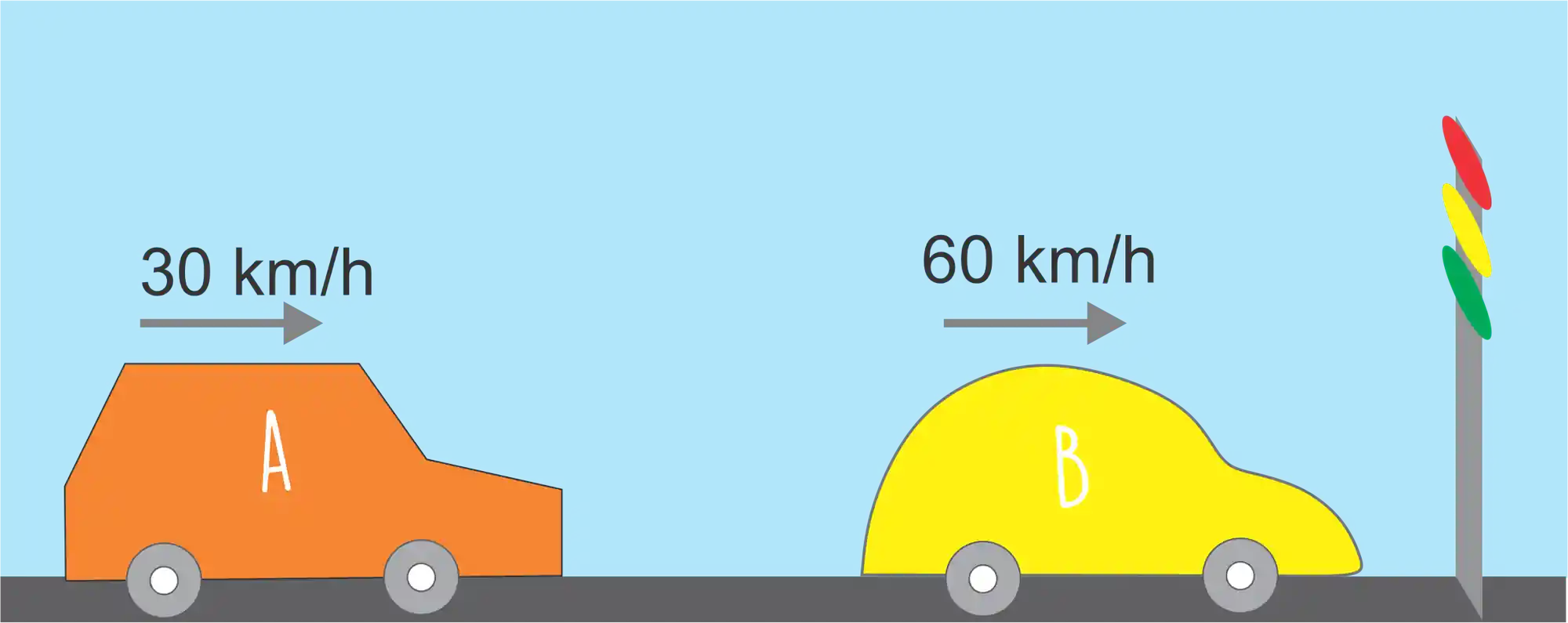
Se usarmos o carro
Na figura acima os carrinhos estavam se movendo apenas em relação a
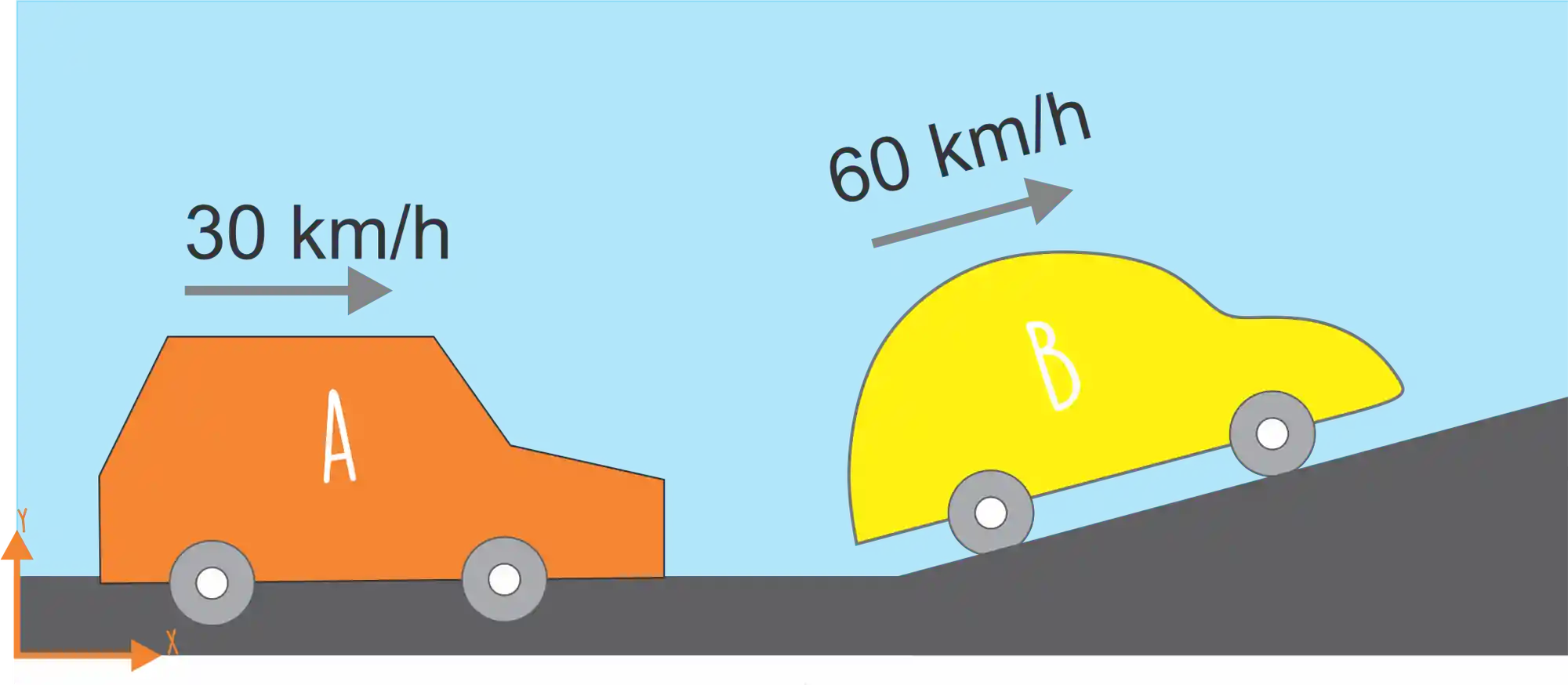
O movimento começa a variar em
📢 Clique para saber mais:
- Movimento Bidimensional Relativo: Exercícios Resolvidos
- Fórmulas do Lançamento Oblíquo
- Fórmulas do Movimento Retilíneo Uniformemente Variado
- Movimento Relativo Unidimensional
Posição Relativa
O vetor posição relativa do objeto
Também podemos escrever em termos de vetores unitários, assim:
Você também pode conferir esse conteúdo em vídeo:
Velocidade Relativa
O vetor velocidade relativa entre
Onde
Aceleração Relativa
A aceleração relativa entre
Onde
Agora vamos praticar com exercícios?
Velocidade Relativa
Aceleração Relativa
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Um ônibus (ônibus 1) trafega com velocidade em relação a Terra. Outro ônibus (ônibus 2) se aproxima do ônibus 1 com velocidade de , também em relação à Terra.
- Qual a velocidade do ônibus 1 em relação ao ônibus 2?
- Qual é, aproximadamente, o módulo dessa velocidade?
Passo 1
Fala aí! Vamo lá?
Pra achar a velocidade do ônibus 1 em relação a o ônibus 2, temos que diminuir a velocidade do ônibus 1 pela velocidade do ônibus 2! Show, então:
Lindíssimooo!
Passo 2
Agora pra calcularmos o módulo desse vetor é só usarmos aquela regrinha que aprendemos em vetores, né?
Então, no nosso caso, temos:
Conseguimos! Show!!
Resposta
Exercício Resolvido #2
UFF
Um ciclista trafega com velocidade em relação a um observador em repouso no solo. Outra ciclista, que trafega com rapidez no sentido negativo do eixo x, observa o primeiro. Qual a velocidade do primeiro ciclista no referencial da segunda?
Passo 1
Fala aí! Vamo nessa?
Nós temos a velocidade de dois ciclistas e queremos encontrar a velocidade de um ciclista em no referencial da outra (que está em movimento). Pra mudar de referencial é bem simples, lembra? É só subtrairmos pela velocidade do novo referencial que tá em movimento. Ou seja:
Como a questão nos diz, é 4m/s no sentido negativo de x, ou seja:
Portanto, ficamos com:
Conseguimos! Show de bolinhas!
Resposta
Exercício Resolvido #3
PUC-RIO – 1ª Prova – 2012.2
Observe a figura e leia atentamente o texto:
No instante , um carro, dirigido por Bruno , se encontra na esquina de um cruzamento enquanto que outro carro, dirigido por Ângela , está em uma rua a da esquina. Bruno viaja para Norte (eixo ) enquanto Ângela viaja para o Leste (eixo ). Em relação ao solo, as velocidades de Ângela e Bruno são constantes e têm mesmo módulo de .
Escreva o vetor velocidade de Ângela em relação a Bruno .
Encontre o vetor posição de Ângela em relação a Bruno , em função do tempo.
Qual é a aceleração relativa de Ângela em relação a Bruno?
Passo 1
Utilizando a fórmula de velocidade relativa temos que:
Substituindo os dados sem esquecer-se de explicitar a direção das velocidades:
Passo 2
Como é constante, temos:
As posições iniciais foram dadas, e . Portanto . Assim:
Passo 3
Como é constante, então .
Resposta
Exercício Resolvido #4
UFRJ-Física 1- 1ª Prova-2014.1
Vista de um referencial fixo nas escretas e centrado no Sol, a Terra tem vetor velocidade dado em um certo instante por e um foguete em translação tem velocidade constante , como mostra a figura. Considerando o foguete como um referencial com eixos coordenados , , e de mesmas direções e sentidos que os respectivos eixos , e , o vetor velocidade da Terra relativo a ele é
Passo 1
Nesse caso temos uma situação levemente diferente do que estamos acostumados, mas fique tranqüilo que é quase igual.
Como a terra está se mexendo, e o foguete também, iremos considerar o referencial deles dois como sendo o Sol. Essa é a única mudança. Os dados do problema são
Pela fórmula de velocidade relativa
Resposta
Letra
Exercício Resolvido #5
PUC-RIO – Física B - 1ª Prova – 2013.2 – letra c - Modificada
Um navio está ao norte e a leste do navio . O navio está navegando com uma velocidade constante de na direção sul; o navio navega com uma velocidade constante de em direção ao norte do leste.
Escreva uma expressão para o vetor posição de em relação à em função do tempo considerando o instante como o instante e que os navios estão nas posições iniciais descritas acima. (Sugestão: faça um desenho para orientá-lo na sua solução posicionando o navio na origem do sistema de coordenadas em ).
Dados:
Passo 1
Antes de começar a calcular o vetor posição, vamos primeiro fazer um desenho esquemático. Desenhar é a melhor forma de não se confundir e de visualizar tudo que está acontecendo.
Agora podemos calcular o vetor posição!
Passo 2
Para calcular o vetor posição do navio em relação ao navio , devemos relembrar da fórmula de movimento relativo, temos que:
Onde e o vetor posição do navio em relação ao navio . e são os vetores posição dos navios e respectivamente.
Para determinar , devemos primeiro achar o vetor posição de cada navio em relação ao mar.
Passo 3
Vamos primeiro calcular o vetor posição do navio . Para facilitar, iremos trabalhar com as componentes e . Então, vamos lá!
Como o navio não possui movimento horizontal, temos que a componente do vetor posição é:
Em , temos uma velocidade que aponta no sentido negativo, dessa maneira, nosso vetor posição será:
Ou seja, o vetor posição do navio será:
Passo 4
Vamos agora calcular o vetor posição do navio . Para determinar o vetor posição de cada componente, devemos decompor a velocidade.
Em :
Como o navio se encontra na origem, o vetor posição será dado apenas pela componente da velocidade vezes o tempo.
Em :
Ou seja, o vetor posição do navio será:
Passo 5
Agora que temos o vetor posição de ambos os navios, podemos calcular .
Resposta
Exercício Resolvido #6
USP – 1ª Prova – 2014
Duas partículas e se movem ao longo do eixo e , respectivamente, com velocidades constantes e . Em elas estão nas posições: , .
Esboce a situação descrita acima no plano no instante .
Escreva algebricamente (usando versores indicados no enunciado) o vetor posição de cada uma das partículas.
Determine o vetor que representa a posição relativa da partícula com respeito à partícula , como função do tempo.
Determine o vetor velocidade relativa entre essas duas partículas.
Passo 1
Colando as partículas em suas posições iniciais temos:
Passo 2
Vamos usar a equação da posição para determinar a posição de cada partícula.
Para a partícula temos:
Como e
Aplicando o mesmo método para , temos:
Passo 3
O vetor velocidade relativa da partícula em relação a partícula é encontrado fazendo . Analogamente, o vetor posição relativa da partícula 2 em relação a partícula 1 pode ser encontrado fazendo , Logo:
Passo 4
Como já foi dito no item anterior, basta fazer :
Resposta
Exercício Resolvido #7
USP – 1ª Prova – 2015
Duas partículas estão restritas a mover-se no plano . O movimento destas partículas é descrita pelas funções posição , , e , onde a posição é medida em metros e o tempo em segundos. Considere a direção na horizontal e na vertical.
Determine os vetores posição e de cada partícula e o vetor posição relativa .
Para ,faça um esquema no plano cartesiano dos vetores posição e e do vetor posição relativa . Determine a distância entre as partículas.
Determine o(s) tempo(s) para o(s) qual(is) as duas partículas colidem.
Determine a velocidade relativa, , no(s) instante(s) no(s) qual(is) as partículas colidem.
Passo 1
Os vetores e são encontrados pela própria definição, onde a posição corresponde a componente , e a posição corresponde a componente .
Para a o ficará:
E para o fica:
Já o vetor posição relativa é obtido pela fórmula do movimento relativo:
Agora basta fazer a subtração de com e de com :
Passo 2
Substituindo para os vetores que encontramos no item anterior ficamos com:
Para representar estes vetores no plano cartesiano, basta indicar as coordenadas do ponto que encontramos para e desenhar uma seta da origem até o ponto.
Agora só falta determinar a distância entre as partículas. Mas caramba, nós já temos isso! É o que posição relativa quer dizer. Posição relativa é a distância relativa às duas partículas.
Só que temos a distância relativa em forma de vetor, precisamos dar um valor para essa distância, que é justamente o comprimento desse vetor, ou seja, o módulo do vetor distância relativa. Basta utilizar a fórmula para encontrar o módulo de um vetor:
Lembrando que .
Passo 3
Vamos pensar. No item anterior nós descobrimos que a distância entre as partículas é o vetor posição relativa. E qual a distância entre as partículas quando elas colidem? Isso mesmo, se elas estão colidindo então a distância é zero. Logo, o vetor posição relativa tem que ser igual a zero.
Portanto, as duas componentes do vetor têm que ser iguais a zero.
e
Temos que para e , a primeira equação é satisfeita. No entanto, apenas para que a segunda equação é satisfeita. Daí, apenas para há colisão.
Passo 4
Lembrando que a velocidade nada mais é que a derivada do vetor posição. Basta derivarmos o vetor posição relativa, desta maneira:
Para derivar um vetor, basta derivar apenas as componentes:
Que resulta em:
Agora substituindo o instante que achamos para a colisão no item anterior, , temos:
Resposta
;
;
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 90-82
Um rio de 200 m de largura corre com uma velocidade uniforme de através de uma floresta, na direção oeste. Um explorador deseja sair de uma pequena clareira na margem sul e atravessar o rio em um barco a motor que se move com uma velocidade escalar constante de em relação à água. Existe uma outra clareira na margem norte, rio acima a partir de um ponto da margem sul, exatamente em frente à clareira. Em que direção o barco deve ser apontado para viajar em linha reta e chegar à clareira da margem norte? Quanto tempo o barco leva para atravessar o rio e chegar à clareira?
Passo 1
Primeiro vamos desenhar o que o problema que temos, para entendermos mlhor o que está acontecendo. Esse seria um esboço com o sdados que ele no deu.
Vamos resolver essa questão usando o vetor posição relativa. Cosiderando que o barquinho está na origem do nosso eixo no porto sul.
Vamos enterder primeiro o que faremos. A linha tracejada significa a linha reta que o barquinho deve andar para chegar do porto sul até o porto norte.
A seta azul escuro simboliza o deslocamento da água em relação ao porto sul. A seta vermelha o deslocamento do barco em relação ao porto sul e a seta amarela o deslocamento do barco em relação a água , ou seja, a pra onde o barco deve ser apontado.
Passo 2
Temos então e quer chegar na posição . Ambas posições são em relação a origem no porto sul (referêncial parado). Logo o deslocamento do barquinho seria
Passo 3
Sabemos que a água desloca-se com velocida , pela equação da posição descobrimos
Passo 4
Vamos então calcular o vetor posição relativa do barco em relação a água pela equação
Terminamos de descobrir a equação para o vetor posição do barco em relação a água, porém ela está em função do tempo e por isso vamos primeiro descobrir o valor de .
Passo 5
Como o problema também nos fornecer o módulo da velocidade do barco em relação a água .
Pela equação da posição de um movimento uniforme temos:
Como temos o módulo do vetor velocidade e pelo tempo ser sempre positivo podemos dizer que
Tirando a raíz
Passo 6
Substituindo na equação do vetor posição temos:
Com esse vetor já temos representado a direção em que o barco deve ser apontado, porém se quisermos completar a resposta podemos dar o ângulo que o barco deve ser apontado em relação a margem sul do rio.
Como é horizontal (mesma direção da margem), temos que o ângulo entre os dois vetores é igual ao ângulo de com a margem sul.
Já vimos uma fórmula para calcular ângulo entre vetores, que é
Resposta
Exercício Resolvido #9
UFMS
Um carro move-se com velocidade constante de 60 km/h. Começa a chover e o motorista observa que as gotas de água da chuva caem formando um ângulo de 30° com a vertical. Considerando que, em relação à Terra, as gotas caem verticalmente, qual a velocidade em que as gotas de água caem em relação ao carro?
a) 30√3 km/h.
b) 60 km/h.
c) 120 km/h.
d) 30 km/h.
e) 80km/h.
Passo 1
Vamos entender o que tá rolando por aqui, temos o carro seguindo com velocidade e a chuva caindo com uma velocidade .
A velocidade da chuva é caindo perpendicular à terra, mas o motorista vê a velocidade da chuva em relação ao carro . Aqui temos um caso de velocidade relativa bidimensional, podemos resolver encontrando e fazendo:
E a partir daqui tirar o módulo do vetor , ou simplesmente usar um pouco de trigonometria pra calcular direto pela figura o módulo dessa velocidade, e é o que faremos.
Passo 2
Para calcular vamos usar um pouco de trigonometria aqui, vamos desenhar o triângulo com a velocidade do carro ali fechando ele
Como sabemos lá da trigonometria:
No nosso caso:
Resposta
c) 120 km/h.