Lançamento Oblíquo
Teoria
O lançamento oblíquo acontece quando um objeto é arremessado formando um ângulo em relação à horizontal.
Confere esse vídeo que o Responde Aí preparou pra você aprender tudo o que precisa saber sobre lançamento oblíquo para resolver todos os exercícios! 👇
📢 Clique para saber mais:
- Fórmulas do lançamento Oblíquo
- Lançamento Oblíquo: Exercícios Resolvidos;
- Lançamento Vertical;
- Movimento uniformemente variado.
´
Como Calcular o Lançamento Oblíquo?
Pra a gente aprender como funcionam os cálculos em problemas envolvendo lançamento oblíquo, vamos começar imaginando um caso qualquer!
Imagine que em condições ideais, sem vento e sem resistência do ar, um operador de canhão deseja que seu projétil atinja a porta de um castelo a uma certa distância
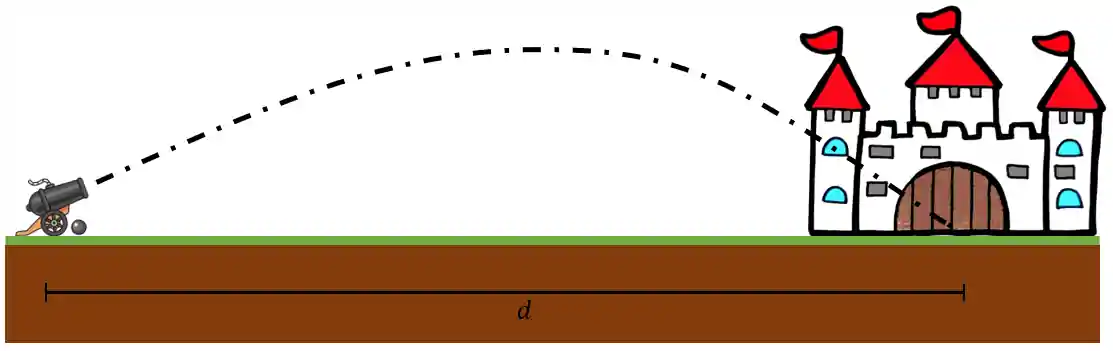
Qual deve ser a velocidade inicial desse tiro de bala de canhão para que ele acerte o alvo??? Como podemos fazer para calcular isso??
Vamos dar um zoom no canhão:
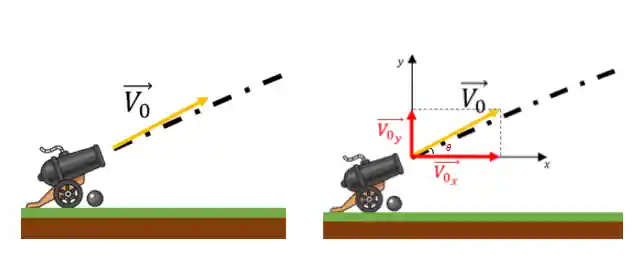
A nossa bala de canhão tem um velocidade inicial
Pra resolver problemas de lançamento oblíquo, precisamos olhar separadamente pro movimento vertical e pro movimento horizonta usando as relações trigonométricas.
Assim, podemos escrever:
Agora, bora entender melhor como fazemos isso?
Movimento Horizontal
Vamos começar pensando no movimento do eixo
Na horizontal não temos nenhum tipo de aceleração, estamos falando de um movimento uniforme, então podemos escrever a seguinte fórmula:
Onde
Podemos relacionar a velocidade inicial do projétil
Movimento Vertical
Quando olhamos para o movimento na vertical, percebemos pela trajetória da bala de canhão que na primeira metade do movimento a bola de canhão está subindo, e que na segunda metade do movimento ela começa a cair novamente em direção ao solo.
Isso acontece por causa da gravidade!
Então, como no movimento vertical existe a atuação da aceleração da gravidade, para resolver as questões associadas ao eixo
- Função horária da posição (Sorvetão):
- Equação da Velocidade:
- Equação de Torricelli:
📢 OBS: Fique atento! Todos os termos que tem a gravidade apareceram com o sinal negativo nas fórmulas de MRUV, porque temos que considerar que a gravidade aponta no sentido contrário do que orientamos o eixo
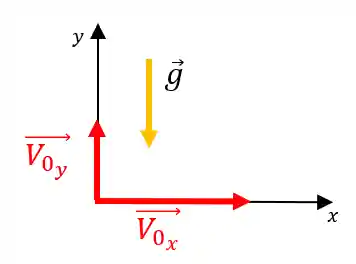
Agora, vamos praticar com exercícios?!
Como Calcular o Lançamento Oblíquo?
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP-1ª Prova-2014.1
Um navio de guerra tenta bombardear simultaneamente dois navios A e B. Se os projéteis são disparados com velocidades cujas magnitudes são idênticas e seguem as trajetórias mostradas na figura abaixo, qual dos navios é atingido primeiramente? Despreze a resistência do ar
A.
B.
Os dois são atingidos simultaneamente.
Mais informação é necessária para se responder esta questão.
Nenhuma das alternativas é correta
Passo 1
A questão quer saber qual dos dois projéteis tem menor tempo de voo.
Vamos olhar a equação do tempo de voo para um lançamento oblíquo:
Vemos que o tempo de voo depende da velocidade inicial, do ângulo que esta faz com o eixo e da aceleração da gravidade. Como a aceleração da gravidade e a velocidade de lançamento é a mesma para os dois projéteis o tempo de voo vai depender exclusivamente do ângulo
Quanto maior for maior será o tempo de voo, por isso o projétil que ficará menos tempo no ar será aquele com menor ângulo que é o canhão
Resposta
Letra
Exercício Resolvido #2
PUC-RIO-1ª Prova-2013.2
Um canhão lança suas balas com uma certa inclinação em relação à horizontal. Assuma que a bala atinge o chão na mesma elevação em que foi lançada.
Se o tempo de voo foi de segundos, qual a componente vertical de sua velocidade inicial?
(Considere )
50
nenhuma das anteriores
Passo 1
Pra começar bem a gente precisa entender a situação o canhão atira uma bala com uma inclinação em relação a horizontal e velocidade . O enunciado diz pra gente considerar que a bala chega no chão na mesma altura que foi lançada, é como se desprezássemos a altura do canhão.
Vamos então desenhar um esquema pra ver o que tá rolando ali.
O problema quer que a gente encontre a componente vertical daquela velocidade , e nos dá o tempo de voo. Esse tempo de voo é simplesmente o tempo marcado pro percurso da bala sair do canhão e chegar no chão de novo.
O que vamos fazer aqui é trabalhar pensando só no movimento vertical da bala, olhando só a componente da velocidade.
Como nos foi dado o tempo de voo, podemos considerar que a bala demora o mesmo tempo pra subir e pra descer, sendo assim até atingir a altura , o tempo é.
Passo 2
E agora é só a gente aplicar a equação da velocidade para o eixo vertical pensando na subida, olhando apenas pra velocidade .
Onde pro movimento de subida.
E o que vai acontecer quando a bala atingir a altura máxima? A velocidade dela será 0, e aí a relação vai ter essa cara.
Considerando que temos:
Resposta
Alternativa .
Exercício Resolvido #3
UNICAMP-1ª Prova-2014.2
Um canhão, posicionado sobre um terreno completamente plano, dispara um projétil com um velocidade inicial de módulo fazendo um ângulo de com a horizontal. Considerando a posição incial do canhão como origem do sistema de coordenadas e a aceleração da gravidade determine:
O tempo total de voo do projétil.
O vetor posição do projétil quando o mesmo atinge sua altura máxima.
O vetor velocidade quando o mesmo atinge o solo.
Considere agora que o projétil deva atingir um alvo que está a uma distância de do canhão. Qual deve ser o ângulo de tiro para que o projétil com velocidade inicial de módulo possa atingir o alvo?
Passo 1
Para calcular o tempo de voo, basta aplicar a equação de tempo de voo
Substituindo os valores que temos no enunciado
Passo 2
A componente do vetor posição será a altura máxima, certo? E pela simetria de um lançamento oblíquo podemos dizer que quando o projétil está na altura máxima a componente da posição éa metade do alcance, lembra?
Então vamos primeiro encontrar a altura máxima, sua fórmula é:
Passo 3
Só falta achar o alcance, e faremos isso usando a equação pro alcance que aprendemos
Como nossa componente em é metade do alcance, temos que
Agora que temos nossa componente em e nossa componente em , podemos escrever o vetor posição.
.
Passo 4
O problema que o vetor velocidade no final do movimento, sabemos que durante qualquer instante do movimento permanece constante. Já varia durante todos os instantes, mas no final do movimento temos que
Primeiro vamos achar decompondo a velocidade, usando a regra do COlado/Separado
Agora calcularemos usando a mesma regra
Como vimos que no final a velocidade em é
Passo 5
Nesse item nós foi dado o alcance desejado e o problema quer sabe que ângulo fará com que alcancemos essa distância de
Basta aplicarmos a equação do alcance e termos
Fazendo isso vamos encontrar dois valores para
Resposta
Exercício Resolvido #4
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 88-76
Um projétil é lançado do nível do chão com uma rapidez inicial de . Encontre o ângulo de lançamento ( o ângulo que a velocidade inicial forma acima da horizontal) de forma que a altura máxima do projétil seja igual ao seu alcance horizontal. (Ignore a resistência do ar.)
Passo 1
Vamos entender o problema fazendo um desenho da situação, o projétil é lançado com velocidade e o problema pede o ângulo de inclinação para que o alcance e a altura sejam iguais, dessa forma temos a seguinte situação.
Beleza, se eu sei disso agora preciso encontrar uma relação entre a altura e o alcance , vamos fazer isso decompondo a velocidade e analisando os dois movimentos, vertical e horizontal.
Passo 2
Vamos decompor as velocidades, usando as seguintes relações:
E aqui separamos os movimentos, o movimento horizontal é um movimento uniforme e portanto o alcance é dado por:
Aonde é o tempo total do movimento, isso é, até o projétil chegar ao solo.
Já o movimento vertical é um pouquinho diferente, temos a gravidade desacelerando, portanto temos um movimento uniformemente variado. Pra encontrar a altura máxima, podemos aplicar a equação de torricelli.
Só que aqui a velocidade no ponto da altura máxima é e portanto:
Isolando e lembrando que
Agora é só igualar as equações para esses carinhas aqui:
Cortando os termos semelhantes temos o seguinte:
Putz, mas e esse aí, o que eu faço com ele?
Ele é o tempo total do lançamento, e é o único termo que a gente não tem.
Muita calma nessa hora, vamos dar um jeitinho nisso.
Passo 3
Para encontrarmos o tempo vamos analisar o movimento vertical, se a gente pensar na subida poderemos ver pela equação da velocidade quem é esse cara:
Onde
Já que o movimento completo leva em consideração subida e descida. Aqui sabemos também que na altura máxima a velocidade final na vertical é e então a equação fica:
Rearrumando temos então o querido tempo!
Agora é só voltar na nossa equação antiga e substituir essa galera aí:
Daí pegue a tesoura pois cortaremos muita gente por aqui hehe!
Cortando e de ambos os lados e também o que passará a ser , temos:
E se liga aí, essa relação que temos é a tangente!
Agora é só inverter e já era:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 86-34
Uma bola de futebol é chutada a partir do chão com uma velocidade inicial de e um ângulo para cima de . No mesmo instante um jogador a de distância, na direção do chute, começa a correr para receber a bola. Qual deve ser sua velocidade média para que alcance a bola imediatamente antes que toque o gramado?
Passo 1
O problema quer saber qual deve ser a velocidade do jogador para que ele alcance a bola. Para determinarmos a velocidade do jogador precisamos saber o quanto ele vai correr, ou seja, o alcance da bola e quanto tempo ele vai correr que seria o tempo de voo da bola.
Como ainda não sabemos o alcance da bola o jogador pode estar dentro desse alcance e aí ele teria que correr no sentido da bola. Ou fora do alcance e aí sua velocidade apontara para o sentido oposto. Como não temos o tempo percorrido vamos inicialmente adotar a hipótese do jogador fora do alcance da bola, só pra gente fazer um desenho.
A partir daí vamos calcular o tempo de voo da bola e com isso o alcance, pra enfim definirmos a velocidade do jogador.
Passo 2
Pra calcularmos o tempo de voo vamos analisar apenas o movimento vertical da bola, pra isso a gente precisa decompor a velocidade na componente vertical.
Agora a gente pode usar a equação da velocidade, vamos analisar a subida da bola e para ela a equação fica:
Quando a bola sobe ela vai perdendo velocidade por causa da gravidade e atinge no ponto máximo, sendo assim:
Substituindo e , temos o tempo:
E não podemos esquecer que o tempo de subida é só metade do tempo do movimento, temos que usar o tempo total que é o dobro desse aqui pra analisar o alcance.
Passo 3
Vamos agora calcular o alcance da bola, no eixo não temos aceleração e por isso o alcance é dado por:
E lembrando que a velocidade em é:
Então o alcance fica:
Então o nosso desenho estava certinho, o jogador está a 55 metros da bola e precisa correr na direção oposta.
Passo 4
Agora que temos tudo basta substituir na equação da posição do movimento uniforme para descobrirmos a velocidade do jogador
A velocidade negativa significa que o jogador correrá no sentido oposto do movimento da bola e portanto a hipótese que adotamos estava correta pro movimento.
Resposta
Exercício Resolvido #6
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 90-103
Você assiste seu amigo jogando hóquei. Durante o jogo, ele atinge o disco de tal forma que, ao chegar no seu ponto mais alto, o disco passa de raspão por cima do muro de acrílico de de altura que cerca o campo, distante do jogador. Encontre a componente vertical da velocidade inicial, o tempo para atingir o muro e a componente horizontal da velocidade inicial, a rapidez inicial e o ângulo de lançamento. (Ignore a resitência do ar.)
Passo 1
Temos que descobrir quanto vale a componente da velocidade inicial. Por ser um lançamento oblíquo temos que
O problema ainda nos deu a altura máxima , pela equação da altura máxima conseguiremos relacionar altura com a velocidade em
Podemos reescrevê-la da seguinte forma
Substituindo por
Passo 2
Agora queremos descobrir o tempo de subida. Que é metade do tempo de voo. Assim, temos:
Podemos escrever da seguinte forma também
Substituindo na equação o valor da componente da velocidade inicial que terminamos de encontrar, termos
Passo 3
O problema que saber agora a componente da velocidade inicial, decompondo a velocidade
Vamos agora analisar o alcance que ainda não usamos para nada, pela fórmula do alcance temos
Usando a relação trigonométrica
Podemos reescrever a equação da seguinte forma
Substituindo pelos dados que temos (obs: o problema nos fornece )
Passo 4
Agora que temos a componente e a componente da velocidade inicial, basta fazer o módulo do vetor velocidade para achar a rapidez inicial.
Passo 5
Podemos achar o ângulo de diversas formas, vamos optar por calcular por
Na calculadora:
Resposta
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 86-28
Uma partícula é lançada de uma catapulta no instante , com uma velocidade inicial de módulo e um ângulo de acima da horizontal. Quais são os módulos das componentes horizontal e vertical do deslocamento da pedra em relação à catapulta em ? Repita os cálculos para as componentes horizontal e vertical em e para as componentes horizontal e vertical em .
Dados:
Passo 1
O problema quer a componente(horizontal) e (vertical) da posição de uma partícula em uma dado instante de tempo.
Então para resolver uma questão assim, nada melhor que achar a equação da posição para cada eixo e depos apenas substituir o valor de tempo desejado.
Passo 2
Enão vamos aos dados do problema, é um lançamento com e velocidade inicial , isso é um lançamento oblíquo.
Vamos analisar o movimento em cada eixo, começando pelo eixo . Que sabemos que executa um movimento uniforme e por isso a única equação que temos é
Vamos considerar a posição de lançamento sendo a origem e por isso e como o movimento é uniforme temos que
Onde vamos achar pela regra do “COlado/Separado”
Substituinda na equação da posição do movimento uniforme temos:
Passo 3
Agora, vamos analisar o movimento no eixo . Por se tratar de um lançamento sabemos que a partícula vai sofrer ação da aceleração da gravidade. Assim a equação da posição é
Calcularemos pela regra do “COlado/Separado”
Substituindo na equação da posição e lembrando que a partícula sai da origem
Passo 4
Agora que temos a equação da posição para o eixo e eixo , podemos resolver os itens.
Queremos saber a componente da posição no instante
Passo 5
Deseja-se saber a componente da posição no instante
Passo 6
Queremos saber a componente da posição no instante
Passo 7
Deseja-se saber a componente da posição no instante
Passo 8
Queremos saber a componente da posição no instante
Passo 9
Deseja-se saber a componente da posição no instante
Resposta
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 86-27
Um certo avião tem uma velocidade de e está mergulhando com um ângulo abaixo da horizontal quando o piloto libera um chamariz. A distância horizontal entre o ponto de lançamento e o ponto onde o chamariz se choca com o solo é . Quanto tempo o chamariz passou no ar? De que altura foi lançado?
Passo 1
É um problema de lançamento oblíquo, onde a questão nos deu o alcance, a velocidade inicial e o ângulo q a velocidade faz com o eixo .
Porém é um exercício um pouco diferente do comum, pois o ângulo dado está abaixo do eixo e o lançamento não é para cima. Mas, pode ficar tranquilo a resolução é igual.
Passo 2
Queremos saber quanto tempo que o chamariz passou no ar, ou seja, o tempo que ele gastou para percorrer no eixo .
Por isso, pela equação do movimento em
Vamos decompor a velocidade pela regra do “COlado/Separado”
Passando a velocidade em para , teremos:
Agora podemos substituir na equação da posição
Passo 3
Agora que temos o tempo de voo, precisamos apenas da equação da posição do movimento em
Precismos achar e para isso vamos usar a regra do “COlado/Separado”
Passando a velocidade para
Substituindo na equação
Observe que a velocidade é negativa pois o lançamento é para baixo, logo é negativa. Agora substituindo o tempo que encontramos temos
Resposta
Exercício Resolvido #9
UNICAMP-1ª Prova-2013.2
Dois canhões apontam-se mutuamente, como mostrado na figura, e disparam suas balas no mesmo instante de tempo. O canhão dispara sua bala com velocidade de módulo , e o canhão com velocidade . As distâncias no problema são .
Qual a aceleração de cada uma das balas após o disparo?
Quanto tempo se passou a partir do momento do disparo até o instante da colisão? A que altura acontece a colisão?
Se não houvesse o canhão , qual seria o alcance da bala do canhão A?
Passo 1
As balas realizam lançamentos oblíquos. Estão sujeitas apenas a aceleração da gravidade, ou seja,
Passo 2
Com a origem no ponto e o ângulo entre a inclinação do canhão e a horizontal, pelas fórmulas do lançamento oblíquo de alcance e do eixo , temos:
Logo quando acontece a colisão temos que , assim obtemos que:
Fazendo :
Portanto:
Ou seja, a colisão acontece a de altura.
Passo 3
Como já que o triângulo na figura é isósceles, temos o alcance máximo:
Resposta
;
Exercício Resolvido #10
UFRJ-Física 1-1ª Prova-2012.2
Um projétil é lançado com velocidade formando um ângulo com a horizontal. O ponto de lançamento está localizado a uma altura acima do solo. A figura mostra o sistema de referencia fixo, que está localizado no solo e tem eixo vertical alinhado verticalmente com o ponto de lançamento. De acordo com este referencial, pressupondo que a resistência do ar é desprezível e que a Terra é um referencial Inercial:
Escreve os vetores posição e velocidade , como funções do tempo , usando os unitários e dos eixos e , respectivamente, indicados na figura;
Calcule o tempo que o projétil leva para atingir a altura máxima;
Calcule o tempo de vôo do projétil.
Determine, quando o projétil toca o solo, o módulo da sua velocidade .
Passo 1
Vamos começar o problema escrevendo os dados do enunciado
Isso vai servir para conferirmos depois se as respostas estão de acordo com os dados do enunciado.
A gravidade é negativa, porque ela é para baixo, lembra? Cuidado com os sinais!!
Passo 2
Para escrevermos os vetores posição e velocidade, devemos achar a posição e velocidade ao longo do tempo do movimento ao longo de e ao longo de.
No eixo temos um Movimento Uniforme.
No eixo , temos um lançamento vertical, que neste caso é um lançamento vertical para cima.
A primeira coisa a fazer é encontrar e
Usando a “regra do COlado, SEparado” vamos ter
Ambos são positivos, porque a velocidade está para direita e para cima.
Passo 3
Vamos agora escrever as equações da posição pelo tempo, começando pelo movimento ao longo de
Passo 4
Para o movimento ao longo de
Passo 5
Lembra como escrevemos esse vetor agora?
Ele fica:
Passo 6
Vamos agora escrever as equações da velocidade pelo tempo, começando de novo pelo movimento ao longo de , como o movimento é uniforme temos que:
Logo,
Passo 7
Para o movimento acelerado ao longo de
Passo 8
O vetor velocidade representado por unitários fica da seguinte forma:
Passo 9
Ele quer o tempo que o projétil gasta para atingir a altura máxima. Isso vai acontecer quando a velocidade em é zero. Então devemos fazer
Passo 10
O tempo de vôo vai ser o tempo que ele demora para chegar ao chão. O que isso quer dizer?
Que o valor da posição na vertical é zero.
Resolvendo a equação de segundo grau
Como o tempo de vôo deve ser positivo, e o valor dentro da raiz é maior que
Passo 11
Para acharmos o módulo da sua velocidade devemos achar cada componente quando o tempo for igual ao tempo de vôo. Então
Passo 12
Agora que sabemos o valor de cada componente da velocidade podemos fazer módulos dela
Lembrando que
Resposta
Exercício Resolvido #11
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 90-115
Darlene é uma motociclista de circo. Como clímax de seu show, ela larga de uma rampa inclinada de , salta um fosso de largura e pousa em um rampa mais elevada (altura ) do outro lado . Para uma dada altura , encontre a mínima rapidez de largada necessária para ela realizar o salto com sucesso. Quanto vale para , e ?
Mostre que, independente da rapidez de largada, a altura máxima da plataforma é . Interprete fisicamente este resultado. (Despreze a resistência do ar e trate a motoqueira e a moto como se fossem uma única partícula.)
Passo 1
O problema quer saber a velocidade mínima com que é possível realizar esse salto. Acharemos se acharmos a velocidade inicial a qual em um instante a moto tenha percorrido em e esteja na altura .
Pois se a moto tiver em uma altura menor que significa que ela não consegue fazer o salto e se altura for maior que ela não estava na velocidade mínima possível.
Passo 2
Vamos escrever a equação da posição no eixo
Lembrando que
Queremos o instante de tempo no qual a motociclista percorre a distância no eixo
Passo 3
Agora vamos estudar o movimento no eixo , escrevendo a equação da posição temos:
Como
Agora substituímos e
Como falamos no “passo 1” para achamos a velocidade mínima é preciso que o instante de tempo que a moto alcance a distância em ela esteja na posição em .
Como vimos que precisamos que isso ocorra no mesmo instante de tempo , basta substituirmos o valor de que achamos no “passo 2” para descobrirmos
Passo 4
Terminamos de achar uma equação para , então basta substituir os valores dados
Passo 5
Como raíz de um número negativo não existe no conjuto de números reais, se
Teriamos raíz de um número negativo o que não é possível. Se pensarmos no caso onde
teríamos uma divisão por zero e por isso a velocidade mínima iria tender ao infinito.
Então só é possível excutar esse salto se
Resposta
Exercício Resolvido #12
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 90-112
Um mergulhador salta de um penhasco em Acapulco, no México, acima da superfície da água. Neste momento, ele aciona sua mochila-foguete horizontamente, o que lhe dá uma aceleração horizontal constante de , sem efetuar seu movimento vertical. Quanto tempo ele leva até chegar à superfície da água? A que distância da base do penhasco ele atinge a água, suponto o penhasco vertical? Mostre que sua trajetória é uma linha reta. (Ignore a resistência do ar.)
Passo 1
Ao acionar a mochila-foguete o mergulhador passa a executar um movimento acelerado no eixo .
Com isso nada irá mudar quanto ao eixo , mas para resolver os itens que envolvam o movimento em iremos usar as equações do movimento uniformemente variado (MUV).
Passo 2
Para descobrirmos o tempo que o mergulhador gasta para chegar à água temos que analisar o movimento em , pois é pedido o tempo para o mergulhador sair da posição para chegar à água .
O problema não falou de nenhuma velocidade inicial no eixo e por isso, , temos que o movimento em é uma queda livre. Vamos usar as fórmulas do movimento acelerado pela gravidade
Passo 3
A distância em que o mergulhador atinge a água em relação a base do penhasco é o alcance do movimento no eixo .
O movimento no eixo é acelerado e por isso vamos usar a equação da posição do MUV
Considerando a base do penhasco como origem e visto que a velocidade inicial dele é zero, já que o mergulhador só aciona a mochila quando pula, temos
Substituindo por que foi o instante que o mergulhador chega à agua
Passo 4
Para mostrarmos qual a trajetória de algum objeto, o melhor método é achar a equação da trajetória.
Como é a posição da partícula no eixo e o representa o mesmo no eixo podemos chamar e
No item chegamos que
E no item encontramos que
Vamos sumir com o tempo e para isso vamos isolar na equação de
Substituindo esse valos na equação de chegamos
Essa é a equação da trajetória e podemos ver que ela é um polinômio do 1º grau e por isso representa uma reta .
Resposta
Exercício Resolvido #13
Elaboração Própria
Um jogador de futebol bate uma falta, fazendo com que a bola saia com velocidade inicial , do solo, fazendo um ângulo de . Sabendo que um vento sopra da esquerda para direita, imprimindo uma aceleração nessa direção com módulo igual ao módulo da gravidade. Determine a altura máxima do chute, e seu alcance. Na frente do jogador, a , está um gol com de altura. Determine se a bola vai na direção do gol, passa por cima dele, ou cai antes do gol.
Dados: , 
Passo 1
No enunciado, a bola é chutada para cima. Então:
No eixo , temos um lançamento vertical, que neste caso é um lançamento vertical para cima.
No eixo , nesse caso, temos aceleração então ele é um Movimento Uniformemente variado.
Pelo enunciado teremos:
Vamos primeiro achar as componentes da velocidade inicial, pela regra do “COlado/Separado”:
Passo 2
Para achar a altura máxima, estamos usando o movimento na vertical.
O que acontece quando a bola está na altura máxima? , como em temos um e queremos a posição, vamos usar a equação de Torricelli.
Passo 3
Para encontrarmos o alcance, primeiro devemos achar o tempo que ele demora para chegar ao chão, ou seja, quando
Resolvendo a equação do 2º grau, vamos encontrar dois valores para essa equação, mas lembre
O tempo não é negativo, TEMPO SEMPRE POSITIVO.
Passo 4
Agora usamos esse tempo na equação da posição do eixo . Lembrando que ele é um MUV
Passo 5
Para descobrir onde a bola passou, devemos achar a altura da bola quando ela passa pelo gol.
Primeiro vamos achar o tempo para ela chegar ao gol, saberemos isso pela posição do gol no eixo . Como temos o vento soprando para a direita, imprimindo uma aceleração constante de módulo igual à da gravidade, a gente tem
De novo caímos em uma equação do segundo grau. Resolvendo, e lembrando que
O tempo não é negativo, TEMPO SEMPRE POSITIVO.
A gente descobre que
Passo 6
Vamos agora descobrir a altura que a bola se encontra ao passar pela possição do gol.
A altura do gol é , como a bola passa a do chão, o jogador errou o chute no gol.
Repare que a aceleração do eixo não interfere em nada no movimento do eixo e vice versa.
Resposta
, ele erra o chute no gol.