Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Velocidade média

Ver Todos os Exercícios

Teoria

Fala aí, você chegou no Responde Aí. E aqui a gente vai te ensinar tudo sobre velocidade média.

O que é velocidade média?

A velocidade média é a razão entre a variação da posição e o intervalo de tempo.

Ou seja, é o tamanho da distância que você andou, divido pelo tempo que demorou pra você andar.

A fórmula de velocidade média é:

  • O é a distância percorrida.
  • O é o tempo que demorou para percorrer a distância.
  • E o é a velocidade média.

Como calcular a velocidade média?

Pra calcular a velocidade média, a gente só precisa saber o tamanho da distância, e o tempo que demorou para andar toda essa distância. Depois é só aplicar a fórmula da velocidade média.

Exemplo

Uma fámila está saindo de sua casa de praia e voltando para o interior. Às 15h o carro está a de distância da praia. Mais tarde, às 17h o carro está a de distância da praia. Qual a velocidade média desse carro?

Passo 1: A primeira coisa, é saber qual a distância percorrida, o nosso , pra isso é só subtrair a posição final menos a posição inicial.

Passo 2: O segundo passo é descobrir quanto tempo levou o movimento. Pra isso é só subtrair o tempo final menos o tempo inicial:

Passo 3: E agora é só a gente aplicar a fórmula da velocidade média!

Ou seja, a velocidade média desse carro é quilômetros por hora!

Unidades de medida de velocidade

No dia-a-dia, quando falamos de velocidade geralmente falamos de quilômetros por hora . Porém, quando a gente estuda física também usamos a unidade de metros por segundo .

As vezes uma mesma questão pode misturar as unidades de medida, então é bom você sempre lembrar que:

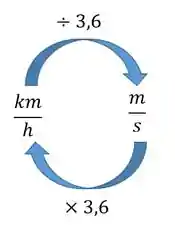
Pra não errar na hora da prova, a dica é sempre usar metros e segundos. E se precisar, no final você converte pra km/h!

Videoaula

Que saber mais sobre velocidade média? Então dá uma olhada nesse vídeo show:

Agora da uma olhadinha aqui em baixo, e dá uma olhada em todo o nosso conteúdo, exercícios e muito mais 👇

Como calcular a velocidade média?

Unidades de medida de velocidade

Videoaula

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 33-3

Durante um espirro, os olhos podem se fechar por até 0,50   s . Se você está dirigindo um carro a 90 k m / h e espirra, de quanto o carro pode se deslocar até você abrir novamente os olhos?

Passo 1

O enunciado nos forneceu o tempo que ficamos de olho fechados e a velocidade com que nosso carro está se movendo:

t = 0,5 s       v = 90 k m / h

Queremos descobrir a distância percorrida pelo carro, o Δ x .

Mas observamos que as unidades que ele nos forneceu não são equivalentes: o tempo está em segundos e a velocidade em quilômetros por hora.

Logo, devemos colocá-las no S . I . (Sistema Internacional de unidades). Assim, vamos dividir a velocidade por 3,6   para obtermos a velocidade em m / s :

v = 90 3,6 = 25 m / s

Passo 2

Agora, com os dados no S . I .   , conseguimos calcular o Δ x   :  

Δ x = 25   .   0,50

Δ x = 12,5   m

Assim, resolvemos o exercício: o carro desloca-se 12,5   m   enquanto você está de olho fechado.

Resposta

Δ x = 12,5   m

Exercício Resolvido #2

Mundo Educação Exercício Resolvido 4

Ao cobrar uma falta em um jogo de futebol, um jogador imprime à bola uma velocidade de 43,2 km/h. Sabendo que a bola gasta 3 s até atingir as redes, determine a distância percorrida.

a) 36 m

b) 48 m

c) 52 m

d) 75 m

e) 28 m

Passo 1

Fala aí! Bora pra mais essa?

Sabemos que pra gente calcular a distância percorrida, podemos usar a formulinha da velocidade média aqui ó:

v = ∆ S ∆ t

PORÉMMM, presta atenção nas unidades, jovem gafanhoto! A velocidade dada na questão tá em km/h e o tempo dado tá em segundos... Então o que nós fazemos? Isso, passamos de km/h pra m/s, e aí fica tudo na mesma unidade! Show, bora lá. Pra passar de km/h pra m/s basta a gente dividir tudo por 3,6, entao:

43,2 3,6 = 12 m / s

Foi!

Passo 2

Agora que temos tudo na unidade certinha, é só calcular o deslocamento! Então bora lá:

v = ∆ S ∆ t   → 12 = ∆ S 3

∆ S = 36 m

Finalizamosss!

Resposta

a) 36 m

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 9º ed. Rio de Janeiro, Exercício Resolvido 2

Um automóvel viaja em uma estrada retilínea por 40 km a 30 km/h. Em seguida, continuando no mesmo sentido, percorre outros 40 km a 60 km/h.

Qual é, aproximadamente, a velocidade média do carro durante este percurso de 80 km? (Suponha que o carro se move no sentido positivo de x.

Passo 1

Fala aí!

Pra gente calcular a velocidade média, a gente viu na teoria que:

v = Δ S Δ t

Como a gente tem dois trechos com velocidades diferentes, devemos aplicar a formulinha em cada um dos trechos pra descobrirmos o tempo total, nosso ∆ t . E como já sabemos o deslocamento total, fica fácil de calcular a velocidade média! Então:

No trecho 1:

v = Δ S Δ t   → 30 = 40 Δ t

Δ t = 1,33 h

Fazendo o mesmo no trecho 2, temos:

v = Δ S Δ t   → 60 = 40 Δ t

Δ t = 0,66 h

Show!

Passo 2

Agora que temos o tempo total e o deslocamento total, podemos calcular a velocidade média de todo percurso!

v = 80 ( 1,33 + 0,66 )   → 80 2 = 40 k m / h

Finalizamosss!

Resposta

v = 40 k m / h

Exercício Resolvido #4

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 84.4

Calcule a velocidade média nos seguintes casos:

  1. Você caminha 73,2m a 1,22m/s e depois corre 73,2m a 3,05m/s em uma pista reta
  2. Na mesma pista você caminha 1 min a 1,22m/s e depois corre 1 min a 3,05m/s

Passo 1

Pra gente calcular a velocidade média, a gente sabe que:

v = ∆ S ∆ t

Como a gente tem dois trechos com velocidades diferentes, podemos aplicar a formulinha em cada um dos trechos pra descobrirmos o tempo total, e como já sabemos o deslocamento total, fica fácil de calcular a velocidade média, né? Show! Bora lá:

No trecho 1:

v = ∆ S ∆ t   → 1,22 = 73,2 ∆ t

∆ t = 60 s

Fazendo o mesmo no trecho 2, temos:

v = ∆ S ∆ t   → 3,05 = 73,2 ∆ t

∆ t = 24 s

Prontinho!

Passo 2

Agora que temos o tempo total e o deslocamento total, podemos encontrar a velocidade média!

v = ∆ S ∆ t   → 2 x 73 , 2 24 + 60 = 1,743 m / s

Conseguimos!

Passo 3

Aqui na letra b é uma situação bem parecida, né? A diferença é que agora temos o tempo e queremos encontrar a deslocamento pra daí calcularmos a velocidade média! Como nossa velocidade tá em metros por segundo e o tempo em minutos, vamos utiluizar tudo em segundos. Vamo lá, dividindo em dois trechos novamente:

Trecho 1:

v = ∆ S ∆ t   → 1,22 = ∆ S 60

  ∆ S = 73,2 m

No trecho 2:

v = ∆ S ∆ t   → 3,05 = ∆ S 60

  ∆ S = 183 m

Passo 4

Agora ficou moleza pra calcular a velocidade média!

v = ∆ S ∆ t = 73,2 + 183 60 + 60 = 2,135 m / s

Resposta

  1. v = 1,743 m / s
  2. v = 2,135 m / s

Exercício Resolvido #5

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 9º ed. Cap 2 Problema 17

A posição de uma partícula que se move ao longo do eixo x é dada em centìmetros por x t = 9,75 + 1,50 t 3 , onde t está em segundos. Calcule a velocidade média (em cm/s) da partícula entre o intervalo de tempo de t=2s e t=3s.

Passo 1

E aí, meu consagrado! Bora pra mais uma?

Como a gente já tá CANSADO de ver, a gente sabe que:

v = ∆ S ∆ t =   S f - S i t f - t i

Bom, com o que a questão nos deu, logo de cara podemos calcular o ∆ t , né? Então:

∆ t = t f - t i = 3 - 2 = 1 s

Show! Mas e o deslocamento?

A gente tem a função do deslocamento da partícula, então é só a gente substituir o tempo de 2 e de 3 segundos e subtrair um do outro, assim teremos o quanto ele se movimentou entre esse intervalo de tempo! Show, bora lá então:

t = 2 s   → x t = 9,75 + 1,50 t 3   →   x t = 9,75 + 1,50 . 2 3 = 21,75 c m

t = 3 s   → x t = 9,75 + 1,50 t 3   →   x t = 9,75 + 1,50 . 3 3 = 50,25 c m

Pronto, agora já temos nossa distância final (3 segundos) e e inicial (2 segundos)! Podemos calcular o deslocamento tranquilo:

∆ S = S f - S i = 50,25 - 21,75 = 28,5 c m

Passo 2

Como a questão pediu a velocidade em cm/s, não precisamos converter nenhuma unidade. Agora que temos tudo certinho, é só jogar na formulinha!

v = ∆ S ∆ t   → v = 28,5 1

v = 28,5 c m / s

Conseguimossss! Show de bolinhas!

Resposta

v = 28,5 c m / s

Exercício Resolvido #6

UFAL

A posição de uma partícula (em metros) é dada em função do tempo (em segundos) pela seguinte equação x t = 5 t 3 - 8 t . A velocidade média entre os instantes t=1s e t=2s é:

  1. -35m/s
  2. 35m/s
  3. -27m/s
  4. 27m/s
  5. 0

Passo 1

Fala aí! Vamo nessa?

Bom, como a gente sabe, a velocidade média é calculada por:

v = ∆ S ∆ t = S f - S i t f - t i

Como temos a função da posição e os instantes de tempo, podemos calcular esse deslocamento fácil fácil, né? Bora lá:

Para o tempo t=2 (final) temos:

x t = 5 t 3 - 8 t = 5.2 3 - 8.2 = 24 m

Para o tempo t=1 (inicial) temos:

x t = 5 t 3 - 8 t = 5.1 3 - 8.1 = - 3 m

E a diferença entre os instantes é: t f - t i = 2 - 1 = 1 s

Show!

Passo 2

Agora que temos a posição final e inicial e nosso delta t, podemos calcular a velocidade média!

v = ∆ S ∆ t   → v = S f - S i t f - t i

v = 24 - - 3 1 = 27 m / s

Conseguimos, show de bolinhas! E no enunciado, essa é a alternativa d.

Resposta

Alternativa d)

Exercício Resolvido #7

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 9º ed. Rio de Janeiro

A posição de um objeto que se move ao longo de um eixo x é dada por x   =   3 t   –   4 t ²   +   t ³ , onde x está em metros e t em segundos. Determine a posição do objeto para os seguintes valores de t :

(a) 1 s

(b) 2 s

(c) 3 s

(d) 4 s

(e) Qual o deslocamento do objeto entre t = 0 s e t = 4 s ?

(f) Qual é a velocidade média para o intervalo de tempo de t = 2 s a t = 4 s ?

(g) Desenhe o gráfico de x em função de t para 0   ≤   t   ≤   4 s e indique como a resposta do item (f) pode ser determinada a partir do gráfico.

Passo 1

Para resolver os item (a), (b), (c) e (d) é bem simples. Temos a equação que nos dá a posição do objeto em função do tempo. Basta substituir os tempos na equação. Fica da seguinte forma:

x = 3 t - 4 t 2 +   t 3

(a) Para t = 1 s :

x   =   ( 3 * 1 )   –   [ 4 * ( 1 ) ² ]   +   ( 1 ) ³

x   =   0   m

Passo 2

(b) Para t = 2 s :

x   =   ( 3 * 2 )   –   [ 4 * ( 2 ) ² ]   +   ( 2 ) ³

x   =   –   2   m

Passo 3

(c) Para t=3s:

x   =   ( 3 * 3 )   –   [ 4 * ( 3 ) ² ]   +   ( 3 ) ³

x   =   0   m .

Passo 4

(d) Para t = 4 s :

x   =   ( 3 * 4 )   –   [ 4 * ( 4 ) ² ]   +   ( 4 ) ³

  x   =   12   m

Passo 5

(e) Neste item iremos saber qual foi o deslocamento ( ∆ x ) do objeto no intervalo de entre 0 s e 4 s . Como sabemos, a variação ( ∆ ) é sempre: variável final – variável inicial.

Por analogia, a equação fornecida pelo exercício ficará da seguinte forma:

∆ x   =   3 ∆ t   –   4 ∆ t 2 +   ∆ t ³

∆ x é o que queremos calcular.

∆ t   =   t f i n a l     –   t i n i c i a l   =   4   –   0   =   4

Sendo assim,

∆ x   =   ( 3.4 )   –   [ ( 4 ) . ( 4 ) ² ]   +   ( 4 ) ³

∆ x   =   12   –   64   +   64  

∆ x   =   12   m

Passo 6

(f) Neste item iremos calcular a velocidade média para o intervalo de tempo de t = 2 s   a   t = 4 s .

Para problemas de velocidade média, a trajetória do objeto não importa! Apenas as posições inicial e final.

Da letra (b) tiramos a posição inicial do móvel ( t = 2 s ) que é de – 2 m .

Da letra (d) tiramos a posição final do móvel ( t = 4 s ) que é de 12 m .

∆ x   =   X f i n a l   –   X i n i c i a l   =   12   –   ( –   2 )   =   14 m

∆ t   =   t f i n a l   –   t i n i c i a l =   4   –   2   =   2 s

Assim,

      V m é d i a   =   ∆ x ∆ t   =   14 2   =   7 m / s .

Passo 7

(g) Neste item iremos esboçar o gráfico de x em função de   t no intervalo 0   ≤   t   ≤   4 s e indicar a resposta do item (f) no gráfico

Para esboçar o gráfico dessa questão, colocaremos os pontos no eixo cartesiano e vamos verificar como a função se comporta. Pontos já calculados ( t , x ):

(0,0)

(1,0)

(2,-2)

(3,0)

(4,12)

A reta tracejada que liga o ponto ( 2 , - 2 ) ao ( 4,12 ) está representando a velocidade média do objeto entre o intervalo t = 2 s e   t = 4 s .

Ufa , acabou rs Bora fazer mais exercícios e garintir a aprovação ??

Resposta

  1. x 1 = 0
  2. x 2 =   - 2 m
  3. x 3 = 0
  4. x 4 = 12 m
  5. x 4 - x 0 = 12 m
  6. v = 7 m / s

Exercício Resolvido #8

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 9º ed. Exercício Resolvido 8

A figura mostra uma situação na qual muitas pessoas tentam escapar por uma porta de emergência que está trancada. A pessoas se aproximam da porta com uma velocidade v s = 3,50 m / s , têm d = 0,25 m de espessura e estão separadas por uma distância L = 1,75 m. A figura abaixo mostra a posição das pessoas no instante t = 0.

a) Qual a taxa média de aumento da camada de pessoas que se comprimem contra a porta?

b) Em que instante a espessura da camada chega a D = 5,0 m?

Passo 1

Bora pra mais umaaaa!

Cara, o que você precisa perceber nessa questão não é nada mais nada menos que isso:

v m = ∆ s ∆ t

Se a pessoa se move uma distância   L com uma velocidade v s , temos que:

v s = L ∆ t

Então, o tempo que cada pessoa leva pra percorrer L com essa velocidade é

∆ t = L v s

E pelo enunciado da questão, a gente viu que com cada pessoa adicional, a profundidade da camada aumenta a profundidade de um corpo d sse liga só no esquema onde os bloquinhos coloridos são as pessoas.

Conforme as pessoas vão chegando na porta a camada D vai crescendo. Então, a taxa média de aumento é quanto aumenta essa distância D em um determinado tempo. Ou seja, é uma Velocidade Média também, né? :O

Essa é a sacada que cê tem que ter pra resolver essa questão! Então a taxa média vai ser calculada por:

T a x a = d ∆ t

Mas esse tempo aí é o mesmo tempo que a pessoa leva pra percorrer a distância L, que é o tempo de quando alguém anda essa distância e a taxa de pessoas aumenta! Haja coração nessa questão né, ufa.

Então temos:

T a x a = d ∆ t  

Substituindo ∆ t

T a x a = d L v s = d v s L

Substituindo os valores a gente vai ter:

T a x a = 0,25.3,50 1.75 = 0,5 m / s

Passo 2

Aqui ficou fácil, né? A gente já tem a velocidade da taxa de aumento e temos o valor de d. Só precisamos jogar na formulinha e descobrir o tempo!

T a x a = D ∆ t → ∆ t = D T a x a

∆ t = 5 0,5 = 10 s

Conseguimos!

Resposta

  1. 0,5 m / s
  2. 10 s

Exercícios de Livros Relacionados

Um vagonete de minério é puxado para o alto de uma encosta a 20k m / h e puxado ladeira abaixo a 35k m / h até a altura inicial. (O tempo gasto para inverter o movimento no alto da encosta é tão peque
A tartaruga começa a corrida 100m à frente de Aquiles. Este corre à velocidade de 10,0m / s , o dobro da velocidade da tartaruga. (A) Quanto tempo Aquiles leva para alcançar a tartaruga? (B) Quanto te
Refaça o exercício 2.1 para o caso (proposto por Zenão) em que Aquiles faz 10m / s e a tartaruga 1m / s .
Considere o caso mais geral do problema de Zenão. As velocidades de Aquiles e da tartaruga são respectivamente, v A e v t e a corrida começa com a tartaruga à distância d à frente de Aquiles. Quanto t
Tomando movimento orbital da Lua em torno da Terra como circular uniforme de raio 3,82 × 10 8m e período de 27,3 dias, calcule a aceleração centrípeta da Lua.