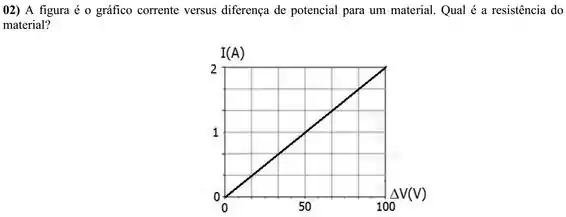
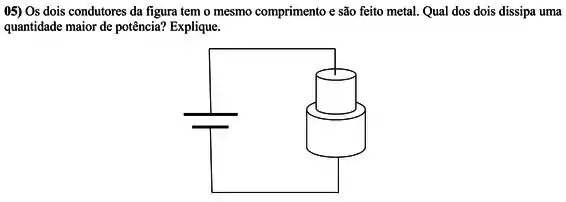
Exercícios de Resistência e Resistividade - Lista de Exercícios Resolvida
Questão 1
Quando são aplicados entre as extremidades de um fio que possui de comprimento e de raio, a densidade de corrente é igual a .
Determine a resistividade do fio.
Ver solução completaQuestão 2
Uma barra de cobre cilíndrica, de resistência elétrica , comprimento e seção reta , é comprimida para a metade do seu comprimento original, sem que seu volume se altere.
Pode-se afirmar que o novo valor de sua resistência elétrica é:
Ver solução completa
Questão 3
Os enrolamentos de cobre de um motor têm uma resistência de a quando o motor está frio. Depois de o motor trabalhar durante várias horas, a resistência aumenta para .
Qual é a nova temperatura dos enrolamentos? Suponha que as dimensões dos enrolamentos não variem.
Dado: .
Ver solução completaQuestão 4
As especificações de uma lâmpada de lanterna são e (os valores da corrente e tensão de trabalho, respectivamente).
Se a resistência do filamento de tungstênio da lâmpada à temperatura ambiente é , qual é a temperatura do filamento quando a lâmpada está acesa?
Dado: .
Ver solução completaQuestão 5
Três resistores cilíndricos circulares ôhmicos, 1, 2 e 3, são construídos com o mesmo material, de resistividade conhecida . O resistor 1 tem comprimento e área de seção reta , o resistor 2 tem comprimento e área de seção reta , enquanto o resistor 3 tem comprimento e área de seção reta .
Se cada um desses resistores for submetido a uma mesma diferença de potencial entre suas extremidades, podemos afirmar, sobre os módulos das densidades de corrente que fluem ao longo deles, que
.
.
.
.
.
Ver solução completaQuestão 6
A figura é o gráfico corrente versus diferença de potencial para um material. Qual é a resistência do material?
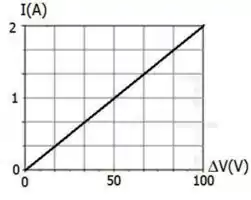
Questão 7
Um fio de Nichrome (uma liga de níquel, cromo e ferro muito usada em elementos de aquecimento) tem de comprimento e de seção reta e conduz uma corrente de quando uma diferença de potencial de é aplicada a suas extremidades.
Calcule a condutividade do Nichrome.
Ver solução completaQuestão 8
Uma barra de cobre cilíndrica, de resistência elétrica , comprimento e seção reta , é comprimida para a metade do seu comprimento original, sem que seu volume se altere.
Pode-se afirmar que o novo valor de sua resistência elétrica é:
Ver solução completa
Questão 9
Três resistores cilíndricos circulares ôhmicos, 1, 2 e 3, são construídos com o mesmo material, de resistividade conhecida . O resistor 1 tem comprimento e área de seção reta , o resistor 2 tem comprimento e área de seção reta , enquanto o resistor 3 tem comprimento e área de seção reta .
Se cada um desses resistores for submetido a uma mesma diferença de potencial entre suas extremidades, podemos afirmar, sobre os módulos das densidades de corrente que fluem ao longo deles, que
.
.
.
.
.
Ver solução completaQuestão 10
Considere duas cascas cilíndricas condutoras coaxiais sendo que a casca interior possui raio e a exterior, raio . As cascas cilíndricas possuem comprimento . O espaço entre as cascas é preenchido uniformemente com um material cuja resistividade é . Entre os duas cascas é aplicada uma diferença de potencial tal que a corrente medida no dispositivo é .
As respostas dos itens abaixo deverão ser dadas em função apenas dos dados do problema que são , , , , e .
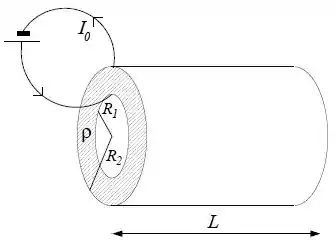
Calcule o vetor densidade de corrente a uma distância do eixo dos cilindros.
Determine o vetor campo elétrico entre os cilindros.
Usando o campo elétrico obtido em , calcule a diferença de potencial entre os cilindros.
Calcule a resistência do sistema.
Ver solução completaQuestão 11
A região entre duas cascas esféricas condutoras concêntricas de raios e com é preenchida com um material de resistividade elétrica , onde é a distância até o centro das cascas esféricas e é uma constante.
Ligando-se uma bateria às cascas esféricas como na figura observa-se uma corrente no sentido indicado.
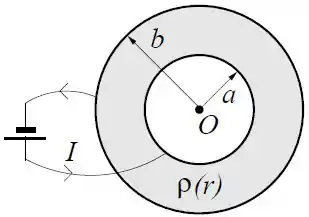
- Calcule o vetor densidade de corrente na região entre as cascas .
- Usando a lei de Ohm, determine o vetor campo elétrico entre as cascas esféricas.
- Calcule a resistência desse sistema em função de , e .
Questão 12
Uma casca cilíndrica é feita de um material condutor de condutividade uniforme. As dimensões do cilindro estão indicadas na figura, onde . As superfícies interna e externa da casca com raios e , onde é a distância até o eixo da casca cilíndrica, são duas equipotenciais mantidas a uma ddp igual a por uma bateria, conforme a figura.
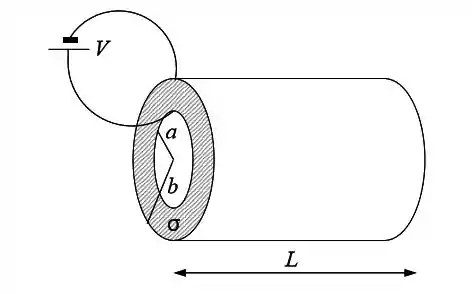
(a) Devido à simetria, a densidade de corrente é dada por . Calcule como função de , suposta conhecida.
(b) Calcule o vetor no interior da casca como função de .
(c) Calcule a resistência da casca.
(d) Calcule o ponto em função de e .
Ver solução completaQuestão 13
Dos fios (1 e 2) condutores, cilíndricos circulares, homogêneos, de mesmo comprimento e área de seção reta, são unidos em série. A resistividade elétrica do fio 1 é o dobro da do fio 2. Existe uma diferença de potencial entre as extremidades do fio combinado. Quais são as razões e entre os módulos das densidades de corrente (estacionárias) e dos campos elétricos nos fios 1 e 2, respectivamente?
a)
b)
c)
d)
e)
Ver solução completaQuestão 14
Em um experimento de laboratório uma aluna constrói um cilindro de massa condutora de raio e comprimento . A seguir ela constrói outro cilindro com o mesmo material do primeiro, porém de raio e comprimento . A relação entre a resistência do primeiro cilindro (de raio ) e a resistência do segundo cilindro (de raio ) é igual a:
Ver solução completa
Questão 15


(A) A intensidade de campo elétrico no fio é menor que no fio
(B) A intensidade de campo elétrico no fio é maior que no fio
(C) As intensidades de campo elétrico são iguais.
(D) As intensidades de campo elétrico em ambos os segmentos são iguais a zero
(E) Com essa informação fornecida não é possível comparar as intensidades de campo elétrico e nos segmentos.
Ver solução completaQuestão 16
A figura abaixo é o gráfico da corrente versus diferença de potencial para um material.
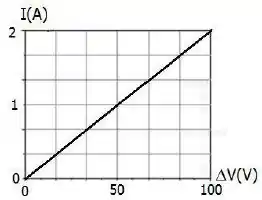
Qual é a resistência do material?
Ver solução completa
Questão 18
Quanto vale a resistência, em , de um fio cilíndrico condutor de alumínio de resistividade , de comprimento e de diâmetro? Obs: utilize uma casa decimal no seu resultado.
Ver solução completaQuestão 19
Um fio de cobre (de resistividade ) é usado para formar um anel de raio igual a . A área da seção reta do fio é de .
Os pontos e estão angularmente separados de , como mostra a figura.
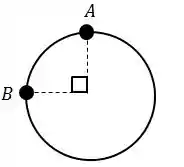
A resistência entre os pontos e é, aproximadamente:
;
;
;
;
Ver solução completaQuestão 20
Nove fios idênticos, cada um com diâmetro e comprimento , são conectados em série. Esta combinação tem a mesma resistência de um único fio de comprimento , mas com diâmetro de:
(a)
(b) .
(c)
(d)
(e)
Ver solução completaQuestão 21
Quando uma diferença de potencial de é aplicada às extremidades de um fio de de comprimento com raio de , o módulo da densidade de corrente . Determine a resistividade do fio.
(a) .
(b)
(c)
(d)
(e)
Ver solução completaQuestão 22
6ª questão - Um resistor, feito de um fio longo de comprimento , é conectado aos terminais de uma bateria que fornece uma tensão elétrica constante . Nesta situação, uma corrente elétrica flui através do resistor. Em seguida, o resistor é cortado ao meio, em dois segmentos de comprimento . Os dois resistores são então conectados em paralelo aos terminais da mesma bateria. Qual a potência fornecida pela bateria nesta nova situação?
A)
B)
C)
D)
E)
Ver solução completaQuestão 23
Um resistor cilíndrico de comprimento deveria ter uma seção reta ao longo de todo seu comprimento e uma resistência igual a . Devido a um erro de fabricação, metade do resistor apresenta uma seção reta , conforme a figura.
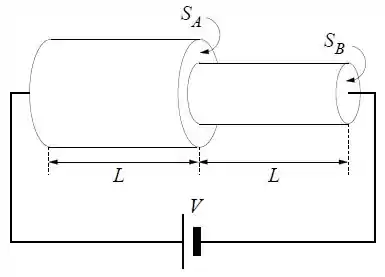
Determine a resistência do resistor em termos do valor projetado .
Aplica-se uma ddp de volts nas extremidades do resistor. Calcule os módulos dos campos elétricos e em cada um dos trechos do resistor em termos de e .
Ver solução completaQuestão 24
Um material condutor de condutividade uniforme tem o formato de um semi-círculo de altura e raios e , conforme indicado nas figuras e , respectivamente. As superfícies localizadas em e são equipotenciais e mantidas a uma diferença de potencial por uma bateria. Vamos assumir que o potencial elétrico dentro do condutor depende somente da coordenada , de forma que os efeitos de borda podem ser desprezados.
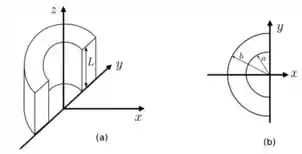
- A bateria fornece uma corrente elétrica . Assumindo a conservação de corrente, determine o vetor densidade de corrente .
- Determine o campo elétrico no interior do condutor.
- Calcule a resistência do condutor em função de sua condutividade e de suas dimensões.
Questão 25
Considere as seguintes afirmações sobre condução elétrica num condutor homogêneo e isotrópico:
- Energia potencial elétrica é transformada em calor ao conectar-se o condutor aos terminais de uma bateria
- A resistividade elétrica e uma propriedade intensiva da substância que compõe o condutor, isto é, não depende da geometria do condutor.
- A resistência de um condutor depende da sua geometria
Das afirmativas mencionadas:
- Apenas a i é falsa
- Apenas a ii é falsa
- São todas corretas
- Apenas i e ii são falsas
- Apenas a iii é falsa
Questão 26
Considere o circuito com resistores abaixo
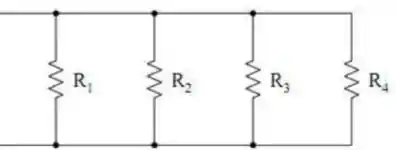
Se o valor de cada resistor for de 6 ohms, a resistência equivalente total será de:
Ver solução completaQuestão 27
Considere um fio de de diâmetro e de comprimento . Se uma diferença de potencial de é aplicada a este fio, a corrente que o atravessa é . De acordo com os valores de resistividade () dado nas alternativas abaixo, de que material é feito o fio?
Alumínio ( )
Cobre ()
Ouro ()
Ferro ()
Prata ()
Ver solução completaQuestão 28
Um fio condutor retilíneo de comprimento tem a seção transversal mostrada na figura abaixo. Ele é formado por um cilindro condutor de raio e resistividade cercado por uma casca condutora cilíndrica de raio interno , raio externo e resistividade . Se uma corrente flui paralelamente ao eixo deste fio e o campo elétrico é constante em seu interior, podemos afirmar que a resistência elétrica deste fio vale:
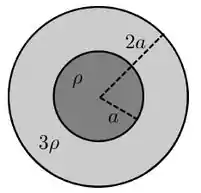
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 29
Um fio cilíndrico está ao longo do eixo , tem comprimento , diâmetro e resistividade , sendo este material um condutor ôhmico. Considere que o potencial é e .
Em termos de e constantes físicas, deduza expressões para:
O campo elétrico no fio;
A resistência elétrica no fio;
A corrente no fio;
A densidade de corrente;
Qual é a expressão do campo elétrico em função de e ?
Ver solução completaQuestão 31
(Cap 26 Ex – 32) A atmosfera inferior da Terra contém íons negativos e positivos que são produzidos por elementos radioativos do solo e por raios cósmicos provenientes do espaço. Em uma certa região, a intensidade do campo elétrico atmosférico é e o campo é dirigido verticalmente para baixo. E e campo faz com que íons com uma unidade de carga positiva e uma densidade de se movam para baixo, enquanto íons com uma unidade de carga negativa e uma densidade de se movam para cima (Fig26-27). O valor experimental da condutividade do ar nessa região é . Determine (a) o módulo da densidade de corrente e (b) a velocidade de deriva dos íons, supondo que é a mesma para íons positivos e negativos.
Ver solução completaQuestão 32
Considere um fio condutor, ôhmico, cilíndrico, circular, fino constituído por duas partes: a primeira metade com seção reta de área , comprimento e resistividade elétrica e a segunda metade com seção reta da mesma área , comprimento e resistividade .
Supondo que uma corrente estacionária percorre tal fio, qual é a relação entre os módulos dos campos elétricos no interior de cada uma de suas metades?
.
.
.
.
.
Ver solução completaQuestão 33
06) Um condutor cilíndrico de raio , comprimento e resistividade tem uma resistência . Este condutor é derretido e transformado num novo condutor, também cilíndrico, com de seu comprimento original. A resistência do novo condutor é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 34
Nos materiais condutores ôhmicos há uma relação linear entre a corrente elétrica e a diferença de potencial. Verdadeiro ou falso?
Ver solução completaQuestão 35
A figura ao lado representa as medidas de tensão elétrica versus corrente para um fio condutor de de comprimento e diâmetro . A resistividade elétrica do condutor é:
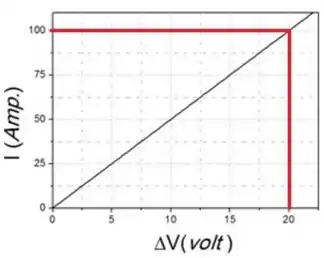
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 36
Dois resistores cilíndricos são feitos do mesmo material (mesma resistividade). O resistor 2 tem o dobro do comprimento e o dobro do diâmetro do resistor 1. Qual é a razão enre suas resistências?
- ;
- ;
- ;
- ;
- .
Questão 37
Considere dois fios condutores ôhmicos, retilíneos e feitos do mesmo material. O primeiro possui um comprimento e área de seção transversal igual a , enquanto o segundo possui comprimento e área de seção transversal igual a . Seja a resistência elétrica do primeiro fio e a do segundo. Nessa situação, a razão vale:
Questão 38
(Cap 26 Ex – 27) Dois condutores são feitos do mesmo material e têm o mesmo comprimento. O condutor A é um fio maciço de de diâmetro; o condutor B é um tubo oco com um diâmetro externo de e um diâmetro interno de . Qual é a razão entre as resistências dos dois fios, ? As resistências são medidas entre as extremidades dos fios.
Ver solução completaQuestão 39
(Cap 26 Ex – 15) Uma bobina é formada por 250 espiras de fio isolado de cobre calibre 16 (diâmetro: ) enroladas em uma única camada em uma forma cilíndrica de de raio. Qual é a resistência da bobina? Despreze a espessura do isolamento. (Sugestão: use a Tabela 26-l.)
Ver solução completaQuestão 40
Considere dois fios condutores cilíndricos A e B de mesmo comprimento, feitos de um mesmo material e com diâmetros distintos. Para comparar as espessuras dos dois fios, mediu-se a corrente que atravessa cada fio como função da diferença de potencial à qual está submetido. Os resultados estão representados na figura. Analisando os resultados, conclui-se que a relação entre os diâmetros dos fios A e B é:
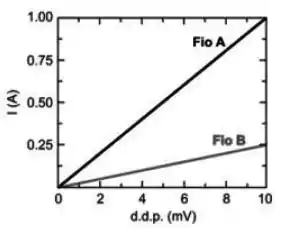
Questão 41
Três resistores cilíndricos circulares ôhmicos, , e , são construídos com o mesmo material, de resistividade conhecida . O resistor tem comprimento e área de seção reta , o resistor tem comprimento e área de seção reta , enquanto o resistor tem comprimento e área de seção reta . Se cada um desses resistores for submetido a uma mesma diferença de potencial entre suas extremidades, podemos afirmar, sobre os módulos () das densidades de corrente que fluem ao longo deles e sobre suas resistências que:
- e
- e
- e
- e
- e
Questão 42
(Cap 26 Ex – 23) Quando uma diferença de potencial de é aplicada às extremidades de um fio de de comprimento com um raio de , o módulo da densidade de corrente é . Determine a resistividade do fio.
Ver solução completaQuestão 43
(Cap 26 Ex – 29) Uma diferença de potencial de é estabelecida entre as extremidades de um fio de cobre de de comprimento com um raio de . Qual é a carga que passa por uma seção reta do fio em 3,00 ms?
Ver solução completaQuestão 44
O filamento de uma lâmpada incandescente, submetido a uma tensão , é percorrido por uma corrente de intensidade . O gráfico abaixo mostra a relação entre e .
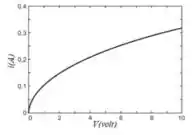 As seguintes afirmações se referem a essa lâmpada.
As seguintes afirmações se referem a essa lâmpada.
- A resistência do filamento é a mesma para qualquer valor da tensão aplicada.
- A resistência do filamento diminui com o aumento da corrente.
- A potência dissipada no filamento aumenta com o aumento da tensão aplicada.
Dentre essas afirmações, somente
- I está correta.
- II está correta.
- III está correta.
- I e III estão corretas
- II e III estão corretas.
Questão 46
Os condutores 1 e 2 da figura abaixo são confeccionados de materiais diferentes. Os dois condutores têm comprimentos e , respectivamente. A resistividade e o diâmetro do condutor 1 são, respectivamente, e . A resistividade e o diâmetro do condutor 2 são e , respectivamente. Os dois condutores são unidos na forma mostrada na figura e são submetidos a uma corrente . Determine:
- A resistência de cada um dos condutores.
- A diferença de potencial entre as extremidades dos condutores (pontos e da figura abaixo).
- A potência total dissipada por ambos os dois condutores.
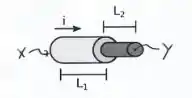
Questão 47
(Cap 26 Ex – 34) A Fig. 26-28 mostra um fio 1, com de diâmetro, e um fio 2, com de diâmetro, ligados por um trecho de fio em que o diâmetro varia gradualmente. O fio é de cobre e está sendo percorrido por uma corrente distribuída uniformemente ao longo de qualquer seção reta do fio . A variação do potencial elétrico V ao longo do comprimento do fio 2 é . O número de portadores de carga por unidade de volume é . Qual é a velocidade de deriva dos elétrons de condução no fio l ?
Ver solução completaQuestão 48
Um bastão cilíndrico de cobre de comprimento e raio é conectado a outro bastão, também de cobre, de comprimento e raio , formando um objeto de comprimento , conforme a figura.
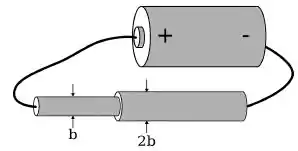
O objeto é conectado a uma bateria de forma a se estabelecer uma corrente através dele. Como se relacionam as magnitudes dos campos elétricos dentro do fio de raio e ?
Ver solução completa
Questão 49
A corrente elétrica como função da voltagem em um resistor é representada pelo gráfico abaixo.
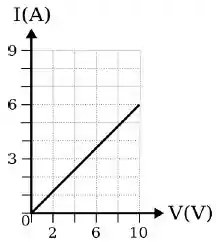
Qual é o valor aproximado da resistência do resistor?
Ver solução completa
Questão 50
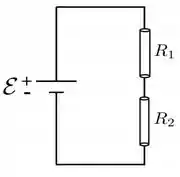
2 - Os resistores Ôhmicos 1 e 2 (com ) são conectados em série, através de fios ideais, a uma bateria de fem . Sabe-se que os resistores apresentam geometria cilíndrica com mesmos comprimento e área de seção reta: e . Sendo e as conduvidades dos materiais, e os campos elétricos no interior dos resistores, e as densidades de corrente nos resistores, é CORRETO afirmar que:
Questão 51
5 - Uma densidade de corrente uniforme circula através de um fio de comprimento quando conectado aos terminais de uma pequena bateria ideal com fem . Qual a resistividade ⍴ do material do fio?
Questão 52
8 - A lei de Ohm nos diz que:
- Quanto maior a resistividade de um material, maior será a resposta da densidade de corrente para um campo elétrico fixo.
- Quanto menor a resistividade de um material, maior a densidade de corrente para um campo elétrico fixo.
- Quanto menor a condutividade de um material, maior a densidade de corrente para um campo elétrico fixo.
- Quanto menor a resistividade de um material, menor a densidade de corrente para um campo elétrico fixo.
- Quanto maior a condutividade de um material, menor a densidade de corrente para um campo elétrico fixo.
Questão 53
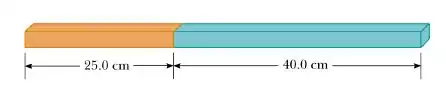
A barra na figura abaixo é formada por dois materiais diferentes. Ambos possuem uma seção transversal quadrada de lado igual a . O primeiro material possui uma resistividade e comprimento , enquanto o segundo tem resistividade e comprimento . Qual dos valores abaixo melhor representa a resistência elétrica dessa barra entre as suas extremidades?
Questão 54
Dois fios condutores cilíndricos, e de mesmo comprimento e mesmo material são ligados à mesma diferença de potencial. O condutor tem o dobro do raio do condutor . Qual é a razão entre as potências dissipadas nos condutores e ?
a)
b)
c)
d)
e)
Ver solução completaQuestão 55
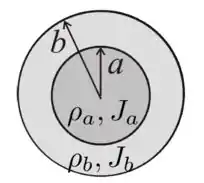
Um fio condutor retilíneo é constituído por um cilindro condutor de raio e resistividade e uma casca cilíndrica condutora maciça de raio interno , raio externo () e resistividade , coaxial ao cilindro. Uma seção transversal deste é mostrada na figura abaixo. Sabendo que o fio é submetido a uma diferença de potencial constante entre suas extremidades, a razão entre as intensidades das densidades de corrente que fluem no cilindro e na casca cilíndrica vale:
Questão 56
Um fio condutor cilíndrico tem comprimento e resistência elétrica . Tal fio é esticado de tal forma que seu comprimento passa a ser . Sabe-se que o volume do cilindro, antes e depois do processo de estiramento, mantém-se constante. Qual é a resistência elétrica do fio, depois dele ter sido esticado para o comprimento ?
(a).
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 57
Com a associação de três resistores, de mesma resistência , é possível obter-se um certo número de resistências equivalentes, distintas entre si. Dentre as associações possíveis, o máximo valor da resistência equivalente é, em ohms:
Questão 58
Para um condutor ôhmico, a resistividade é a constante de proporcionalidade entre:
a corrente e a diferença de potencial;
a corrente e o campo elétrico;
a densidade de corrente e o campo elétrico;
a densidade de corrente e a diferença de potencial;
a diferença de potencial e o campo elétrico.
Ver solução completa