Exercícios de Energia Cinética de Rotação - Lista de Exercícios Resolvida
Questão 1
Na Fig. 10-36, duas partículas ambas de massa , estão ligadas uma à outra e a um eixo de rotação em por duas barras finas, ambas de comprimento e massa . O conjunto gira em torno do eixo de rotação com velocidade angular . Em relação a , quais são (a) o momento de inércia do conjunto e (b) a energia cinética do conjunto?
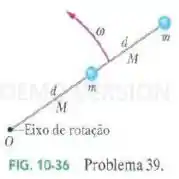
Questão 2
Um poste cilindrico, fino e homogêneo de 10 metros de altura é derrubado, a partir da posição vertical. Sua base permanece fixa durante sua queda. Qual a velocidade da ponta do poste quando ele atinge o chão?(Despreze os atritos e dissipações neste caso.)
a)
b)
c)
d)
e)
Dados:
Momento de inércia de uma barra:
Ver solução completaQuestão 3
Calcule o momento de inércia de uma roda que tem uma energia cinética de quando gira a .
Ver solução completaQuestão 4
Um carro tem uma roda de massa e raio com momento de inércia relativo ao seu eixo de rotação que passa pelo seu centro de massa. O carro arranca em movimento retilíneo com a roda patinando na pista de modo que a velocidade de seu centrode massa esteja relacionada com sua velocidade angular de rotação por meio de . Nesse caso, a energia cinética da roda é
- ;
- ;
- ;
- ;
- ;
Questão 5
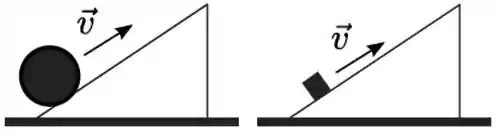
Uma esfera é lançada rolando sem deslizar subindo um plano inclinado com velocidade inicial do seu centro de massa. Um bloco é lançado subindo em translação um plano inclinado com a mesma inclinação e com a mesma velocidade inicial do seu centro de massa. No plano onde se encontra a esfera há atrito suficiente para que ela permaneça rolando sem deslizar e no plano onde está o bloco não há atrito.
A relação entre a altura máxima que o bloco atinge e a altura máxima que a esfera atinge nos respectivos planos é dada por
(a) , pois tanto a energia cinética do bloco como a da esfera se conserva.
(b) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
(c) , pois o bloco desliza sem atrito.
(d) , pois a esfera rola sem deslizar.
(e) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
Ver solução completaQuestão 6
Um carro tem uma roda de massa e raio com momento de inércia relativo ao seu eixo de rotação que passa pelo seu centro de massa. O carro arranca em movimento retilíneo com a roda patinando na pista de modo que a velocidade de seu centro de massa esteja relacionada com sua velocidade angular de rotação por meio de . Nesse caso, a energia cinética da roda é
- ;
- ;
- ;
- ;
- ;
Questão 7
(Cap 10 – Ex 67) Uma chaminé cilíndrica cai quando a base sofre um abalo. Trate a chaminé como uma barra fina com de comprimento. No instante em que a chaminé faz um ângulo de com a vertical durante a queda, qual é
a) a aceleração radial do topo e
b) a aceleração tangencial do topo? (Sugestão: use considerações de energia e não de torque.)
c) Para que ângulo a aceleração tangencial é igual a ?
Ver solução completaQuestão 8
(Cap 11 – Ex 5) Um aro de rola em um piso horizontal de tal forma que o centro de massa tem uma velocidade de . Qual é o trabalho necessário para fazê-lo parar?
Ver solução completaQuestão 9
Três partículas de massas , e diferentes movem-se com a mesma velocidade vetorial constante relativas a um dado referencial. Sendo a energia cinética do sistema e a energia cinética do seu centro de massa, relativas a esse referencial inercial, e sua energia cinética relativa ao centro de massa, é correto afirmar que:
- com e ambas diferentes de zero;
- com e ambas diferentes de zero;
- é sempre nula;
- ;
Questão 10
Um disco homogêneo de raio e massa rola sem deslizar sobre uma superfície horizontal com velocidade angular constante. O momento de inércia deste disco em relação ao eixo que passa pelo seu centro de massa, perpendicularmente ao disco, é igual a . A energia cinética desse disco é
- ;
- ;
- ;
- ;
- ;
Questão 11
Uma esfera de raio e massa rola sem deslizar sobre uma mesa horizontal com velocidade angular constante. Sabendo-se que o momento de inércia de uma esfera segundo um eixo que passa pelo seu centro é , a energia cinética desta esfera é:
Questão 12
(Cap 11 – Ex 8) Na Fig. 11-32, uma bola maciça de latão de massa rola suavemente ao longo do trilho quando é liberada a partir do repouso no trecho retilíneo. A parte circular do trilho tem um raio e a bola tem um raio .
a) Quanto vale se a bola está na iminência de perder contato com o trilho quando chegar ao ponto mais alto da parte curva do trilho?
Se a bola é liberada a uma altura , quais são
b) o módulo e
c) a orientação da componente horizontal da força que age sobre a bola no ponto ?
Ver solução completaQuestão 13
Uma roldana maciça e homogênea tem seu eixo central fixo e pode ser solicitada a girar por cordas presas tanto a seu raio interno , quanto a seu raio externo . A roldana sustenta por seu raio interno um corpo de massa , e está atrelada, por seu raio externo, a uma mola de constante elástica . O sistema está inicialmente em repouso com a mola destendida de .
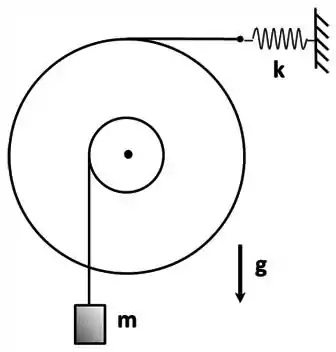
) O sistema é liberado e num determinado instante a distensão da mola vale de . Calcule a variação da altura do corpo desde que o sistema foi liberado até este instante, respondendo se o corpo subiu ou desceu.
) Calcule a velocidade angular da roldanano instante considerado no item . Considere que a variação de altura do corpo é de , que o momento de inércia da roldana vale e
Ver solução completaQuestão 14
Um sistema composto por uma haste delgada de massa e comprimento e um aro fino de raio desconhecido e mesma massa é livre para girar em torno do eixo . Determine, fornecendo as respostas com o número de algarismos significativos adequado:
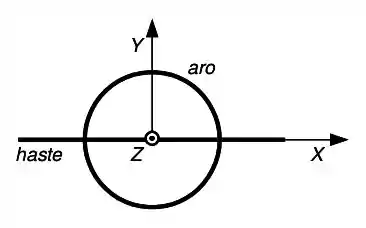
a) O valor de que faz o momento de inércia do aro ser igual ao momento de inércia da haste.
b) Determine a aceleração angular necessária para levar o sistema do repouso até que um ponto na extremidade da haste possua velocidade tangencial em
c) Suponha agora que o momento de inércia do conjunto seja e que ele gire com velocidade angular . Determine o trabalho necessário para levar o sistema ao repouso completo
d) Se o eixo de rotação for movido paralelamente até a extremidade da haste qual o novo momento de inércia do conjunto neste novo eixo?
Dados:
Ver solução completaQuestão 15
Uma haste rígida vertical de massa e comprimento pode girar livremente em torno do eixo horizontal (perpendicular ao papel) que passa por sua extremidade inferior. O momento de inércia da haste em relação ao eixo de rotação é . A haste é liberada a partir do repouso e começa a girar em torno de sua extremidade inferior. Quando passa pela posição vertical invertida, o módulo da velocidade angular da haste é

(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 16
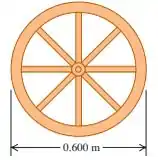
Uma roda de carroça é feita como indicado na figura abaixo. O raio da roda é igual a e possui massa igual a . Cada um dos seus oito aros, distribuídos ao longo de diâmetros, possuem comprimento de e massa igual a . Qual é o momento de inércia da roda em relação a um eixo perpendicular ao plano da roda e passando pelo seu centro?
Questão 17
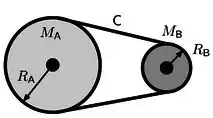
Duas polias com massas e estão acopladas através de uma correia de massa desprezível, como mostra a figura ao lado. A polia é acelerada a partir do repouso com aceleração angular durante o tempo .
As polias têm raios e , respectivamente, e podem girar sem atrito.
O momento de inércia de uma polia é dado por .
- Calcule as velocidades angulares das polias e no instante de tempo
- Obtenha a fração entre as energias cinéticas das polias e , no instante de tempo .
Questão 18
Um alvo é constituído por uma placa quadrada de madeira vertical com lado igual a e massa de , pivotada em um eixo horizontal situado em seu topo. A placa é atingida frontalmente em seu centro por uma bala de massa igual a que se desloca a e que fica retida no interior da placa.
a) Qual é a velocidade angular da placa logo após o impacto da bala?
Ver solução completaQuestão 19
Uma roda com momento de inércia é fixada no seu eixo de simetria e está livre para girar sem atrito. A velocidade angular da roda é aumentada de zero até em um intervalo de tempo . Qual é a potência média da roda durante este intervalo de tempo?
Ver solução completaQuestão 20
Um poste cilindrico, fino e homogêneo de 10 metros de altura é derrubado, a partir da posição vertical. Sua base permanece fixa durante sua queda. Qual a velocidade da ponta do poste quando ele atinge o chão?(Despreze os atritos e dissipações neste caso.)
a)
b)
c)
d)
e)
Questão 21
Para um disco de massa e raio , que rola sem deslizar, o que é maior, sua energia cinética translacional ou sua energia cinética de rotação em relação ao centro de massa?

Questão 22
Uma esfera sólida homogênea, de massa e raio , gira com velocidade angular em torno de um eixo que passa pelo seu centro. Um cilindro sólido homogêneo, de massa e raio , gira em torno do seu eixo central, paralelo ao comprimento do cilindro. Responder justificando:
Qual deve ser a velocidade angular do cilindro para que ele tenha a mesma energia cinética rotacional que a esfera?
Ver solução completaQuestão 23
Uma barra fina e homogênea de massa e comprimento é liberada na posição horizontal a partir do repouso e gira em torno de um eixo horizontal fixo, perpendicular a ela e que passa por uma de suas extremidades. Sabendo que não há atrito entre a barra e o eixo e que o momento de inércia da barra relativo ao eixo é igual a , podemos afirmar que ao passar pela posição vertical a velocidade do centro de massa da barra é
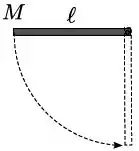
- ;
- ;
- ;
- ;
- ;
Questão 24
(Capítulo 9.1 – Exercício 30) Uma mesa giratória, girando a , é levada ao repouso em 26 s. Supondo constante a aceleração angular, encontre (a) a aceleração angular. Durante esses , determine (b) a rapidez angular média e (c) o deslocamento angular em número de voltas.
Ver solução completaQuestão 25
A figura mostra três discos homogêneos e feitos do mesmo material em rotação em torno de seus eixos de simetria. O ordenamento correto das energias rotacionais dos discos é:
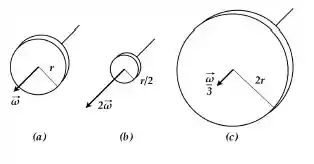
Dados: (cilindro)
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 26
[ENUNCIADO COMUM ÀS QUESTÕES 5 E 6]
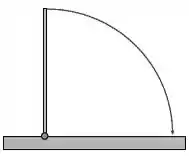
Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Considere e que o momento de inércia de uma barra de massa e comprimento em torno de um eixo que passa pelo seu centro de massa é .
[QUESTÃO 6]
Qual é a energia cinética da barra quando ela faz um ângulo com a horizontal?
(a) J
(b) J
(c) J
(d) J
(e) J
(f) J
(g) J
(h) J
(i) J
Ver solução completaQuestão 27
Uma bengala delgada de comprimento é constituída de uma haste homogênea de massa e uma pequena esfera de massa de raio desprezível na extremidade. Inicialmente equilibrada na vertical, ela começa a tombar mantendo o ponto de contato com o solo fixo devido ao atrito estático. Considerando a rotação em torno do eixo perpendicular à figura que passa pelo ponto de contato entre a bengala e o solo, determine a velocidade angular da esfera imediatamente antes de colidir com o solo.
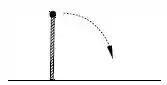
a)
b)
c)
d)
e)
Ver solução completaQuestão 28
Dois blocos de massas e estão ligados por um fio ideal que passa por uma roldana homogênea, também de massa , e de raio . A roldana é sustentada por um eixo horizontal coincidente com seu eixo geométrico de simetria, como ilustra a figura. Não há atrito entre o eixo e a roldana e o fio não desliza sobre ela. Considere o intervalo de tempo com um instante inicial em que a roldana e os blocos estão em repouso e um instante final em que o bloco mais pesado já desceu uma distância vertical .
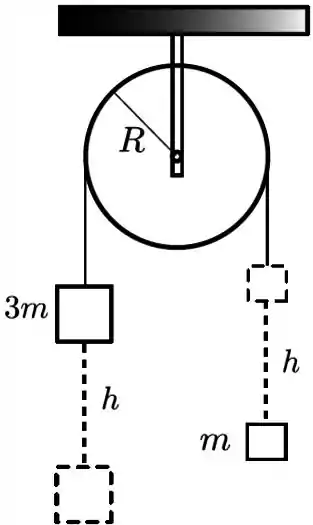
Considere como dados e o módulo da aceleração da gravidade. O momento de inércia da roldana relativo ao seu eixo de simetria é . Calcule
a) a variação da energia cinética do sistema constituído pela roldana e os blocos no intervalo de tempo considerado;
b) o módulo da velocidade do bloco mais pesado no instante final;
c) a razão entre a energia cinética de rotação da roldana e a energia cinética total de translação dos dois blocos no instante final.
Ver solução completaQuestão 29
Uma roldana maciça e homogênea tem seu eixo central fixo e pode ser solicitada a girar por cordas presas tanto a seu raio interno , quanto a seu raio externo . A peça toda é rígida.
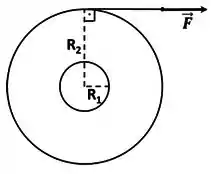
Uma força de módulo constante igual a e direção sempre perpendicular ao raio externo da roldana a acelera desde o repouso até o instante em que sua velocidade angular vale . Durante essa rotaçãoo, o deslocamento angular da roldana é de 3,2 rad. Usando que , calcule o momento de inércia da roldana.
Calcule a potencia instantenea desenvolvida pela força no instante considerado no item .
Ver solução completaQuestão 30
Qual é a energia cinética de rotação do sistema de partículas da questão 17 se ele gira a 2,0 rev/s em torno de um eixo perpendicular ao plano e que passa pelo ponto O da figura acima ?
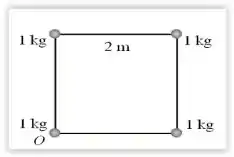
(A) 1,3 x J
(B) 7,9 x J
(C) 0
(D) 0,32 x J
(E) 0,50 x J
Ver solução completaQuestão 31
Um disco e um anel de mesmo raio, mesma massa total e mesma velocidade, rolam sem deslizar sobre uma superfície plana. Em um dado momento, ambos encontram um plano inclinado e o sobem até pararem momentaneamente. Qual a razão entre a altura máxima atingida pelo anel pela altura máxima atingida pelo disco? Formulário: ,
A.
B.
C.
D.
E.
Ver solução completaQuestão 32
(Cap 9 – Ex 34) Qual é a rapidez angular da Terra, em radianos por segundo, na rotação em torno de seu eixo?
Ver solução completaQuestão 33
(Cap 9 – Ex 32) Uma roda-gigante de de raio completa uma volta a cada . (a) Qual é a sua rapidez angular (em radianos por segundo)? (b) Qual é a rapidez linear de um passageiro? (c) Qual é a aceleração de um passageiro?
Ver solução completaQuestão 34
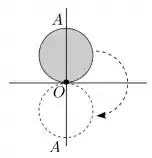
Um disco de raio R e de massa M uniformemente distribuída, possui um pequeno furo na sua periferia. Por este furo o disco é colocado no pino O, preso a uma parede vertical. No posicionamento inicial do disco o ponto A de sua periferia localizado diametralmente oposto a O está sobre o eixo vertical, acima de O; conforme mostra a figura abaixo. Como o disco está sob a condição de equilíbrio instável, ele cai girando em torno do pino O. Sabe-se que o momento de inércia deste disco em torno de um eixo que passa pelo centro de massa e perpendicular e ele é igual . Desprezando-se o atrito entre o pino e o disco, quando o ponto A passa pela linha vertical, abaixo de O, a velocidade angular ω do disco, é igual a:
Questão 35
(Capítulo 9.1 – Exercício 33) Um ciclista acelera uniformemente a partir do repouso. Após , as rodas completam . (a) Qual é a aceleração angular das rodas? (b) Qual é a rapidez angular das rodas ao final dos ?
Ver solução completaQuestão 36
(Capítulo 9.1 – Exercício 31) Um disco de 12 cm de raio, que começa a girar em torno de seu eixo em , gira com uma aceleração angular constante de . Em , (a) qual é a rapidez angular do disco e (b) quais são as componentes tangencial e centrípeta da aceleração de um ponto na borda do disco?
Ver solução completaQuestão 37
(Cap 9 – Ex 34) Qual é a rapidez angular da Terra, em radianos por segundo, na rotação em torno de seu eixo?
Ver solução completaQuestão 38
(Capítulo 9.1 – Exercício 35) Uma roda varre em ao ser levada ao repouso com aceleração angular constante. Determine a rapidez angular inicial da roda ao começar a ser freada.
Ver solução completaQuestão 39
(Cap 9 – Ex 32) Uma roda-gigante de de raio completa uma volta a cada . (a) Qual é a sua rapidez angular (em radianos por segundo)? (b) Qual é a rapidez linear de um passageiro? (c) Qual é a aceleração de um passageiro?
Ver solução completaQuestão 40
(Capítulo 9.1 – Exercício 28) Uma partícula se move com uma rapidez constante de em um círculo de de raio. (a) Qual é a sua rapidez angular em radianos por segundo em relação ao centro do círculo? (b) Quantas voltas ela dá em ?
Ver solução completaQuestão 41
(Cap 9 – Ex 36) Uma bicicleta tem rodas de de diâmetro. O ciclista acelera a partir do repouso, com aceleração constante, até , em . Qual é a aceleração angular das rodas?
Ver solução completaQuestão 42
Parte 1 – Uma roda de bicicleta é constituída por um aro de raio e por barras que sustentam o aro em torno de um eixo de rotação conforme a figura. A massa do aro vale e de cada uma das barras vale . Determine o momento de inércia desta roda. (O momento de inércia de uma barra girando em torno de seu centro de massa ale ).
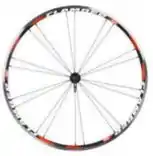
Parte 2 – Uma roda com momento de inércia se encontra girando a uma velocidade angular de . Esta roda é então freada com uma aceleração angular constante de até parar.
a) Determine a energia cinética inicial da roda.
b) Determine o tempo necessário e o ângulo percorrido em radianos até a roda parar.
Parte 3 – Um disco gira no plano com aceleração angular dada por , onde é o tempo.
a) Se o disco possui velocidade angular inicial , escreva a equação para a velocidade angular.
b) Determine o vetor velocidade angular do disco no instante onde .
Ver solução completaQuestão 43
Dois fios ideais estão enrolados na periferia de um cilindro de comprimento , raio e massa . O cilindro é abandonado a partir do repouso e passa a cair na vertical sem escorregar nos fios. Considere e .
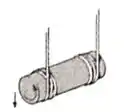
Para o instante em que o eixo do cilindro tiver descido a distância vertical de , calcule:
a) a energia cinética de translação do cilindro;
b) a energia cinética de rotação do cilindro.
Considere agora um segundo cilindro de mesmo , mesmo e mesma massa que o anterior, mas com massa distribuída de modo diferente de tal modo que , onde é um fator adimensional menor ou igual a .
c) Calcule o valor de sabendo que, após cair a partir do repouso, a velocidade escalar de seu centro de massa vale .
Ver solução completaQuestão 44
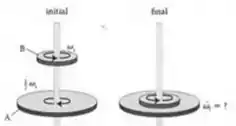
O disco A na figura abaixo, com raio e inércia está inicialmente rodando na direção horária, como visto de cima com uma velocidade angular . O disco , de inércia e raio , está inicialmente rodando na direção anti-horária com velocidade angular . Os dois discos estão restritos a rodar em torno do mesmo eixo, que passa pelo centro de ambos os discos. Há atrito entre os discos, de forma que após entrarem em contato os discos giram com a mesma velocidade angular .
- Qual é a velocidade angular final, , do sistema?
- Determine a variação de energia térmica do sistema composto pelos dois discos.
Questão 45
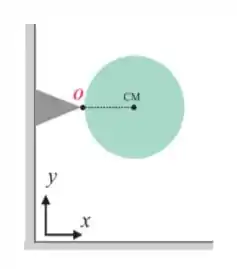
14. Um disco homogêneo de raio e massa está fixo em uma de suas extremidades a uma parede vertical, conforme a figura abaixo. O disco gira, sem atrito, ao redor do eixo fixo que passa pelo ponto O é perpendicular ao plano , sendo abandonado com velocidade inicial nula quando o centro de massa está na altura do eixo de rotação. O módulo do vetor O módulo do vetor velocidade angular do disco quando seu centro estiver diretamente abaixo do eixo de rotação é, em :

Questão 46
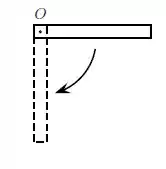
Uma haste fina uniforme e homogênea, de espessura desprezível e comprimento , pode girar livremente em torno de um eixo horizontal que passa pela extremidade da haste e que é perpendicular a ela. Se a haste for liberada na posição horizontal, a partir do repouso, sua velocidade angular quando passar pela posição vertical será igual a
a)
b)
c)
d)
e)
Ver solução completaQuestão 47
Um aro rola sem deslizar com velocidade constante sobre um plano horizontal. O momento de inércia em relação ao seu eixo que passa pelo centro de massa é . Sua energia cinética de rotação é
(A) metade da sua energia cinética de translação.
(B) igual a sua energia cinética de translação.
(C) o dobro da sua energia cinética de translação.
(D) quatro vezes a sua energia cinética de translação.
(E) um terço da sua energia cinética de translação.
Ver solução completaQuestão 48
Considere um corpo rígido constituído por hastes rígidas sem massa e de comprimento e um conjunto de nove esferas de mesma massa (que podem ser consideradas partículas). O sistema pode ser colocado para girar em torno de 3 eixos, indicados na figura: o eixo AB, o eixo CD e o eixo z, que é perpendicular ao plano definido pelo corpo rígido e passa pela esfera do canto inferior direito.
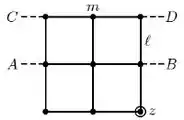
Sabendo que pode-se fornecer sempre a mesma energia de rotação ao corpo rígido, qual a relação entre os módulos das velocidades angulares de rotação em cada um dos 3 casos?
(a
(b
(c)
(d)
(e)
Ver solução completaQuestão 49
Sejam duas massas e penduradas por um fio inextensível de massa desprezível a uma polia ilustrada na figura. A polia consiste um anel de massa e raio e hastes de massa . Veja a figura.
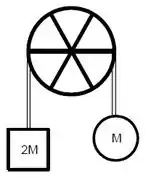
O momento de inércia rotacional da polia em relação ao seu eixo é . O sistema é solto do repouso e o atrito é desprezível.
Determine a variação da energia potencial gravitacional do sistema desde o instante em que foi solto até o instante em que o módulo da velocidade das massas for igual a .
Ver solução completaQuestão 50
Considere duas esferas sólidas idênticas de massa e raio que são abandonadas do repouso e descem 2 planos inclinados de mesmo comprimento, com a mesma inclinação em relação a direção horizontal. Em um dos planos não há atrito entre a esfera e a superfície. No outro plano há atrito e a esfera desce o plano rolando sem deslizar. É correto afirmar que:
(a) A velocidade do centro de massa da esfera ao atingir a base do plano inclinado será maior no caso em que não há atrito.
(b) A velocidade do centro de massa da esfera ao atingir a base do plano inclinado será a mesma nos dois casos pois a energia mecânica se conserva.
(c) A energia cinética da esfera será maior no caso em que há atrito pois ela possui, nesse caso, velocidade angular de rotação.
(d) Nos caso sem atrito a esfera também rola sem deslizar até a base do plano.
Ver solução completaQuestão 51
A hélice ligada ao rotor de um helicóptero é composta de três lâminas com cada uma tendo comprimento de e massa . O rotor gira a revoluções por minuto. Considere cada lâmina como uma haste fina.

Haste:
a) Calcule o momento de inércia do conjunto das lâminas em torno do eixo de rotação.
b) Determine a energia cinética de rotação desse conjunto de três lâminas.
Ver solução completaQuestão 52
O sistema da figura ao lado é constituído por uma barra homogênea de comprimento , e massa , e um anel de raio e massa . Este anel está fixo em uma das extremidades da barra e a outra extremidade pode girar em torno de um eixo de rotação horizontal. Inicialmente o sistema se encontra em repouso, com a barra e o anel em um plano horizontal. O objeto então é liberado e pode girar livremente, sem atrito, em torno do eixo (a figura mostra o objeto na parte mais baixa de sua trajetória)
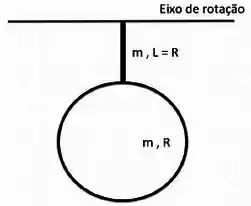
a) Calcule o momento de inércia do objeto em relação ao eixo descrito (dados: momento de inércia da barra em torno de seu centro de massa , momento de inércia do anel com eixo de rotação ao redor de um diâmetro ).
b) Calcule a velocidade angular do objeto ao passar na parte mais baixa da trajetória (Lembre-se, quando a barra se encontra na horizontal o objeto esta em repouso).
Ver solução completaQuestão 53
Partindo simultaneamente do repouso um disco de raio e um anel de raio rolam sem deslizar, descendo uma rampa inclinada, a partir de uma mesma altura da base (medida do ponto de contato dos objetos com a rampa). É correto afirmar que:
(a) Se os dois corpos tiverem a mesma massa a sua energia cinética final será a mesma, independente de quais sejam os seus raios.
(b) Se o anel sempre chegará primeiro na base da rampa, independente de quais sejam as massas dos dois corpos.
(c) Se as massas dos corpos rígidos forem iguais, o anel sempre chegará primeiro na base da rampa, independente de quais sejam os raios.
(d) Se os dois corpos tiverem a mesma massa e mesmo raio, o centro de massa do anel e do disco chegarão à base da rampa com mesma velocidade.
(e) O disco e o anel sempre chegarão na base da rampa ao mesmo tempo, independente de quais sejam as massas e raios.
Ver solução completaQuestão 54
Uma haste uniforme de massa e comprimento é colocada verticalmente acima de um pivô sem atrito, como mostrado na figura abaixo. A partir da vertical, a haste cai para o solo. Com que velocidade a extremidade livre da haste atinge o solo?
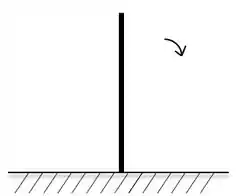
A.
B.
C.
D.
E.
Ver solução completaQuestão 55
Um bloco e um cilindro são lançados, de mesma massa M, com a mesma velocidade escalar v, ao longo de planos que tem a mesma inclinação (diferente de zero), em relação à horizontal. No plano onde está o bloco não há atrito e no plano onde se encontra o cilindro há atrito suficiente para que ele role sem deslizar. Sabendo que o momento de inércia do cilindro relativo ao eixo perpendicular a ele que passa pelo seu centro de massa é. A relação entre a altura máxima que o bloco atinge Hb e a altura máxima que o cilindro atinge HC nos respectivos planos é dada por:
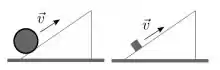
a) , pois tanto a energia mecânica do bloco como a do cilindro se conserva.
b) Hb = Hc, pois tanto a energia cinética do bloco como a do cilindro se conserva.
c) Hb = Hc, pois tanto a energia mecânica do bloco como a do cilindro se conserva.
d) , pois o bloco desliza sem atrito.
e) , pois o momento angular do cilindro se conserva.
f) Não há como afirmar tal relação sem conhecermos o ângulo θ que os planos fazem com a horizontal.
g) , pois tanto a energia mecânica do bloco como a do cilindro se conserva.
Ver solução completaQuestão 56
Qual a energia cinética de rotação da Terra? Os dados sobre a Terra podem ser encontrados em qualquer livro de física básica.
Ver solução completaQuestão 57
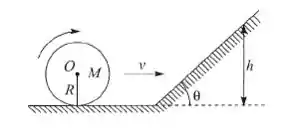
Uma roda cilíndrica homogênea de raio e massa , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade , e sobe sobre um plano inclinado de inclinação , continuando a rolar sem deslizamento. Até que altura o centro da roda subirá sobre o plano inclinado?
Questão 58
Uma esfera sólida sobe rolando um plano inclinado, cujo ângulo de inclinação é igual a em relação a horizontal. Na base do plano, o centro de massa da esfera tem uma velocidade linear de . Seu momento de inércia em relação ao seu centro de massa é .
- Qual é a energia cinética da esfera na base do plano inclinado?
- Qual é a distância que a esfera percorre ao subir o plano?
- A resposta do item b depende da massa da esfera? Comente.
Questão 59
(Capítulo 9.1 – Exercício 31) Um disco de 12 cm de raio, que começa a girar em torno de seu eixo em , gira com uma aceleração angular constante de . Em , (a) qual é a rapidez angular do disco e (b) quais são as componentes tangencial e centrípeta da aceleração de um ponto na borda do disco?
Ver solução completaQuestão 60
Um corpo rola sem deslizar ao longo de um plano inclinado de em relação à horizontal. Sendo o corpo um cilindro e havendo partido do repouso a partir de uma certa altura, observa-se que adquire uma velocidade angular de ao chegar à base do plano inclinado. Se o raio do cilindro é e a massa é , calcule a altura a partir da qual ele começou a rolar.
Ver solução completaQuestão 61
Assinale qual é a afirmativa verdadeira:
a) Para calcularmos o momento de inércia rotacional de um objeto em torno de um eixo, podemos considerar toda a sua massa concentrada no seu centro de massa.
b) O momento de inércia de um corpo rígido em torno de um eixo que passa pelo seu centro de massa é menor que o momento de inércia em torno de qualquer outro eixo paralelo.
c) Se a soma das forças em um objeto for zero, o torque neste objeto provocado por estas forças será zero também.
d) A energia cinética de um corpo girando em torno de um eixo depende somente da sua velocidade angular e da sua massa.
Ver solução completaQuestão 62
O ângulo em radianos descrito pelo eixo de um motor é dado por
Qual o número mínimo de voltas o eixo completa até inverter o sentido da rotação?
Ver solução completaQuestão 63
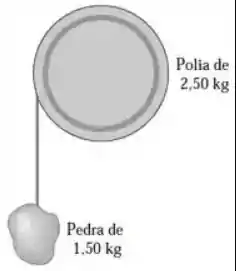
Uma polia sem atrito possui o formato de um disco maciço e uniforme com massa de 2,50 kg e raio de 0,2 m. Uma pedra de 1,5 Kg é presa a um cabo muito leve que envolve a borda da polia, e o sistema é liberado a partir do repouso, imagem abaixo. Qual distância a pedra deve descer para que a polia tenha 4,5 J de energia cinética? Considere o momento de inércia da polia .
Questão 64
A peça de uma máquina tem o formato de uma esfera maciça e uniforme com massa de 225 g. diâmetro de 3,00 cm e momento de inércia em tomo de um eixo que passa pelo seu centro de . Ela está girando em torno de um eixo com atrito desprezível, mas, em um ponto em seu equador, ela está roçando contra uma parte metálica, resultando em uma força de atrito de 0,0200 N nesse ponto. A partir das informações acima descritas, encontre: o módulo, a direção e o sentido da aceleração angular. Deixe claro o sistema de coordenadas utilizado.
Ver solução completaQuestão 65
Para ligar um cortador de grama, você deve puxar uma cordinha que está enrolada ao longo do perímetro de um volante. Depois de você puxar a corda por , o volante está girando a revoluções por segundo quando a cordinha se desprende. Esta tentativa de ligar o cortador não funciona, no entanto, e o volante acaba por parar após do desprendimento da cordinha. Suponha aceleração constante, tanto durante a puxada da cordinha quanto durante o freamento do volante. (a) Determine a aceleração angular média durante os em que a cordinha está sendo puxada e durante os do fretamento do volante. (b) Qual é a maior rapidez angular atingida pelo volante? (c) Determine a razão entre o número de voltas realizadas na primeira etapa e o número de voltas realizadas na segunda etapa.
Ver solução completaQuestão 66
(Capítulo 9.1 – Exercício 37) A fita em um videocassete VHS padrão tem um comprimento total de , o suficiente para operar durante . Quando no início, o carretel cheio tem um raio externo de e um raio interno de . Em algum momento da operação, os dois carretéis têm a mesma rapidez angular. Calcule esta rapidez angular em radianos por segundo e em revoluções por minutos. Dica: Entre os dois carretéis, a fita corre com rapidez constante.

Questão 67
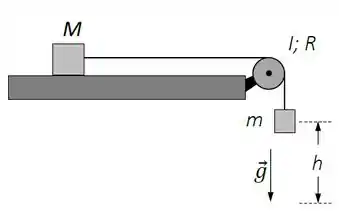
Um bloco de massa encontra-se sobre uma superfície horizontal sem atrito, preso a uma corda que passa por uma roldana circular de raio e momento de inércia (ver Figura 3). A corda não desliza na roldana e sua outra extremidade é presa a um bloco de massa . O sistema encontra-se inicialmente em repouso. Considere .
- Num dado instante após o sistema ser liberado, os blocos possuem velocidade de módulo . Qual é a velocidade angular da roldana nesse instante? Qual é a energia cinética total do sistema formado pelos blocos e pela roldana nesse instante?
- Qual é o módulo da velocidade dos blocos no instante em que o bloco menor se encontra a uma distancia vertical de em relação à sua altura original?
- Na situação do item (b), qual é o módulo do momento angular da roldana em relação ao seu centro?
- Quais são a aceleração dos blocos e a aceleração angular da roldana após o sistema ser liberado?
Questão 68
(Capítulo 9.1 – Exercício 28) Uma partícula se move com uma rapidez constante de em um círculo de de raio. (a) Qual é a sua rapidez angular em radianos por segundo em relação ao centro do círculo? (b) Quantas voltas ela dá em ?
Ver solução completaQuestão 69
(Capítulo 9.1 – Exercício 29) Uma roda, partindo do repouso, gira com aceleração angular constante de . Após da partida: (a) Qual é sua rapidez angular? (b) Qual é o ângulo varrido pela roda? (c) Quantas voltas ela completou? (d) Qual é a rapidez linear e qual é a magnitude da aceleração linear de um ponto distante do eixo de rotação?
Ver solução completaQuestão 70
(Capítulo 9.1 – Exercício 30) Uma mesa giratória, girando a , é levada ao repouso em 26 s. Supondo constante a aceleração angular, encontre (a) a aceleração angular. Durante esses , determine (b) a rapidez angular média e (c) o deslocamento angular em número de voltas.
Ver solução completaQuestão 71
(Cap 9 – Ex 117) Um disco uniforme de raio e massa gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano vertical. Ele é largado do repouso, com seu centro de massa à mesma altura do pivô. (a) Qual é a rapidez angular do disco, quando seu centro de massa está diretamente abaixo do pivô? (b) Qual é a força exercida pelo pivô sobre o disco neste momento?
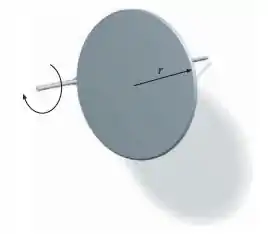
Questão 72
(Capítulo 9.1 – Exercício 33) Um ciclista acelera uniformemente a partir do repouso. Após , as rodas completam . (a) Qual é a aceleração angular das rodas? (b) Qual é a rapidez angular das rodas ao final dos ?
Ver solução completaQuestão 73
(Cap 11 – Ex 1) Um carro se move a em uma estrada plana no sentido positivo de um eixo . Os pneus tês um diâmetro de . Em relação a uma mulher viajando no carro e em termos dos vetores unitários, qual é a velocidade
a) no centro,
b) no alto e na
c) base de cada pneu e o módulo da aceleração
d) no centro, e
e) no alto e
f) na base de cada pneu? Em relação a uma pessoa parada no acostamento da estrada e em termos dos vetores unitários, qual é a velocidade
g) no centro,
h) no alto e na
i) base de cada pneu e o módulo da aceleração
j) no centro, e
k) no alto e
l) na base de cada pneu?
Ver solução completaQuestão 74
Seja um corpo na forma de um formado por duas barras finas de comprimento e massa como ilustra a figura ao lado. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na vista frontal indicada .
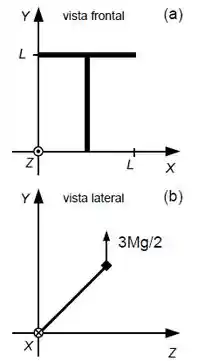
- Determine o momento de inércia rotacional do corpo em torno do eixo e a posição do seu centro de massa na posição indicada na figura em função dos dados do problema.
- O corpo é girado em torno do eixo e colocado na posição mostrada na vista lateral . O eixo positivo na vista lateral aponta para dentro do plano do papel. O corpo faz com o plano onde permanece em equilíbrio estático com a ajuda da força . Determine a força que o eixo faz no corpo nesta posição em função dos dados do problema.
- Suponha agora que a força pare de atuar e que o corpo, a partir da posição do item anterior, passe a girar livremente em torno do eixo , partindo do repouso. Determine a energia cinética do copro quando ele cruzar o plano .
Questão 75
Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:
onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .
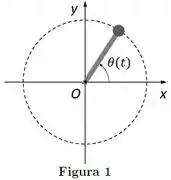
A energia cinética de rotação da partícula no instante vale:
(a) J (b) J (c) J (d) J (e) J (f) J (g) J (h) J
Ver solução completaQuestão 76
Uma bola de basquete (massa M = 600g e raio R= 12,0cm) sobe um plano inclinado (θ = 30) rolando sem deslizar. Na base do plano, o topo da esfera tem velocidade v = 5,00m/s.
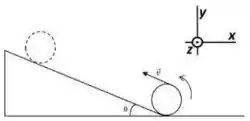
c) Calcule o trabalho total sobre a bola necessário para fazê-la parar.
d) Calcule a distância D que a bola percorre ao longo do plano inclinado até parar.
Ver solução completaQuestão 77
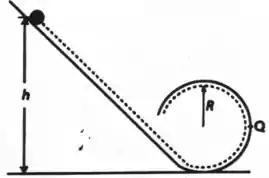
Uma bola de gude de massa e raio rola sem deslizar ao longo do trilho curvo mostrado na figura, tendo sido abandonada do repouso em algum lugar sobre a parte reta do trilho. A linha pontilhada descreve a trajetória do centro de massa da bola de gude.
Dado: Momento de inércia de uma esfera girando ao redor do eixo que passa pelo seu centro de massa:
- Desenha as forças que agem sobre a esfera quando ela desce a parte reta do trilho, justificando o sentido da força de atrito.
- De que altura mínima acima da base do trilho se deve abandonar a bola a fim de que ela se mantenha no trilho no topo da circunferência?
- Se a bola é abandonada de uma altura acima da base do trilho, qual será o módulo da componente horizontal da força atuante sobre ela no ponto
Questão 78
Uma roda rola sem deslizar ao longo de uma estrada horizontal, como mostrado na figura abaixo. A velocidade instantânea do centro da roda é representada por em relação à estrada. Neste referencial, as velocidades instantâneas do ponto mais alto da roda e do ponto em contato com a estrada são dadas respectivamente por:
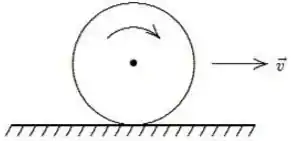
a) e zero.
b) e
c) e
d) zero e
e) nenhuma das anteriores.
Ver solução completaQuestão 79
Um cilindro uniforme, uma esfera, e um tubo (oco) são lançados horizontalmente, com a mesma velocidade, em uma superfície plana, em direção a um plano inclinado. Os três tem o mesmo raio, e rolam sem deslizar. Qual deles atinge uma altura maior no plano inclinado?
a) É necessário saber as massas para realizar o cálculo.
b) A esfera.
c) Os três atingem a mesma altura.
d) O tubo oco.
e) O cilindro maciço.

Questão 80
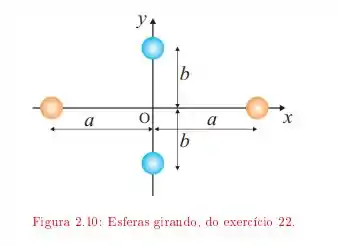
Quatro esferas pequenas de massa m estão presas às extremidades de uma estrutura de massa desprezível no plano xy.
a. Se a rotação do sistema ocorre ao redor do eixo y com velocidade angular ω, encontre o momento de inércia Iy ao redor do eixo y e a energia cinética rotacional ao redor desse eixo.
Questão 81
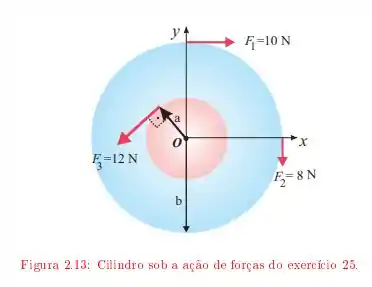
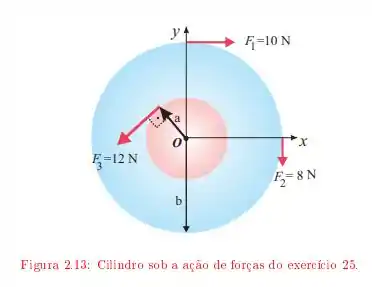
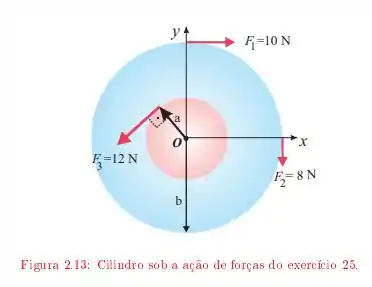
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Qual é o vetor aceleração angular do cilindro?
Questão 82
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Determine o ângulo total que o cilindro gira em . Verifique que o trabalho efetuado pelo torque é igual a energia cinética.
Questão 83
Roda mundo, roda gigante
Roda moinho, roda pião
O tempo rodou num instante
Nas voltas do meu coração...
Trecho da música Roda Viva de Chico Buarque.
Nesta música, Chico Buarque, trata do turbilhão que novas vidas se transformam. Neste trecho, especificamente, temos destacados movimentos de rotação. Sabemos que todo movimento de rotação está associado à aceleração centrípeta, que tem como fórmula: onde é a velocidade e é o raio.
O movimento de rotação tem uma ligação com a grandeza física:
(a) Impulso.
(b) Energia Cinética.
(c) Potência.
(d) Momento Linear
(e) Energia Potencial.
Ver solução completaQuestão 84
A figura abaixo mostra dois ioiôs de mesmo tamanho (raios iguais) e mesma massa, que podem descer rolando por uma corda que os prende ao teto. As cordas são inextensíveis e não deslizam.
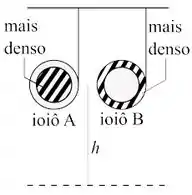
Cada ioiô é composto dos mesmos dois materiais, um mais denso que o outro (ou seja, com uma massa maior por unidade de volume).
No ioiô o material mais denso forma a metade interna da área do disco. No ioiô ele forma a metade externa da área do disco.
Os dois ioiôs são largados a partir do repouso.
Após eles descerem rolando uma mesma altura , o que podemos afirmar sobre as energias cinéticas, e , as velocidades dos centros de massa, e , e as velocidades angulares e dos ioiôs e respectivamente?
Questão 85
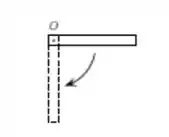
Uma barra uniforme de comprimento e massa está pressa por uma das extremidades a um pivot com atrito desprezível, e, livre para girar no plano vertical. A barra é liberada do repouso na posição horizontal como mostra a figura. Ao atingir a posição vertical, a velocidade linear da extremidade da barra oposta ao pino é
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 86
Um cilindro de raio e massa rola sem deslizar numa superfície horizontal, com velocidade . Num certo instante, ele começa a subir um plano inclinado de ângulo e continua rolando sem deslizar até parar. A altura até a qual o cilindro sobe antes de parar é:
a)
b)
c)
d)
e) nenhuma das anteriores
Dados:
Momento de inércia de um cilindro:
Ver solução completaQuestão 87
Um cilindro de massa e raio R faz parte de um motor e roda em torno de seu eixo de simetria. A velocidade de um ponto na borda do disco é . Qual a energia cinética do cilindro?
a)
b)
c)
d)
e) nenhuma das anteriores
Ver solução completaQuestão 88
Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Utilize que .
A velocidade da extremidade superior da barra imediatamente antes de tocar o solo é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 89
O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.
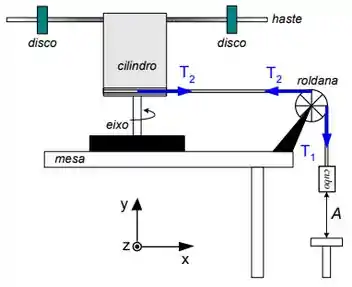
(d) Determine a energia cinética adquirida pelo sistema desde até quando o cubo está prestes a encostar no suporte. Despreze atritos.
Ver solução completaQuestão 90
Uma placa não-uniforme de massa está inicialmente em repouso no plano vertical, podendo girar sem atrito sobre um eixo perpendicular ao plano que passa pelo ponto .
Seu centro de massa (CM) está a uma altura do eixo, e o ponto em sua extremidade está a uma altura do eixo. Seu momento de inércia em relação ao eixo que passa pelo ponto é .
Partindo do repouso, a placa cai sob efeito da aceleração gravitacional , girando sobre o ponto , conforme a figura.
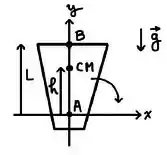
Quando o ponto passa pelo eixo , sua velocidade é:
Questão 91
Um disco fino, homogêneo, de massa 100 g e 8,0 cm de diâmetro gira em torno de um eixo perpendicular ao seu plano que passa pelo seu centro. A energia cinética de rotação do disco é de 0,15 J. Qual o módulo da velocidade de um ponto na borda do disco?
Ver solução completaQuestão 92
Seja um corpo na forma de um quadrado de lado composto por hastes finas com massas indicadas na figura. Na figura está também indicado o sistema de coordenadas a ser utilizado. O corpo pode girar livremente sem atrito em torno do eixo e encontra-se em repouso na posição indicada.
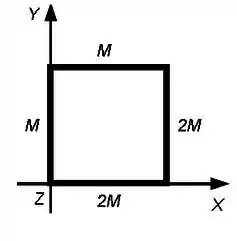
(b) Determine a posição do centro de massa do corpo em função dos dados do problema na posição indicada na figura.
(c) O corpo passa a girar em torno do eixo . Determine o módulo de sua velocidade angular máxima . Em que posição ela ocorre? Suponha que , e .
(d) Determine a velocidade linerar na extremidade do corpo oposta ao eixo na mesma posição do item anterior.
Ver solução completaQuestão 93
A partícula da esquerda, de massa , está unida à partícula da direita, de massa , por uma haste rígida de massa desprezível. O comprimento da haste é . O conjunto está girando com velocidade angular em torno de um eixo perpendicular à haste passando pelo centro de massa do sistema. A energia de rotação em torno do centro de massa é:

(a)
(b)
(b)
(b)
(b)
Ver solução completaQuestão 94
Um corpo rígido é formado por três barras finas de comprimento , unidas na forma de uma letra . O corpo pode girar livremente em torno de um eixo horizontal que coincide com uma das "pernas"do . O corpo é liberado a partir do repouso em uma posição em que o plano de está na horizontal. Qual é a velocidade angular do corpo quando o plano do está na vertical?
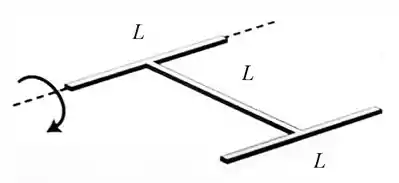
A.
B.
C.
D.
E.
Ver solução completaQuestão 95
Três forças são aplicadas a uma roda com raio igual a 0,35 m, conforme mostra a figura. Uma força é perpendicular à borda, outra é tangente a ela e a outra forma um ângulo de 40º com o raio. Qual é o torque resultante da roda produzido por essas três forças em relação a um eixo perpendicular à roda e que passa através de seu centro?
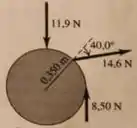
Questão 96
(Capítulo 9.1 – Exercício 29) Uma roda, partindo do repouso, gira com aceleração angular constante de . Após da partida: (a) Qual é sua rapidez angular? (b) Qual é o ângulo varrido pela roda? (c) Quantas voltas ela completou? (d) Qual é a rapidez linear e qual é a magnitude da aceleração linear de um ponto distante do eixo de rotação?
Ver solução completaQuestão 97
(Capítulo 9.1 – Exercício 64) As partículas da figura estão ligadas por uma barra muito leve. Elas giram em torno do eixo a . (a) Determine a rapidez de cada partícula e utilize esses valores para calcular a energia cinética do sistema diretamente a partir de . (b) Determine o momento de inérica em relação ao eixo , calcule a energia cinética a partir de e compare seu resultado com o resultado da parte (a).
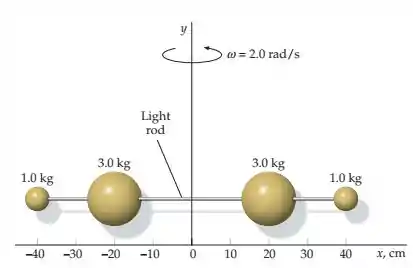
Questão 98
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Qual é a sua energia cinética depois de ?
Questão 99
Um satélite artificial descreve uma órbita circular de raio em torno da Terra e realiza voltas em um dia.
Para que este satélite seja geoestacionário, ou seja, fique parado em relação a um ponto na superfície da Terra, ele deve circular em outra órbita. Determine o raio da nova órbita em função de .
As energias mecânicas do satélite nessas órbitas são iguais? Determine a razão entre a Energia Mecânica na órbita de raio e a Energia Mecânica na órbita de raio e justifique sua resposta.
Ver solução completa