Cálculo do Potencial a partir do Campo Elétrico
Produzido por Bruno SoaresTeoria
Introdução
Vimos que o método da integral dos potenciais gerado por cargas infinitesimais calculou legal o potencial elétrico de uma distribuição em linha e também de uma superficial, mas e se o corpo carregado tiver essa carinha aqui?
Temos uma esfera condutora de raio carregada com uma carga total e queremos calcular o potencial elétrico num ponto que está fora da esfera, há uma distância do centro da esfera.
Nesse caso, se tentássemos fazer pela integral de cada carga da esfera, não iríamos conseguir calcular, daria muito trabalho!
Mas sabemos como calcular o campo elétrico gerado por essa esfera usando a Lei de Gauss! Será que podemos usar esse campo para encontrar o potencial?!
A resposta é que sim e, para isso, usaremos o método da integral de linha do campo elétrico, onde:
A nossa estratégia aqui é a seguinte:
- Usamos a Lei de Gauss e calculamos o campo elétrico;
- Utilizamos o campo elétrico para calcular o potencial elétrico.
Esfera Carregada
Para calcular o campo elétrico, pela Lei de Gauss, o primeiro passo é criar nossa Superfície Gaussiana, que nesse caso será uma superfície esférica de raio .
Aplicando Gauss (se você não lembra de Gauss, dá uma revisada que vai ser importante aqui), nós chegaríamos em:
Sabendo que esse campo é radial e aponta para fora da esfera, podemos escrevê-lo vetorialmente:
Onde o vai ser a própria carga total da esfera e é a nossa constante eletrostática .
Substituindo o campo na equação do potencial elétrico temos:
E como o vetor campo elétrico está na mesma direção que o vetor , o produto escalar entre os dois será o produto dos seus módulos:
E tirando o que é constante da integral, teremos:
Agora para encontrar o potencial em um ponto, a estratégia é fazer com que seja o potencial no infinito, que por convenção é .
Show, e para encontrar o potencial em um ponto dado por uma distância do centro da esfera, a gente escreve assim:
Agora é só realizar a conta dessa integral!
E substituindo os limites de integração:
Aonde um número dividido por infinito, a gente pode lembrar lá de limites que ele vai dar zero, logo:
Isso é válido para um , ou seja, fora da esfera.
E se quiséssemos saber o potencial dentro da esfera, em um ponto que está no interior da esfera:
Nesse caso, precisamos conhecer o campo elétrico no interior da esfera, para um .
Aqui nesse exemplo, estamos usando uma esfera condutora, e dentro de corpos condutores o campo elétrico é SEMPRE nulo:
(se a esfera não fosse condutora, você ia precisar aplicar a lei de gauss de novo, para encontrar esse campo no interior da esfera, beleza?)
Agora vamos fazer:
Usando , e , teremos:
Repara que nessa integral estamos caminhando lá do infinito até uma distância que está dentro da esfera.
E esse campo tem uma cara fora da esfera e outra cara dentro da esfera, então precisamos abrir essa integral em duas:
Repara que os limites de integração são de até para dentro da esfera e de até o infinito para fora da esfera.
Agora é só substituir o campo no interior e o campo no exterior da esfera e depois integrar:
Chegando finalmente em:
Isso é válido para .
Ou seja, o potencial elétrico dentro da esfera condutora é um valor constante dado por essa expressão aí em cima.
Sendo assim, o potencial elétrico da esfera condutora é dado por:
Graficamente, o potencial elétrico gerado por essa esfera, é algo assim:
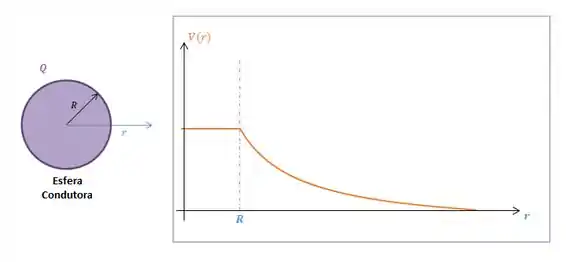
Ou seja, no interior da esfera é constante e fora da esfera o potencial vai caindo.
Repara só, que lá no infinito, com , o potencial tende a zero, assim como a gente tinha estipulado!
Aqui nós vimos como calcular o potencial elétrico gerado por uma esfera condutora, mas podemos fazer o mesmo procedimento para cilindros, planos e esferas, condutores ou isolantes! Ou seja, tudo que podemos aplicar a Lei de Gauss para conhecer o campo, conseguimos conhecer o potencial também!
Diferença de Potencial em Capacitores
O método da integral de linha também é utilizado para se calcular a diferença de potencial entre as placas de um capacitor. Se você não conhece um capacitor ainda, tem uma matéria aqui no Responde Aí explicando o que eles são!
Existem basicamente 3 tipos de capacitores: Capacitor de placas planas, cilíndrico e esférico.
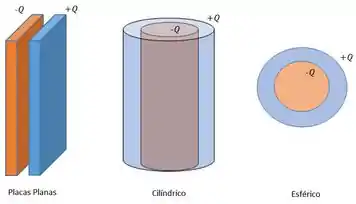
Vamos dar uma olhada em como calcular o potencial de um capacitor cilíndrico!
O capacitor cilíndrico é formado por duas superfícies cilíndricas, onde uma está carregada com carga e a outra com carga .
Para encontrar a diferença de potencial entre as superfícies, faremos:
Onde é o raio do cilindro de dentro e é o raio do cilindro de fora.
E para encontrar o campo entre as placas, aplicaremos a Lei de Gauss, fazendo uma superfície gaussiana cilíndrica entre os cilindros:
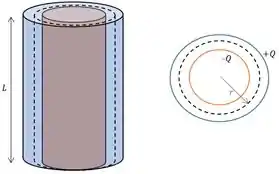
Como o campo é constante ao longo da gaussiana e está paralelo com o vetor , teremos:
Lembrando que essa área, para o caso da simetria cilíndrica, é a área lateral do cilindro apenas:
E a carga interna à superfície Gaussiana, será a carga do cilindro interno , com isso teremos:
E podemos ainda, escrevê-lo vetorialmente:
E substituindo o campo na expressão do potencial, temos:
Esse produto escalar entre os vetores, vai dar apenas a multiplicação dos módulos e além disso, podemos tirar o que é constante da integral:
E resolvendo essa integral, teremos:
E aí, é só substituir os limites:
E pra finalizar, vamos usar uma propriedade do logaritmo que diz que a subtração de logaritmos é o logaritmo da divisão:
E essa é a diferença de potencial em um capacitor cilíndrico.
Para encontrar esse cara para o capacitor plano ou o esférico, a ideia é sempre a mesma, encontrar o campo por Gauss e depois encontrar o potencial com a relação que aprendemos aqui!
Bora praticar!?
Diferença de Potencial em Capacitores
Exercícios Resolvidos
Exercício Resolvido #1
USP-P1-2012-3 - Modificada
O eixo de um cilindro condutor de de raio dista do plano conforme a figura. O cilindro é infinito na direção perpendicular ao plano da figura e todo o semiespaço é preenchido com um material condutor.
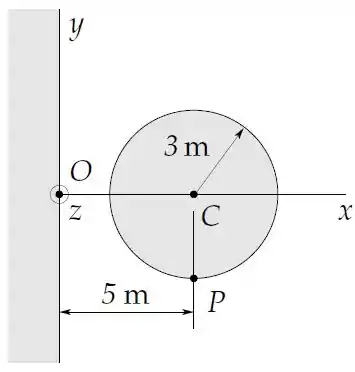
O potencial eletrostático num ponto de coordenadas no espaço fora dos condutores é dado por
onde e são em metros.
Determine o potencial no ponto do eixo do cilindro condutor .
Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.
Passo 1
Determine o potencial no ponto do eixo do cilindro condutor .
O potencial que o exercício nos deu é
Só que esse potencial só serve pra região FORA dos condutores!
Mas tem um macete aqui! Lembra que o potencial dentro de condutores tem que ser constante (já que o campo elétrico no seu interior é nulo)? Então isso significa que o potencial na borda do cilindro é igual ao potencial no seu centro, ou seja
Então pra calcular o potencial no centro do cilindro, basta calcular o potencial no ponto .
Olhando a figura as coordenadas do ponto são . Substituindo essas coordenadas no potencial temos
Assim o potencial no ponto será
Passo 2
Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.
Por definição:
Onde:
Pra descobrir cada componente do campo elétrico, temos que derivar parcialmente em função de cada uma das coordenadas e .
Por fim, o problema pede pra calcular também o campo no interior dos condutores... aí tem um detalhe que você jamais pode esquecer: o campo elétrico no interior de um condutor é sempre nulo!
Resposta
Fora dos condutores
Dentro dos condutores
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 100-13.
Determine (a) a carga e (b) a densidade superficial de cargas de uma esfera condutora de de raio cujo potencial é (tomando no infinito).
Passo 1
Lembrar que o campo elétrico gerado por uma esfera condutora nas regiões localizadas fora da esfera possui uma fórmula muito parecida com a clássica lei de Coulomb para corpos puntiformes:
Passo 2
O potencial do campo elétrico de é constante tanto na superfície da esfera condutora quanto em seu interior e isso ocorre porque não há campo elétrico dentro da esfera, apenas na superfície dela.
Esse campo pode ser calculado por meio da integral:
Passo 3
Logo, a carga vale:
Passo 4
Para acharmos a densidade superficial, basta dividir a carga pela área da esfera:
Resposta
(a)
(b)
Exercício Resolvido #3
Elaboração Própria
Um cilindro condutor infinito ao longo do eixo de raio tem densidade de carga constante . Calcule o potencial a uma distância do eixo do cilindro, dado que a uma distância ele vale . O potencial dado poderia ter sido no infinito?
Passo 1
Rascunhando a situação, temos:
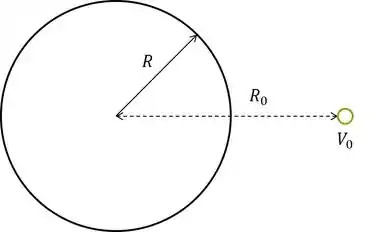
Como essa questão é a cara da Lei de Gauss para calcular o campo, vamos preferir utilizar a fórmula:
Escolhendo um caminho radial em direção ao cilindro. Estabelecido isso, vamos partir para calcular o campo. enunciando a Lei de Gauss:
Pela simetria cilíndrica do problema, escolhemos uma Gaussiana cilíndrica de raio arbitrário e comprimento arbitrário . Dado que escolhemos uma superfície com essas dimensões e já aproveitamos a simetria do campo, temos que o vetores normais à parte lateral da superfície são paralelos ao campo, ao passo que os vetores normais nas tampas são perpendiculares a ele, de forma que:
De forma que:
Portanto:
Passo 2
Pela configuração do campo, o seu módulo é constante em toda parte lateral da Gaussiana:
E temos então a área da lateral com nossa integral:
A expressão para a área lateral é dada pela fórmula:
Logo, temos:
Passo 3
Temos uma densidade linear constante, portanto é válido dizer que a razão entre a carga interna à Gaussiana e o comprimento dela é igual à densidade:
Logo temos:
Substituindo na expressão do campo:
Ainda pela questão da simetria, temos que o campo vai ter somente essa componente radial, então:
Passo 4
Partindo do ponto dado para um ponto arbitrário com distância até o centro, escolhemos um caminho qualquer.
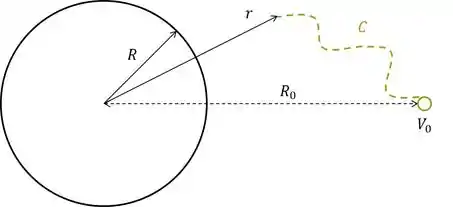
O caminho pode sim ser qualquer um, como na figura, mas se você quiser evitar do examinador da prova exigir uma demonstração desse fato, talvez você queira particularizar e dizer que o caminho é radial, daí nesse caso temos que o campo e o seu vetor são sempre paralelos ao longo do caminho. Aplicando na fórmula, temos:
Arrumando:
E é isso. Mas e aí, poderia ter sido arbitrado no infinito esse potencial inicial? Não, pois a integral não aceitaria . Você estaria tentando fazer:
Coisa que não daria certo, pois é infinito também.
Resposta
Exercício Resolvido #4
Elaboração Própria
Dado uma esfera condutora de raio e carga envolta por uma casca esférica condutora neutra de raios interno e externo iguais a e . Dado que o potencial no infinito é nulo, calcule o potencial em cada região:
Passo 1
Como estamos com um problema de achar o potencial de uma distribuição de cargas que aparentemente morre com Lei de Gauss, vamos preferir usar a fórmula:
Escolhendo um caminho radial, porque é mais fácil de fazer a conta. Afinal, o caminho não importa, certo?
Então a primeira coisa é achar o campo em todas as regiões. Fazendo a Lei de Gauss...
Pela simetria esférica do problema, escolhemos uma superfície esférica de raio arbitrário para ser nossa Gaussiana . Dessa forma, os vetores normais são paralelos ao campo em todos os pontos de , do que segue o fato:
Passo 2
Além disso, pela configuração do campo, temos que o seu módulo é constante em toda , do que segue o fato:
Da última equação, segue que a integral de em toda é a área da Gaussiana. A área superficial de uma esfera é conhecida e é igual à:
Substituindo na Lei, temos:
Passo 3
Vamos matar todas as regiões então. Na região , temos a parte maciça de um condutor, portanto:
Na parte de estamos fora da esfera, logo a carga total é :
Na parte em que estamos dentro da casca esférica. Só que como ela é condutora, não temos campo:
Já na região é só ver o quanto de carga total nós temos, que no caso é só proveniente da esfera:
Portanto:
Passo 4
Agora vamos fazer a conta partindo de um lugar cujo potencial nós conhecemos. No caso o enunciado nos deu o potencial no infinito, então vamos começar nosso caminho partindo de lá para algum ponto em que :
Plugando o campo correspondente à região na equação:
Que resulta em:
Ou seja, mesma coisa que a carga pontual.
Passo 5
Agora vamos partir para a região , que tem outra expressão do campo elétrico. A parada é partirmos de um ponto onde conhecemos o potencial, mas como obtivemos a expressão do potencial no passo anterior, podemos usá-la.
CUIDADO com os limites de integração! Plugando o campo e o potencial conhecidos:
Fazendo:
Logo:
Passo 6
Partindo agora de um ponto na superfície em que vamos para a região . O potencial nesse ponto é só substituir na expressão encontrada anteriormente, ou perceber que não depende de :
Logo, integramos novamente:
Passo 7
Mesma coisa, só que agora partindo da superfície , e vamos para :
Resposta
Exercício Resolvido #5
UNICAMP-P1-2007.2-4
Uma casca esférica condutora de raio interno e externo é concêntrica a uma casca esférica condutora fina de raio . A casca esférica fina tem uma carga total e a carga total da casca externa é zero, sendo que ambas estão isoladas.
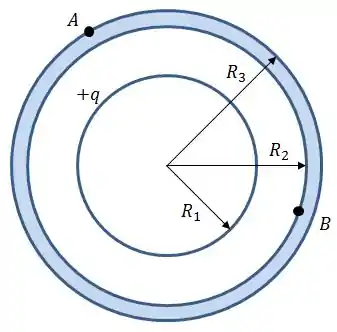
Determine a densidade de carga em cada superfície da camada;
Encontre as expressões para o potencial elétrico em todo espaço: , , e . Suponha que no infinito;
Calcule a diferença de potencial entre os ponto e na camada esférica externa;
Passo 1
Determine a densidade de carga em cada superfície da camada;
O que vai acontecer aqui é o seguinte... no condutor, a resistência do material tende a zero, isso significa que os elétrons podem viajar tranquilamente no interior do condutor, quando excitados por um campo elétrico, no caso.
Assim, como temos uma casca fina de carga no interior da camada esférica, essa carga vai induzir uma concentração de carga negativa igual a na superfície interna.
Entretanto, a carga total do condutor não pode ser alterada, isso quer dizer que, se a superfície interna terá carga , para que a carga total do condutor continue nula, a carga na superfície externa deverá ter carga :
Logo:
Passo 2
Por definição, a densidade superficial de carga é dada por:
Em que é a área da superfície esférica.
Logo:
Passo 3
Encontre as expressões para o potencial elétrico em todo espaço: , , e . Suponha que no infinito;
Para todos os casos, o campo elétrico pode ser determinado pela Lei de Gauss
Como o problema possui uma geometria esférica, o campo elétrico vai ser sempre essa cara:
Por definição, o potencial elétrico é dado por:
Nesse caso:
Lembrando que é .
Onde é o ponto inicial e é o ponto final.
Agora o que precisamos fazer é aplicar isso a cada caso.
Passo 4
Nós vamos começar pela região mais externa, pois a ideia é ir usando os potenciais das regiões externas para descobrirmos os potenciais das regiões mais internas.
Pra tentar facilitar a nossa vida, vamos nomear alguns outros pontos aqui:
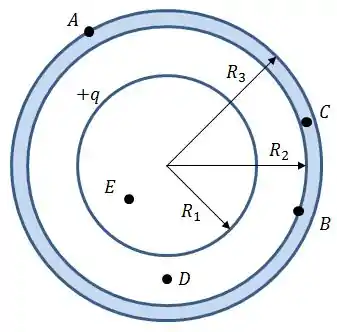
Essa região corresponde ao interior do condutor... então preciso te lembrar de algo que você tem que prometer pra mim que vai carregar contigo pela vida inteira... no interior de um condutor, o campo elétrico é SEMPRE igual a zero, portanto:
Nessa região, como não temos nenhuma carga interna,
Passo 5
Calcule a diferença de potencial entre os ponto e na camada esférica externa;
Entre as superfícies do condutor, como não há campo elétrico:
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
USP-P1-2015-2.
Uma esfera condutora de raio e com carga é envolta por uma camada esférica isolante de raio interno e externo com densidade de carga volumétrica constante.
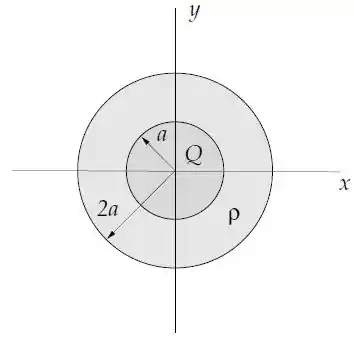
Determine o vetor campo elétrico em todo o espaço;
Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;
Passo 1
Determine o vetor campo elétrico em todo o espaço;
É aquele esquema... viu uma esfera e o cara te pediu o campo elétrico, você pensa logo em Lei de Gauss:
A partir da simetria esférica do problema, já podemos concluir algumas coisas... a primeira delas é que podemos simplificar a Le ide Gauss para:
Outra coisa é que, por causa da sua simetria, o campo elétrico estará sempre na direção radial, logo:
Assim, para qualquer região, teremos apenas que calcular a carga interna e substituir na expressão acima.
Passo 2
Essa região engloba a parte interna da esfera. Como a esfera é condutora, toda a sua carga encontra-se na superfície , logo, quando
Essa região engloba a esfera e parte da casca isolante. Assim, a carga interna aqui será a soma da carga da esfera com a carga de parte da casca esférica.
Para determinar a carga de parte da casca esférica, basta usar a densidade volumétrica de carga:
Portanto, a carga interna total será:
Agora é só substituir na equação do campo elétrico:
Essas regiões intermediárias costumam dar mais trabalho mesmo... relaxa, o resto costuma ser um pouco mais tranquilo.
Essa região engloba a coisa toda. Tínhamos encontrado a seguinte expressão para a carga interna no tópico acima:
A pra calcular a carga interna, basta usar :
Agora é só alegria:
Passo 3
Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;
Por definição, o potencia elétrico é dado por:
Como tanto quanto estão na direção radial, podemos simplesmente escrever:
Então agora o esquema é aplicar isso pra cada região, partindo do infinito. A ideia é sempre começar do infinito até a maior região e, a partir disso, ir usando os resultados anteriores para calcular os potenciais das próximas regiões.
Se liga:
Aqui vamos usar para o caso em que .
Aqui usamos para o caso em que , logo:
Resposta
Resposta
Ei, a resposta está no passo a passo :)