Capacitância Elétrica
Produzido por Bruno SoaresTeoria
A capacitância nada mais é do que a capacidade de um capacitor armazenar carga. Quanto maior for capacitância, que chamamos de
Fórmula da Capacitância
A capacitância é definida da seguinte maneira:
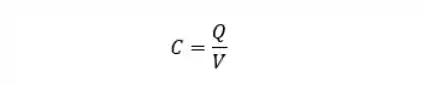
Onde:
é o módulo da carga elétrica armazenada no capacitor; é o módulo da diferença de potencial entre os condutores que compõe o capacitor.
Como Calcular a Capacitância
O fato mais importante sobre a capacitância é o seguinte: ela é uma constante que depende apenas da geometria do capacitor!
Então na prática dificilmente vamos usar a fórmula que terminamos de ver!
-Mas que fórmula eu uso então?! 😖
Calma, eu tenho uma tabelinha com as fórmulas de capacitância pras geometrias mais comuns! Ou seja, quando temos um capacitor plano, esférico ou cilíndrico.
Está aí a tabela pra você:
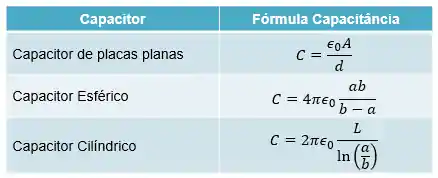
Só precisamos fazer algumas observações sobre essa tabela:
- Capacitor de placas planas:
é a área das placas e é a distância entre as placas;
- Capacitor esférico:
é o raio do cilindro e é o raio interno da casca cilíndrica e é o comprimento;
- Capacitor cilíndrico:
é o raio da esfera e é o raio interno da casca esférica.
Mas afinal de contas, o que é um capacitor? Qual é a cara dele?!
Capacitor
Um capacitor é um sistema constituído por dois condutores separados por um isolante ou vácuo. O isolante pode ser um plástico, ar, etc. Sua função é armazenar carga elétrica para ser usada depois.
O capacitor mais comum é o formado por dois planos separados por uma distância,
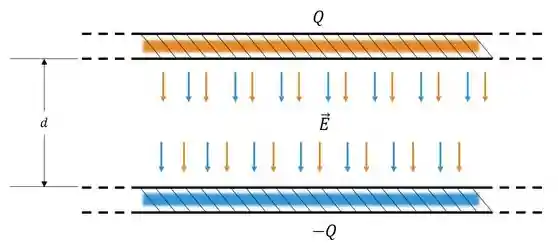
Mas também podemos ter uma esfera concêntrica com uma casca esférica (vácuo ou ar entre eles):
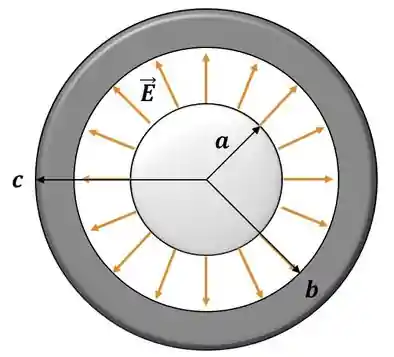
Ou até um cilindro concêntrico com uma casca cilíndrica também.
Capacitância de Um Sistema: Vídeo Aula
Agora pra fechar com chave de ouro, se liga nesse resumo em vídeo super completo sobre a capacitância de um sistema! 👇
Agora que você sabe tudo sobre capacitância, bora praticar com exercícios?
Capacitor
Capacitância de Um Sistema: Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.
Um capacitor de placas paralelas tem placas metálicas quadradas de lados com de comprimento, separadas por .
a) Calcule a capacitância deste dispositivo.
b) Quando este capacitor é carregado com , quanta carga é transferida de uma placa para a outra?
Passo 1
a) Vamos usar pra calcular a capacitância desse dispositivo, beleza?
Mas antes disso vamos converter as unidades pra metros, temos a o lado da placa quadrada e temos a distância entre as placas:
Assim, podemos calcular a área das placas. Como elas são quadradas, temos:
Vamos lembrar também que é uma constante que vale .
Passo 2
Agora sim bora substituir os valores na fórmula:
Passo 3
b) A carga vai ser dada por , sendo que o enunciado deu pra gente e a gente calculou no item a :D
Então
Resposta
Exercício Resolvido #2
UECE – 2008/1
Um capacitor tem uma capacitância de . Se o potencial elétrico entre suas placas for , o número de elétrons em excesso na sua placa negativa é (considere a carga de um elétron sendo ):
a) b) c) d) e) Nenhuma das alternativas.
Passo 1
Vimos que a capacitância é dada por
Mas devemos lembrar também que a carga vai ser sempre um múltiplo da carga fundamental do elétron, ou seja:
Então é só a gente substituir os valores na formulazinha de capacitância para encontrarmos , que vai ser o número de elétrons na placa :)
Passo 2
A nossa fórmula vai ficar assim
Substituindo os valores:
Repare que tiramos o sinal negativo porque estamos falando do número de cargas, e isso não pode ser um valor negativo, é sempre dado em módulo ;)
A nossa alternativa correta é a letra C.
Resposta
c)
Exercício Resolvido #3
UFC - 2002
A figura abaixo representa o processo de descarga de um capacitor como função do tempo. No tempo , a diferença de potencial entre as placas do capacitor era . No instante de tempo , assinalado no gráfico, a diferença de potencial, em volts, entre as placas do capacitor é:
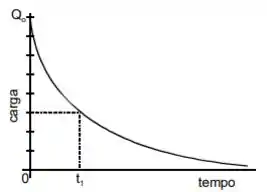
a) b) c) d) e)
Passo 1
No instante , a gente sabe que , e se a gente contar as linhazinhas do gráfico, a carga é . Então a gente pode usar a fórmula pra calcular a capacitância.
Aí no tempo , a carga é , e a capacitância a gente já sabe, ela continua a mesma porque é o mesmo capacitor. Então a gente consegue achar o :)
Passo 2
Em temos que
Então, em :
Boaa! Nossa alternativa correta é a letra C!!
Resposta
c)
Exercício Resolvido #4
Elaboração Própria
Considere duas placas condutoras circulares de área separadas por uma distância no vácuo, cada uma com densidade de carga constante iguais à e . Suponha que a distância seja desprezível se comparada com as dimensões das placas. Calcule a capacitância desse sistema.
Passo 1
Bom, foi pedida a capacitância, então vamos colocar a sua fórmula na mesa:
Show, agora basta encontrarmos os valores de e para o sistema. Vamos começar por pois parece mais simples. Sabe-se que a densidade de carga superficial, por ser constante, é igual à:
Portanto podemos substituir:
Passo 2
Agora vamos tentar calcular a diferença de potencial entre as duas placas. A fórmula que nos dá direto a diferença de potencial (d.d.p.) é a seguinte:
Onde vai ser um caminho retilíneo entre as duas placas. No caso, como só nos importa o módulo da d.d.p. podemos ignorar esse sinal de menos na frente da integral, portanto:
Passo 3
Dado que estamos tratando de duas placas planas, podemos aproximar seu campo por o de um plano infinito. Tacando a Lei de Gauss:
Escolhemos uma gaussiana em forma de cilindro com área de sua seção reta. Como existe fluxo tanto pela tampa de cima quanto pela de baixo do cilindro, temos que o fluxo é :
Usando a fórmula da densidade mais uma vez para encontrar a carga interna à Gaussiana:
Mas ainda não obtivemos o campo entre as duas placas planas. Este é o campo de uma placa somente. O campo das duas é simplesmente o dobro:
Passo 4
Como encontramos um campo uniforme, aplicamos a integral para encontrar a diferença de potencial:
Como escolhemos um caminho retilíneo de uma placa para outra, o resultado da integral é simplesmente a distância entre as placas:
Passo 5
Substituindo tudo na fórmula da capacitância, temos:
E acabou!
Resposta
Exercício Resolvido #5
USP-P1-2014-Questão 4
Um cilindro condutor de comprimento e raio , com carga , é coaxial a uma camada cilíndrica condutora maior, com raio interno e carga . Despreze efeitos de borda.
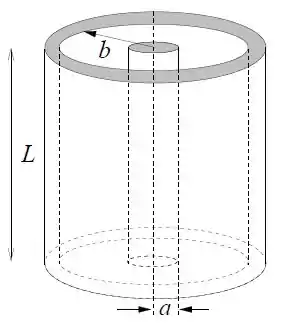
Calcule a capacitância do sistema.
Passo 1
Calcule a capacitância do sistema.
Se você nunca viu isso antes, pode parecer o tipo de coisa que você olha e fala: “Say whaaat?!”. Mas não tema, estamos aqui pra isso, não é nenhum bicho de sete cabeças.
Vamos seguindo o raciocínio lógico, ok?
Por definição, a capacitância é dada por:
Então temos que começar calculando o módulo do potencial .
Passo 2
Por definição:
Agora vamos voltar para a capacitância:
Resposta
Exercício Resolvido #6
Elaboração Própria
Considere um cilindro maciço condutor de raio e comprimento que é concêntrico com uma casca cilíndrica condutora de raios interno e externo e respectivamente e de comprimento também. A casca tem densidade linear de carga ao passo que o cilindro tem densidade linear de carga . Calcule a capacitância do sistema.
Passo 1
Pela fórmula da capacitância:
Vamos primeiro trabalhar com o módulo da voltagem. Pela fórmula, nós temos:
Agora o papo é achar o campo elétrico que esse cilindro produz.
Passo 2
Enunciando a Lei de Gauss:
Basta dividir a carga interna pela constante dielétrica . Pela simetria cilíndrica do problema, escolhemos uma Gaussiana cilíndrica de raio arbitrário e comprimento arbitrário . Dado que escolhemos uma superfície com essas dimensões e já aproveitamos a simetria do campo, temos que os vetores normais à parte lateral da superfície são paralelos ao campo, ao passo que os vetores normais nas tampas são perpendiculares à ele, de forma que:
Passo 3
Pela configuração do campo, o seu módulo é constante em toda parte lateral da Gaussiana:
E temos então a área da lateral com nossa integral:
A expressão para a área lateral é dada pela fórmula:
Logo, temos:
Coisa mais fácil do mundo é você esquecer uma letra nessa sopa... Felizmente, apesar de dar um resultado um bocado diferente, isso não costuma acarretar numa perda grande de pontos. Continuando...
Passo 4
Conforme já cansamos de saber, o quanto de carga lá dentro está relacionado com a densidade, pois a distribuição de cargas é contínua. Temos uma densidade linear constante, portanto é válido dizer que a razão entre a carga interna à Gaussiana e o comprimento dela é igual à densidade:
Logo temos:
Substituindo na expressão do campo:
Passo 5
Agora a parada é achar a diferença do potencial:
Onde o vai ser um caminho radial entre os dois cilindros. Resolvendo:
Como:
Então:
Passo 6
Substituindo tudo de volta:
Agora a parada é achar a carga do capacitor. Conectamos com a densidade, certo?
Neste momento percebemos que não vamos conseguir nos livrar do ... Isso é um fato da vida. Aqui estamos mostrando como você faria numa resolução de prova, então não teria como ver isso de antemão. Vamos ter que dar essa volta mesmo...
Enfim, terminamos!
Resposta
Exercício Resolvido #7
USP-P1-2011-Questão 4 [Modificada]
Um capacitor é formado por uma esfera condutora de raio e uma casca esférica condutora de raio , conforme a figura.
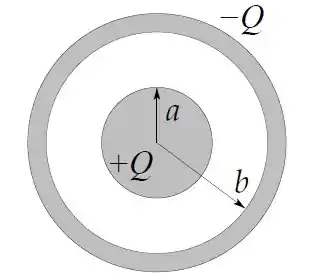
A esfera interna tem carga e a casca esférica tem carga . As respostas devem ser dadas apenas em termos de , , e .
Determine a diferença de potencial entre a esfera interna e a casca esférica.
Calcule a capacitância
Passo 1
Determine a diferença de potencial entre a esfera interna e a casca esférica.
Pra calcular a diferença de potencial ente a esfera interna e a casca esférica, podemos começar calculando o campo elétrico através da Lei de Gauss e depois encontrando a diferença de potencial usando a equação:
Eu escolhi nesse sentido por que , já que o campo tem que apontar de dentro pra fora (lembrando que o campo aponta pra direção em que o potencial diminui)
A Lei de Gauss é dada por:
A partir da simetria esférica do problema, podemos simplificar a Lei de Gauss para:
Onde é a área da nossa gaussiana esférica:
Como estamos analisando a região entre a esfera interna e a casca esférica, . Assim, a carga que está dentro da nossa gaussiana é somente a carga da esfera.
Logo:
Passo 2
Agora que calculamos , podemos calcular a diferença de potencial:
Lembrando que
Passo 3
Calcule a capacitância e determine a energia eletrostática armazenada no capacitor.
Opa! Agora que acabamos de calcular a diferença de potencial, para calcular a capacitância, basta usar a equação:
Portanto:
Simplificando esse cara:
Resposta
Exercício Resolvido #8
Elaboração Própria
Considere uma esfera condutora maciça de raio que é concêntrica com uma casca esférica condutora de raios interno e externo e respectivamente. A esfera maciça possui carga ao passo que a casca possui carga total . Calcule a capacitância desse sistema.
Passo 1
Mesma ideia de sempre. Pediu-se a capacitância então vamos partir da sua fórmula:
Como a carga que está no capacitor foi dada como , não vamos mexer com isso. Vamos apenas nos preocupar em achar o módulo da diferença de potencial entre as esferas. O módulo da ddp é quantificado por:
Que sai da fórmula da integral:
Integrando ao longo de um caminho radial entre as esferas. Para isto precisamos do campo elétrico.
Passo 2
Enunciando a Lei de Gauss...
Pela simetria esférica do problema, escolhemos uma superfície esférica de raio arbitrário para ser nossa Gaussiana . Dessa forma, os vetores normais são paralelos ao campo em todos os pontos de , do que segue o fato:
Passo 3
Além disso, pela configuração do campo, temos que o seu módulo é constante em toda , do que segue o fato:
Da última equação, segue que a integral de em toda é a área da Gaussiana. A área superficial de uma esfera é conhecida e é igual à:
Substituindo na Lei, temos:
Passo 4
Como a carga interna à Gaussiana é a carga total da esfera maciça:
Substituímos. Além disso, sabemos que o campo é radial:
Colocando na integral, temos:
E o nosso caminho vai da superfície da esfera maciça até a superfície interna da casca esférica:
Como temos que:
Então segue que:
Pode parecer uma análise desnecessária, mas mata você na múltipla escolha.
Passo 5
Podemos arrumar um pouco mais a voltagem pra substituir na fórmula da capacitância:
Substituindo:
E voilá: