Potencial Elétrico de Corpos Extensos
Produzido por Bruno SoaresTeoria
E ai? Beleza, nós somos o RespondeAi, e fazemos de tudo para você mandar bem na sua prova de Física da faculdade. No tópico de hoje estaremos interessados em entender como calcular o Potencial Elétrico Gerado por Corpos Extensos! Então vamos começar lembrando o que é Potencial Elétrico e como fazemos para calcular ele na faculdade.
Teoricamente temos que, o potencial a uma dada distância
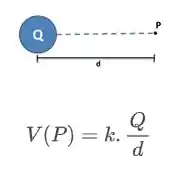
Mas para calcular o potencial elétrico de um corpo extenso precisamos calcular a carga elétrica de cada partícula que faz parte do objeto, e não de apenas uma delas. Nem sempre isso é uma tarefa fácil, porque alguns detalhes dependem da forma do objeto, mas em todos os casos vamos ter que usar nossos conhecimentos de calculo diferencial para descobrir esses potencias elétricos.
Como um exemplo vamos calcular o potencial elétrico de uma barra reta sobre o eixo
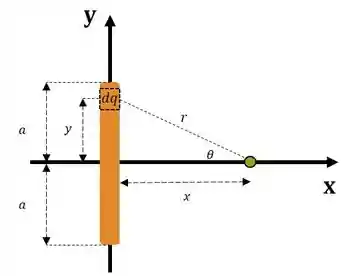
Na maioria das questões que tivermos que calcular o potencial elétrico gerado por um corpo extenso, será dito para você que a carga está uniformemente distribuída sobre o corpo e apesar de muitos relevarem essa informação ela é importantíssima. Porque a maneira em que as cargas estão distribuídas sobre o corpo, influencia diretamente sobre densidade de carga de cada pedaço infinitesimal do objeto.
Com essa densidade de carga uniforme, podemos escrever que:
Que quer dizer que para qualquer pedacinho infinitesimal
Tente visualizar que a nossa ideia vai ser percorrer todo o eixo
Da relação entre a densidade de carga e os elementos infinitesimais, escrevemos:
Bom já lembramos que a fórmula de potencial elétrico é:
Mas como estamos lidando com grandezas infinitesimais, escrevemos:
E para voltarmos para
É agora que usamos a relação que tiramos da densidade de carga, quando isolamos
Sempre nesse tipo de exercício será necessário que você retire
Realizando a substituição:
Porém temos que reparar que
E finalmente chegamos na integral que define o potencial elétrico de uma barra carregada com uma distribuição de carga uniforme:
Resolvendo essa integral, avaliando para
Caso o exercício não de para você o valor de densidade de carga, você pode descobrir ele você mesmo. Mas isso só é válido por estarmos tratando de uma distribuição uniforme, então podemos escrever que:
E por isso muitos escrevem que para uma barra com distribuição uniforme de cargas, o potencial a uma distância
UFA! Esse foi fogo, e se eu te falasse, que existem raciocínios muito parecidos para um objeto com formato de Anel, para um objeto em formato de Discos e para outros tipos de objetos?
E se eu te falasse que você encontra todos esses raciocínios dentro do nosso tópico de Potencial Elétrico Geral por Corpos Extensos? E outros objetos mais bizarros ainda dentre os exercícios resolvidos pela nossa equipe de Experts? Sei que a matéria não é simples, mas vamos seguir firme e forte na faculdade com o conteúdo do RespondeAi que foi feito especialmente pensando em você!
Exercício
Aproveita e mergulha de cabeça nesse vídeo com menos de 10 minutos que traz para você uma resolução de uma questão de prova da PUC-Rio, onde o enunciado pede para calcular o potencial elétrico de um anel não condutor:
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P1-2010.1-Múltipla Escolha n°4.
A figura à seguir mostra esquematicamente uma seção transversal de um objeto condutor maciço (de carga elétrica total nula) colocado em um campo eletrostático externo, após atingido o equilíbrio eletrostático.
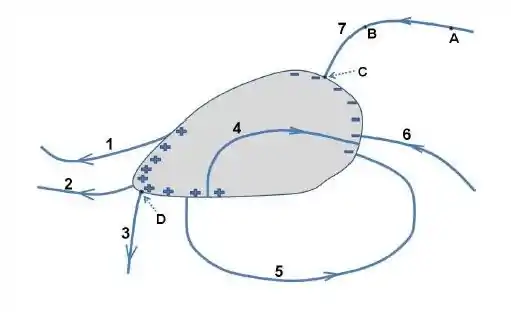
Algumas das linhas de campo elétrico, parcialmente desenhadas na figura, estão erradas e não podem corresponder a uma situação física real. Assinale a seguir cada linha impossível.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
[Atenção: nesta questão pode haver mais de um item correto].
Passo 1
Ok então. Vamos analisar as linhas de campo desta batata uma por uma, só que antes vamos estabelecer alguns critérios que impossibilitariam uma linha de campo de existir numa situação de equilíbrio eletrostático:
-
Não podem haver linhas de campo dentro do objeto condutor em equilíbrio eletrostático;
- Pois isto implicaria em ter cargas em movimento dentro dele.
- Caso contrário haveria uma componente tangente à superfície, o que implicaria nela não ser uma superfície equipotencial (algo obrigatório no equilíbrio eletrostático)
- Caso contrário ela não seria uma superfície equipotencial.
Passo 2
Passando nosso crivo por cada uma das linhas de campo:
- A primeira linha desobedece nosso segundo critério.
- A segunda linha de campo está Ok.
- A terceira está Ok.
- A quarta, por outro lado, desobedece claramente nosso primeiro critério.
- A quinta claramente desobedece nosso terceiro critério.
- A sexta está Ok.
- A sétima está Ok.
Resposta
Letras ‘a’, ‘d’ e ‘e’.
Exercício Resolvido #2
Halliday, Resnick David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 101-24.
Uma barra de plástico com uma carga uniformemente distribuída tem a forma de um arco de circunferência de raio e um ângulo central . Com no infinito, qual é o potencial elétrico no ponto , o centro de curvatura da barra?
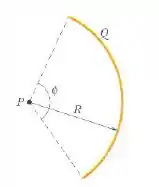
Passo 1
Escrever a contribuição infinitesimal de cada ponto do arco de circunferência para o potencial elétrico no ponto
Passo 2
Integrar as contribuições do passo anterior.
Note que o ângulo não foi importante na determinação do resultado.
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 107-104.
A figura abaixo mostra três arcos de circunferência não-condutores de raio .
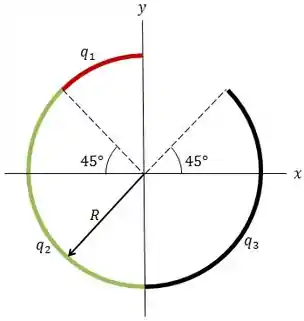
As cargas dos arcos são , e . Com no infinito, qual é o potencial elétrico dos arcos no centro da curvatura?
Passo 1
Como nós possuímos três arcos carregados, o potencial resultante será a soma dos potenciais. Então temos que calcular o potencial de cada um desses arcos.
O fato de serem arcos pode acabar te deixando na dúvida. Mas relaxa, é mais simples do que parece.
Vamos supor que a gente não saiba como resolver o problema e achássemos que íamos ter que pensar na distribuição de carga.
O procedimento aqui consistiria em pegar o potencial de uma carga pontual do corpo no centro e integra-lo no corpo todo. Como essa carga é infinitesimalmente pequena se comparada ao corpo, nós montamos a integral assim:
Assim, como o raio é constante, o potencial de cada arco será dado por:
Portanto:
Viu? Não precisa se preocupar com as distribuições, já que a distância de qualquer elemento infinitesimal para o centro vai ser sempre . Então não tem porque se preocupar.
Vamos adiante.
Passo 2
Como eu falei antes, o potencial resultante será a soma dos potenciais. Sendo assim:
Onde e .
Onde:
;
;
;
Logo:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 8º ed. Rio de Janeiro: LTC , 2008, pp 101-25 – Modificada
- A figura a seguir mostra uma barra não-condutora de comprimento e densidade linear de cargas positiva uniforme . Tome no infinito.
- A figura mostra uma barra idêntica à do item , exceto pelo fato de que a metade direta agora está carregada negativamente;
Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
O valor absoluto da densidade linear de cargas continua a ser em toda a barra. Com no infinito, qual o valor de no ponto ?
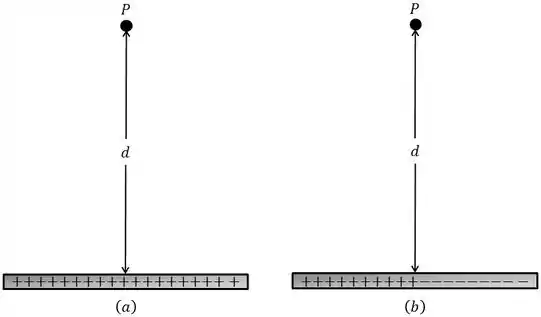
Passo 1
- Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
- Para a figura , qual o valor de no ponto ?
Como a barra é uniformemente carregada, o procedimento aqui consiste de pegar o potencial de uma carga pontual do corpo no ponto e integra-lo no corpo todo.
Como essa carga é infinitesimalmente pequena se comparada ao corpo, nós montamos a integral assim:
Passo 2
É sempre bom analisar graficamente isso para poder montar a integral corretamente.
A ideia é basicamente essa:
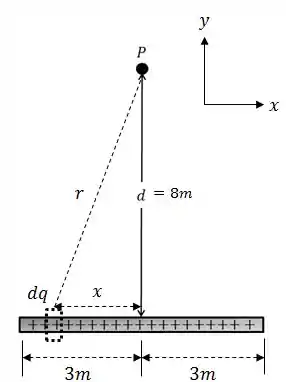
Daqui podemos tirar algumas conclusões... a primeira é que pode ser escrito como:
Outra coisa que podemos tirar daqui é: como a barra é uniformemente carregada, nós podemos usar a densidade linear de carga pra tentar facilitar a nossa vida:
Substituindo na expressão que encontramos para o potencial:
Basicamente, a questão sobre potencial já acabou, o problema agora é resolver essa integral escrota.
Vou colocar logo pra você a resposta dessa integral.
Onde:
;
;
;
Partiu!
Passo 3
Bom, antes de começar a esquentar a cabeça, vamos dar uma olhada na simetria do problema.
Como metade da barra é positiva e a outra metade é negativa, vamos pegar dois pontos simétricos em relação ao centro, com cargas de módulo , e ver como se comporta o potencial no ponto .
Graficamente, a ideia é basicamente essa
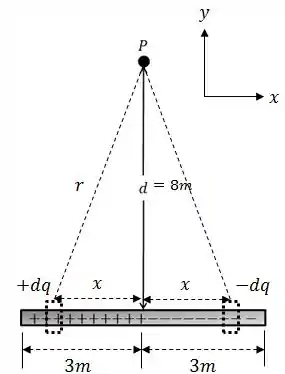
O potencial resultante desses dois elementos de carga, vai ser a soma dos dois potenciais. Portanto:
Eita! Se isso é verdade para quaisquer dois pontos simétricos, isso vai acontecer para toda a barra.
Portanto:
É razoável pensar também que, como as duas metades são iguais, mas com cargas de sinais opostos e como o potencial elétrico é uma grandeza escalar e não vetorial, as duas metades vão produzir o mesmo potencial, em módulo, no ponto , mas de sinais opostos.
Assim, quando for somar as duas, o resultado vai ser nulo.
Resposta
- ;
- ;
Exercício Resolvido #5
UFRJ-P1-2010.1-D2
Um fio retilíneo fino, de comprimento , está postado ao longo do eixo cartesiano , com seu centro na origem desse. A densidade linear de carga de tal fio é dada por:
Onde .
- Calcule o potencial eletrostático para um ponto arbitrário no eixo cartesiano , com ordenada . Faça, como usual, o potencial igual a zero no infinito [Sugestão: lembre-se que, para temos simplesmente ao passo que para temos ].
- Calcule, agora, a componente do vetor campo elétrico em tal ponto;
- Determine, por fim, a carga total de tal fio.
Passo 1
Bom, como ele pediu o potencial primeiro, eu acho mais jogo calcularmos somando potenciais infinitesimalmente pequenos de cada partícula do fio no ponto com . Então partiu:
Temos que a fórmula do potencial infinitesimal é:
Passo 2
Trocando o diferencial das cargas pela fórmula da densidade:
O diferencial é pois o fio está ao longo de :
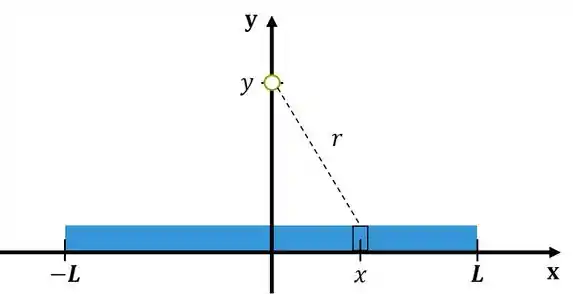
Substituindo:
Botando a densidade:
Passo 3
Pelo desenho tiramos que:
Analogamente tiramos os limites de integração:
Arrumando na vida:
Passo 4
Substituindo a fórmula da densidade:
Como estamos integrando no intervalo temos tanto negativo quanto positivo. Substituindo a definição do módulo de :
Arrumando mais:
Passo 5
A integral nós matamos com substituição simples:
Resolvemos a indefinida:
Então segue que:
Como , então , assim
Ufa. Portanto temos nosso potencial! Se você quiser substituir a constante , a resposta vai ficar:
Passo 6
Continuando, nós desejamos calcular a componente do campo elétrico. Dado que nós temos o potencial, achar o campo é moleza para fórmula abaixo:
Que é o operador de derivadas parciais. Portanto a componente vai ser o potencial derivado com relação a com sinal trocado:
Vê se não me esquece de trocar o sinal pfv! Partiu derivar:
Temos então:
E
O nosso campo ficará
Se quiser substituir o valor de , a resposta fica:
Passo 7
Para obter a carga total basta integrar a densidade na barra toda:
Manipulando a função módulo:
Resposta
Exercício Resolvido #6
UFRJ-P1-2014.1-D2
Dois anéis circulares, de mesmo raio , perpendiculares ao eixo , tem seus centros em e . Ambos possuem a mesma carga total , uniformemente distribuída.
- Determine o potencial elétrico devido aos anéis, em um ponto genérico do eixo , com abscissa , tomando tal potencial como zero no infinito ().
- Usando o potencial do item (a), determine o campo elétrico devido aos anéis, no mesmo ponto supracitado.
- Considere agora uma partícula de carga , ainda no mesmo ponto supracitado. Determine a energia potencial associada à interação dessa partícula com o campo elétrico produzido pelos anéis!
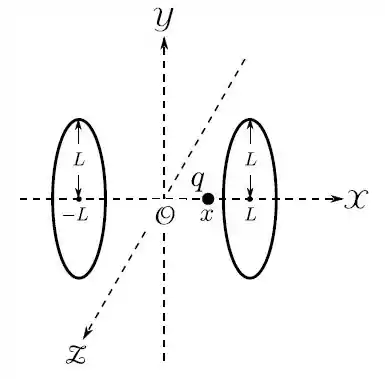
Passo 1
Como estamos tratando de anéis, a boa aqui é integral do potencial infinitesimal:
A expressão para ele nós temos da carga pontual:
Vamos fazer integrais separadas para cada anel. Para o de centro em temos:
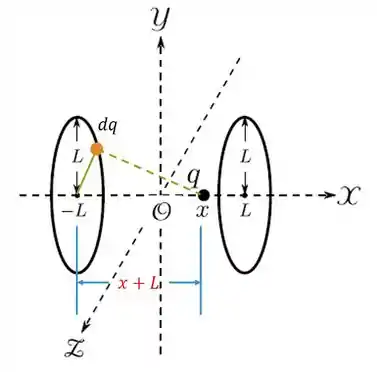
Passo 2
Como o triângulo verde é retângulo no vértice em que está , jogamos o Pitágoras:
Note como a distância é a mesma para todos os pontos do anel. Isso facilita a integral demaaaaais:
Se você se sentir mais confortável mostrando isso matematicamente, fique à vontade. Basta mostrar que o não está em função de .
Passo 3
Integrando infinitesimais em todo o anel obtemos a carga total deste:
Pela mesma lógica fazemos para o anel de centro em . Neste caso temos:
O potencial total é só a soma dos potenciais:
Fim de papo.
Passo 4
Dado que temos o potencial, achar o campo é moleza!!! Basta usar a fórmula do bem:
Onde o triangulo de cabeça pra baixo é o nosso operador de derivadas parciais:
Fazendo isso para o potencial, temos:
Passo 5
Já as outras derivadas, graças à Deus, dão zero pois o potencial não depende de nem de :
Logo:
Passo 6
Temos que a definição de potencial elétrico é a de energia potencial por unidade de carga, portanto:
Se quisermos a energia potencial basta multiplicar pela carga o potencial:
Morreu? = ]
Resposta
a)
b)
c)
Exercício Resolvido #7
PUCRIO-P1-2015.1-2
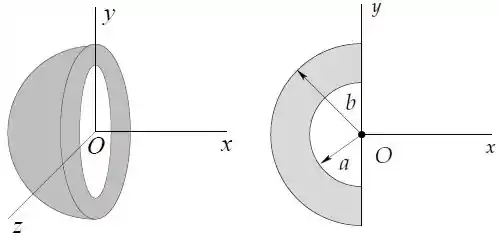
Considere um anel não-condutor situado no plano de raio interno e raio externo com uma densidade superficial de carga uniforme , como pode ser observado na figura.
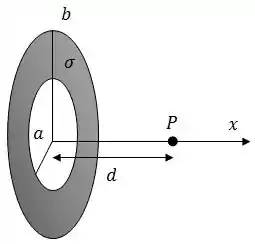
Calcule o potencial elétrico gerado por esta distribuição no ponto , a uma distância sobre o eixo indicado na figura.
A partir do resultado do item , encontre o campo elétrico (modulo, direção e sentido) no ponto .
Calcule o trabalho realizado para trazer uma carga puntiforme do infinito até o ponto .
Passo 1
Calcule o potencial elétrico gerado por esta distribuição no ponto , a uma distância sobre o eixo indicado na figura.
Vamos começar considerando um potencial gerado por um pedaço infinitesimal do disco de carga , de forma que:
Assim, o potencial será dado por:
Pra diferenciar a distância ao ponto e o raio do disco, vamos chamar o raio do disco de , beleza?
Continuando...
A áera do disco é dada por , logo, .
Graficamente, a ideia é essa:
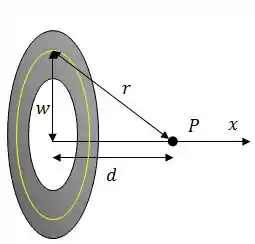
Onde:
Substituindo de volta na expressão de :
Passo 2
Pra finalizar, só temos que integrar esse cara em relação a , onde :
Essa é uma integral que não é difícil de resolver, mas que você não precisa se preocupar, porque a resposta dela provavelmente vai estar no seu formulário, então é só dar uma olhada.
Substituindo os limites de integração:
Passo 3
A partir do resultado do item , encontre o campo elétrico (modulo, direção e sentido) no ponto .
Antes de começarmos a pensar nas contas, vamos dar uma olhada na geometria do problema... pegando dois pontos equidistantes do ponto , vamos ver o que acontece com o campo elétrico.
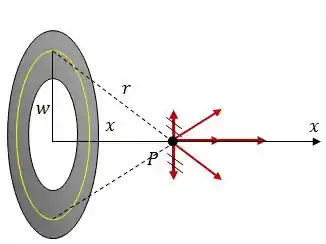
Como podemos ver, campo elétrico vai sempre se cancelar na direção paralela ao plano do disco, isso significa que temos apenas campo elétrico no sentido .
Utilizando o resultado da letra , o potencial elétrico em um ponto a uma distância do disco é:
Por definição:
Portanto:
Finalmente, o campo elétrico em um ponto a uma distância do disco é:
No ponto , , logo:
Passo 4
Calcule o trabalho realizado para trazer uma carga puntiforme do infinito até o ponto .
Essa é a mais tranquila... por definição:
No infinito . Portanto:
Substituindo a expressão de que encontramos na letra :
Resposta
Exercício Resolvido #8
PUCRIO-P1-2013.2-3
A figura ilustra uma coroa circular disposta no plano , centrada na origem, de raio interno e raio externo . Sua carga está uniformemente distribuída e possui . Use ou .
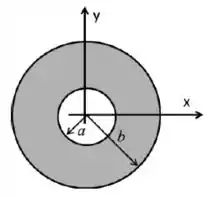
Considerando a referência para potenciais no infinito, encontre o valor do potencial elétrico num ponto qualquer do eixo , à distância da origem.
Calcule o potencial no ponto e o valor do trabalho realizado pela força eletrostática no deslocamento de uma carga teste desde até o ponto onde o potencial vale .
Suponha que o potencial gerado pela coroa circular no ponto tenha valor . Queremos anular o potencial em , e para isso dispomos de uma carga pontual de valor . Determine todos os pontos do espaço em que podemos posicionar a carga de modo a tornar nulo o potencial em .
Passo 1
Para determinar o potencial a uma distancia qualquer da origem, vamos começar com o potencial produzido por uma carga infinitesimal:
Onde , e é a distância entre cada carga e o ponto logo . Substituindo:
Integrando:
Essa linda #sqn integral é dada! Uffaa!!
Passo 2
Para o ponto em questão, teremos o seguinte potencial:
Para uma carga de prova , o trabalho para leva-la do ponto para o ponto será dado pela seguinte relação:
Passo 3
Como queremos que no ponto , o potencial seja nulo, o potencial gerado pela carga em deve ser igual em módulo ao potencial que já existe, e deve ser negativo para anular o potencial, ou seja:
O potencial gerado por uma carga é dado por:
Onde é a distância do ponto a carga, e é exatamente isso que queremos descobrir. Igualando as duas equações:
Logo, podemos colocar a carga em qualquer ponto do espaço que diste do ponto . Esses pontos formam uma esfera de raio centrada no ponto !
Resposta
Os pontos formam uma esfera de raio centrada no ponto .
Exercício Resolvido #9
USP-P1-2012-2.
Considere um disco de raio carregado uniformemente com carga . Calcule o potencial elétrico ao longo do eixo a uma distancia do centro do disco. Adote potencial nulo no infinito.
Calcule o potencial elétrico no ponto com coordenadas devido a um cilindro de altura e raio de base , uniformemente carregado com densidade volumétrica de carga . A base do cilindro está contida no plano e seu eixo coincide com o eixo , conforme a figura. Sugestão: Decomponha o cilindro em discos elementares de altura e utilize o resultado do item (a).
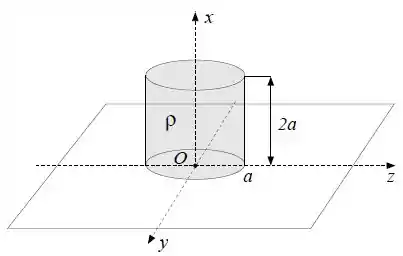
Passo 1
Considere um disco de raio carregado uniformemente com carga . Calcule o potencial elétrico ao longo do eixo a uma distancia do centro do disco. Adote potencial nulo no infinito.
Vamos começar calculando o potencial de um elemento infinitesimal do disco.
Vamos aproveitar a simetria cilíndrica do problema e dizer que esses elementos infinitesimais de carga são anéis muito finos. Assim, podemos dizer que:
Agora já podemos calcular o potencial. Substituindo isso na expressão de , arrumando e integrando esse cara, temos o seguinte:
Não tem motivo pra ficar nervoso... essa é uma integral que costuma aparecer bastante, então a resposta dela provavelmente está no formulário da prova.
Passo 2
Calcule o potencial elétrico no ponto com coordenadas devido a um cilindro de altura e raio de base , uniformemente carregado com densidade volumétrica de carga . A base do cilindro está contida no plano e seu eixo coincide com o eixo , conforme a figura. Sugestão: Decomponha o cilindro em discos elementares de altura e utilize o resultado do item (a).
Decompondo o cilindro em discos de altura e carga , o seu potencial pode ser escrito como:
Como o cilindro possui densidade volumétrica de carga , podemos usar essa densidade para encontrar uma expressão para :
Para descobrir o potencial total do cilindro no ponto , temos agora apenas que integrar esse cara:
Essa integral que aparece agora:
É outra integral dessas que você olha, fica nervoso, mas antes de surtar, tem que dar uma olhada no formulário pra ver se a integral está por lá, beleza?
Voltando ao problema:
Substituindo os valores:
E finalmente!
Resposta
Exercício Resolvido #10
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 99-7.
Uma placa condutora infinita possui uma densidade superficial de cargas
(a) Qual é o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga é deslocada da superfície da placa para um ponto situado a uma distância da superfície da placa?
(b) Se o potencial elétrico é definido como sendo zero na superfície da placa, qual é o valor de no ponto ?
Passo 1
O campo elétrico gerado por uma placa condutora infinita é uniforme, constante e possui módulo igual a:
Assim, a força elétrica que atua sobre a carga é constante e vale:
Passo 2
Quando a carga positiva parte da placa e se afasta dela, no sentido de repulsão, ela está se deslocando no mesmo sentido da força. Por isso o trabalho é positivo. Como a força atua na mesma direção do deslocamento, o trabalho seria o produto entre a força e a distância:
Passo 3
O trabalho da força elétrica se relaciona com a variação de potencial por
Definindo
Resposta
(a)
(b)
Exercício Resolvido #11
USP-P1-2012-3 - Modificada
O eixo de um cilindro condutor de de raio dista do plano conforme a figura. O cilindro é infinito na direção perpendicular ao plano da figura e todo o semiespaço é preenchido com um material condutor.
O potencial eletrostático num ponto de coordenadas no espaço fora dos condutores é dado por
onde e são em metros.
Determine o potencial no ponto do eixo do cilindro condutor .
Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.
Passo 1
Determine o potencial no ponto do eixo do cilindro condutor .
O potencial que o exercício nos deu é
Só que esse potencial só serve pra região FORA dos condutores!
Mas tem um macete aqui! Lembra que o potencial dentro de condutores tem que ser constante (já que o campo elétrico no seu interior é nulo)? Então isso significa que o potencial na borda do cilindro é igual ao potencial no seu centro, ou seja
Então pra calcular o potencial no centro do cilindro, basta calcular o potencial no ponto .
Olhando a figura as coordenadas do ponto são . Substituindo essas coordenadas no potencial temos
Assim o potencial no ponto será
Passo 2
Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.
Por definição:
Onde:
Pra descobrir cada componente do campo elétrico, temos que derivar parcialmente em função de cada uma das coordenadas e .
Por fim, o problema pede pra calcular também o campo no interior dos condutores... aí tem um detalhe que você jamais pode esquecer: o campo elétrico no interior de um condutor é sempre nulo!
Resposta
Fora dos condutores
Dentro dos condutores
Exercício Resolvido #12
USP-P1-2013-2.
Uma camada semiesférica isolante de raio interno e externo tem uma densidade volumétrica de carga que decresce com o inverso da distância ao centro segundo .
Dados e .
- Determine a carga total da camada semiesférica.
- Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
- Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?
Passo 1
- Determine a carga total da camada semiesférica.
- Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
- Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?
Beleza! O problema já nos dá a densidade volumétrica de carga
Por definição, a densidade volumétrica de carga é cada por:
Portanto, a carga total é dada por:
O elemento de volume é dado por
Onde é a área da semiesfera.
Lembrando que o raio varia entre e . Logo:
Por fim:
Passo 2
A definição de potencial elétrico diz que:
Como vimos no passo 1:
Substituindo na equação de :
Passo 3
Pra esse tipo de questão, o segredo é utilizar a conservação de energia.
Quando a carga está no ponto , ela possui energia potencial dada por:
Como já calculamos no item anterior, a energia potencial será:
No instante em que a carga é solta, ela possui apenas energia potencial, e não energia cinética.
Depois que a carga é solta, no infinito, toda essa energia potencial é transformada em energia cinética. Assim, de acordo com a conservação de energia, teremos:
Resposta
Exercício Resolvido #13
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 100-13.
Determine (a) a carga e (b) a densidade superficial de cargas de uma esfera condutora de de raio cujo potencial é (tomando no infinito).
Passo 1
Lembrar que o campo elétrico gerado por uma esfera condutora nas regiões localizadas fora da esfera possui uma fórmula muito parecida com a clássica lei de Coulomb para corpos puntiformes:
Passo 2
O potencial do campo elétrico de é constante tanto na superfície da esfera condutora quanto em seu interior e isso ocorre porque não há campo elétrico dentro da esfera, apenas na superfície dela.
Esse campo pode ser calculado por meio da integral:
Passo 3
Logo, a carga vale:
Passo 4
Para acharmos a densidade superficial, basta dividir a carga pela área da esfera:
Resposta
(a)
(b)
Exercício Resolvido #14
Elaboração Própria
Dado uma esfera condutora de raio e carga envolta por uma casca esférica condutora neutra de raios interno e externo iguais a e . Dado que o potencial no infinito é nulo, calcule o potencial em cada região:
Passo 1
Como estamos com um problema de achar o potencial de uma distribuição de cargas que aparentemente morre com Lei de Gauss, vamos preferir usar a fórmula:
Escolhendo um caminho radial, porque é mais fácil de fazer a conta. Afinal, o caminho não importa, certo?
Então a primeira coisa é achar o campo em todas as regiões. Fazendo a Lei de Gauss...
Pela simetria esférica do problema, escolhemos uma superfície esférica de raio arbitrário para ser nossa Gaussiana . Dessa forma, os vetores normais são paralelos ao campo em todos os pontos de , do que segue o fato:
Passo 2
Além disso, pela configuração do campo, temos que o seu módulo é constante em toda , do que segue o fato:
Da última equação, segue que a integral de em toda é a área da Gaussiana. A área superficial de uma esfera é conhecida e é igual à:
Substituindo na Lei, temos:
Passo 3
Vamos matar todas as regiões então. Na região , temos a parte maciça de um condutor, portanto:
Na parte de estamos fora da esfera, logo a carga total é :
Na parte em que estamos dentro da casca esférica. Só que como ela é condutora, não temos campo:
Já na região é só ver o quanto de carga total nós temos, que no caso é só proveniente da esfera:
Portanto:
Passo 4
Agora vamos fazer a conta partindo de um lugar cujo potencial nós conhecemos. No caso o enunciado nos deu o potencial no infinito, então vamos começar nosso caminho partindo de lá para algum ponto em que :
Plugando o campo correspondente à região na equação:
Que resulta em:
Ou seja, mesma coisa que a carga pontual.
Passo 5
Agora vamos partir para a região , que tem outra expressão do campo elétrico. A parada é partirmos de um ponto onde conhecemos o potencial, mas como obtivemos a expressão do potencial no passo anterior, podemos usá-la.
CUIDADO com os limites de integração! Plugando o campo e o potencial conhecidos:
Fazendo:
Logo:
Passo 6
Partindo agora de um ponto na superfície em que vamos para a região . O potencial nesse ponto é só substituir na expressão encontrada anteriormente, ou perceber que não depende de :
Logo, integramos novamente:
Passo 7
Mesma coisa, só que agora partindo da superfície , e vamos para :
Resposta
Exercício Resolvido #15
Elaboração Própria
Um cilindro condutor infinito ao longo do eixo de raio tem densidade de carga constante . Calcule o potencial a uma distância do eixo do cilindro, dado que a uma distância ele vale . O potencial dado poderia ter sido no infinito?
Passo 1
Rascunhando a situação, temos:
Como essa questão é a cara da Lei de Gauss para calcular o campo, vamos preferir utilizar a fórmula:
Escolhendo um caminho radial em direção ao cilindro. Estabelecido isso, vamos partir para calcular o campo. enunciando a Lei de Gauss:
Pela simetria cilíndrica do problema, escolhemos uma Gaussiana cilíndrica de raio arbitrário e comprimento arbitrário . Dado que escolhemos uma superfície com essas dimensões e já aproveitamos a simetria do campo, temos que o vetores normais à parte lateral da superfície são paralelos ao campo, ao passo que os vetores normais nas tampas são perpendiculares a ele, de forma que:
De forma que:
Portanto:
Passo 2
Pela configuração do campo, o seu módulo é constante em toda parte lateral da Gaussiana:
E temos então a área da lateral com nossa integral:
A expressão para a área lateral é dada pela fórmula:
Logo, temos:
Passo 3
Temos uma densidade linear constante, portanto é válido dizer que a razão entre a carga interna à Gaussiana e o comprimento dela é igual à densidade:
Logo temos:
Substituindo na expressão do campo:
Ainda pela questão da simetria, temos que o campo vai ter somente essa componente radial, então:
Passo 4
Partindo do ponto dado para um ponto arbitrário com distância até o centro, escolhemos um caminho qualquer.
O caminho pode sim ser qualquer um, como na figura, mas se você quiser evitar do examinador da prova exigir uma demonstração desse fato, talvez você queira particularizar e dizer que o caminho é radial, daí nesse caso temos que o campo e o seu vetor são sempre paralelos ao longo do caminho. Aplicando na fórmula, temos:
Arrumando:
E é isso. Mas e aí, poderia ter sido arbitrado no infinito esse potencial inicial? Não, pois a integral não aceitaria . Você estaria tentando fazer:
Coisa que não daria certo, pois é infinito também.