Energia Potencial Elétrica
Produzido por Bruno SoaresTeoria
Fala aí, aqui é o Responde Aí, nós somos sua salvação hahaha. Com a gente você aprende de forma rápida e descontraída e arrasa na prova!
Nosso papo hoje é sobre Energia Potencial Elétrica e algumas outras coisinhas que envolvem essa energia. Então bora lá começar!
Quando temos cargas elétricas espalhadas no espaço, há uma interação entre elas, isso porque as cargas produzem campo elétrico que se permeia no espaço, produzindo forças de atração ou repulsão nas cargas vizinhas. Quando consideramos cargas fixas no espaço, existe uma energia de interação entre essas cargas que faz com que elas fiquem exatamente onde estão. Essa energia é o que chamamos de energia potencial elétrica e ela pode ser transformada em energia cinética no caso de uma das cargas que interagem ser móvel.
Sozinha uma carga elétrica não apresenta energia potencial elétrica, é preciso que haja duas ou mais cargas interagindo, formando um sistema para que haja uma energia potencial associada.
Vamos começar com o caso mais simples: apenas duas cargas interagindo no espaço.
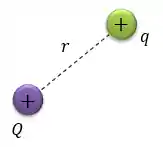
Nesse caso, a energia potencial de interação entre essas duas cargas será dada por:
Onde:
e são as cargas que estão interagindo. É o valor da carga mesmo, sem módulo, expresso em ; é a constante eletrostática. No vácuo ela vale ; é a distância entre as cargas, expressa em , e; é a energia potencial elétrica, expressa em
Mas, os professores em prova não gostam de facilitar né kkk, então costumam aparecer questões que tem mais de duas cargas interagindo, como nesse caso aqui:
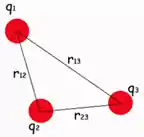
E aí, o que fazemos nesse caso? Se desesperar não é uma opção, porque você encontrou o Responde Aí.
A energia potencial elétrica é formada em cada par de cargas, então, quando temos mais de duas cargas o que temos que fazer é combinar as cargas duas a duas e somar a energia potencial elétrica que ocorre entre cada par.
Nesse exemplo nós temos os seguintes pares de cargas:
Beleza?
Uma conceito muito importante que está associado com a energia potencial elétrica é o trabalho.
É bem comum nos depararmos com questões que pedem o trabalho da força elétrica para levar as cargas, que estão interagindo, de uma configuração para outra. Esse trabalho se associa com a energia potencial elétrica da seguinte maneira:
Onde:
é o trabalho da força elétrica, e; é a diferença de energia potencial elétrica entre a configuração final e a configuração inicial.
Exemplo
Vamos fazer um exemplo aqui bem rapidinho para ficar mais claro, beleza?
Calcule o trabalho da força elétrica associado a mudança de configuração ocorrida, como mostra a figura abaixo:
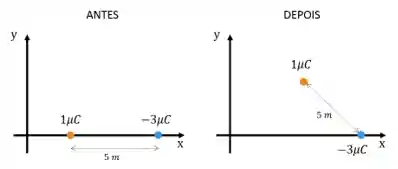
RESOLUÇÃO:
Para achar o trabalho precisamos calcular a enegia potencial elétrica antes e depois:
Obs.: Na hora de colocar o valor da carga na fórmula, ele foi muliplicado por
Agora para obtermos o trabalho que fazer a diferença de energia e trocar o sinal:
Prontinho, essa foi nossa conversa hoje. Espero te ver por aqui mais vezes 😉
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.
Uma carga puntiforme está na origem e uma segunda carga puntiforme está no eixo em . Determine uma expressão para o potencial em qualquer ponto do eixo como uma função de .
Passo 1
Vamos desenhar o que temos nesse problema, uma das cargas está na origem e a outra em e as distâncias são definidas assim
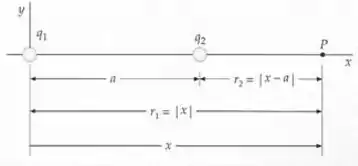
Para resolver esse probleminha, vamos lembrar que o potencial total vai ser a soma dos potenciais devido a cada carga separadamente, ou seja
Passo 2
Substituindo na expressão de o que já temos, vai ficar assim
Repare que quando ou , .
E quando , .
Resposta
Exercício Resolvido #2
Hugh D. Young e Roger A. Freedman, Física III – Eletromagnetismo, 12ª ed. São Paulo, 2010, pp. 95
Uma carga puntiforme é mantida em repouso na origem. Uma segunda carga puntiforme se desloca no ponto , até o ponto , . Qual é o trabalho realizado pela força elétrica sobra a carga ?
Passo 1
O trabalho é dado pela variação da energia potencial:
Ao passo que a fórmula da energia potencial é:
Temos a seguinte situação:
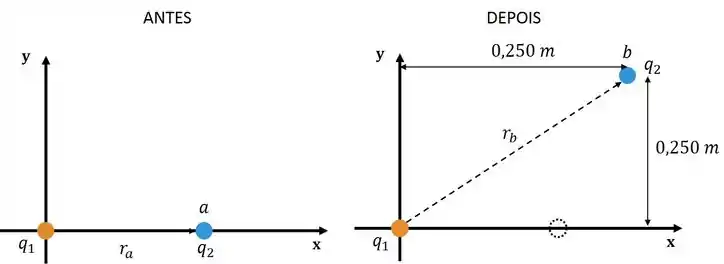
Passo 2
A posição inicial de é em e a posição final é em , portanto temos:
Passo 3
Aplicando a fórmula e substituindo os valores que conhecemos temos:
Já no ponto temos:
Passo 4
O que produz uma variação de:
Resposta
O trabalho exercido é:
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física III – Eletromagnetismo, 12ª ed. São Paulo, 2010, pp. 95
Uma carga puntiforme é mantida em repouso na origem. Uma segunda carga puntiforme é colocada em um ponto e a energia potencial elétrica desse conjunto de duas cargas é igual a . Quando a segunda carga se desloca até um ponto , o trabalho realizado pela força elétrica sobre a carga é igual a . Qual a energia potencial elétrica desse conjunto de cargas quando a segunda carga se encontra no ponto ?
Passo 1
O trabalho se relaciona com a energia elétrica pela seguinte fórmula:
Neste caso, a carga vai de para :
Passo 2
Aplicando os dados:
Isolando a quantidade pedida
Resposta
Exercício Resolvido #4
UFRJ-P1-2014.1-ME03.
Qual é o trabalho necessário para formarmos a configuração de três partículas, todas com a mesma carga , supondo que tais partículas estão, de início, infinitamente afastadas?
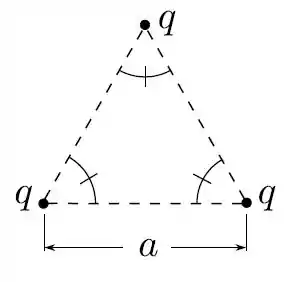
Passo 1
Perguntou o trabalho e tem um triângulo na figura! Essa questão é clássica. Para configurações discretas de cargas nós sabemos a energia potencial que elas armazenam:
E também temos a fórmula da relação entre trabalho e variação da energia potencial:
Passo 2
Vamos achar a variação da energia. No início ele disse que as cargas estão muito afastadas:
Que na fórmula vai dar que a energia potencial é zero:
E no final nós temos que as distâncias são todas iguais a e as cargas são iguais a :
Passo 3
Aplicando a fórmula, temos:
O trabalho é, portanto:
Esse seria o trabalho do campo elétrico, certo? Mas pra formar essa configuração, o trabalho é realizado por uma força externa! Como , onde é o trabalho do campo que a gente achou:
Logo...
Resposta
Letra e.
Exercício Resolvido #5
UFRJ-Pf-2014.2ME05
Qual é o trabalho necessário para formarmos a configuração das quatro partículas da figura (3 partículas positivas e uma negativa, nos vértices de um quadrado de lado ), supondo que as partículas estejam, de início, infinitamente afastadas umas das outras?
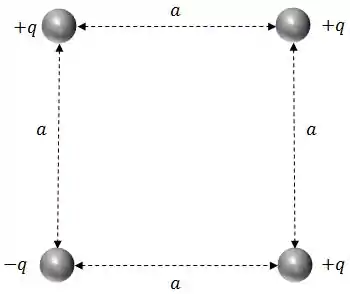
Passo 1
Vamos começar numerando esses caras, ok?
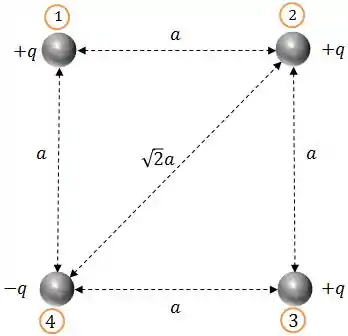
Assim, a energia total será:
Onde:
Portanto:
A resposta certa é a letra .
Resposta
Exercício Resolvido #6
Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 23, pp. 102
Três cargas puntiformes, inicialmente muito afastadas entre si, estão sobre os vértices de um triângulo equilátero, de lado igual a . Duas dessas cargas são idênticas e possuem carga . Desejamos realizar um trabalho líquido igual a zero para colocar as três cargas nos vértices do triângulo; qual deve ser o valor da terceira carga?
Passo 1
Vamos começar imaginando dois casos: caso 1, quando as cargas estão infinitamente distantes; e caso 2, quando elas estão nos vértices do triângulo, como na figura abaixo. Chamamos a terceira carga, que ainda não conhecemos, de .
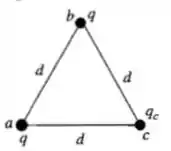
Passo 2
Agora, calculamos o trabalho realizado para que as cargas venham do infinito (caso 1) para os vértices do triângulos (caso 2). Temos que:
Sabemos que, para o caso 1, com as cargas no infinito, . Já para o caso 2, temos que:
Como queremos que , logo:
Logo, o valor pode ser calculado como:
Resposta
(a) .
Exercício Resolvido #7
UFRJ- Física 3 – P1 2017.1 - DIURNO - 5
Três partículas carregadas com cargas , e são fixadas sobre os vértices de um triângulo equilátero, como mostrado na Figura abaixo. O centro do triângulo é indicado pelo ponto .
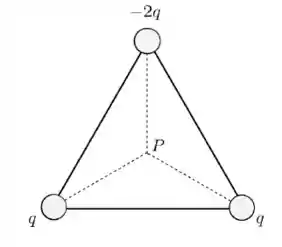
Considere que a energia potencial elétrica seja nula quando as cargas estiverem infinitamente afastadas. Sobre esse sistema, são feitas as afirmativas abaixo:
- A energia potencial elétrica do sistema é negativa.
- O potencial elétrico é constante sobre um eixo perpendicular ao triângulo e que passa por .
- O trabalho realizado pela força elétrica sobre uma partícula carregada, quando ela é deslocada do infinito até o ponto , é nulo.
São VERDADEIRAS as afirmativas:
- Nenhuma delas.
Passo 1
I) Para calcularmos a energia potencial elétrica do sistema, vamos tomar a Figura a seguir com as partículas , e com cargas e , respectivamente. A energia potencial elétrica entre duas partículas quaisquer e , separadas por uma distância , é dada por
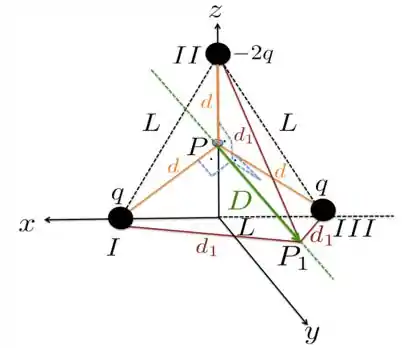
A partir dessa Figura, vamos considerar apenas os seguintes pares de partículas , e . Por quê não colocamos também o par ? Porque esta energia será idêntica àquela do par , que já foi considerada. Ou seja, só precisamos contabilizar a energia de um par uma única vez.
Tendo isso mente, pessoal, a energia potencial elétrica do sistema neste caso é
que é negativa, tornando o item desta questão CORRETO.
Passo 2
II) Como o ponto da figura está no centro do triângulo equilátero, ele está situado a uma mesma distância igual de todas as cargas do triângulo, correto?
A reta que passa pelo ponto da figura é perpendicular ao plano definido pelas três cargas e um ponto arbitrário desta reta está à mesma distância de todas as três cargas, como indicado na figura. Portanto, os triângulos , e são retângulos e iguais.
Assim, o potencial produzido pelas cargas na posição de um ponto arbitrário da reta é dado por
ou seja, o potencial em qualquer ponto sobre a reta é CONSTANTE E IGUAL A ZERO! Por isso, o item II) está CORRETO.
Passo 3
III) Como o problema se trata de um sistema de cargas estáticas, então temos um sistema conservativo. Dessa maneira, o trabalho realizado pelo campo elétrico desse sistema para levar uma partícula de carga do infinito até o ponto depende apenas da energia potencial no infinito e da energia potencial no ponto
A energia num ponto a um distância arbitrário do sistema pode ser escrita como
em que é o potencial gerado pela distribuição no ponto . Então, o trabalho pode ser escrito como
Como o potencial gerado pelo sistema no infinito é zero, , e o potencial no ponto também (o potencial sobre qualquer ponto sobre a reta é constante e nulo!), então o trabalho é
Portanto, a energia gasta pelo sistema para levar qualquer partícula do infinito até o ponto é ZERO.
O item III) da questão está CORRETO.
Resposta
Portanto, o item g) está correto.
Exercício Resolvido #8
UFRJ- Física 3 - PF 2017.2 - DIURNO - 5
Deseja-se acelerar um elétron do repouso até uma velocidade igual a da velocidade da luz. Sabendo que a massa do elétron vale , sua carga vale e a velocidade da luz vale , qual é a diferença de potencial a que ele deve ser submetido?
Passo 1
Neste problema, como o elétron estará submetido a uma diferença de potencial, uma força conservativa realizará um trabalho sobre ele e o levará de um ponto até um ponto .
Na posição do ponto , ele está em repouso e no ponto , ele terá uma velocidade bem definida e estamos interessados na diferença de potencial .
Como a força é conservativa, sabemos que o trabalho realizado sobre o elétron para levá-lo de até é dado por
em que é a energia potencial associada a cada um dos pontos e é o potencial, que é a energia por unidade de carga fornecida à partícula.
Outro fato importante é que esse trabalho é igual à variação da energia cinética do elétron. Isto é
Como a partícula carregada é um elétron, temos e temos também que , pois o elétron parte do repouso. Nesse caso, a expressão acima nos dá que
Resposta
Portanto, a resposta correta é a letra a) .